Детерміновані однопродуктові моделі оптимальної партії поставки Аналіз економічно вигідного розміру партії

При формуванні оптимальної партії поставки враховуються затримки двох типів: затримки замовлення і затримки змісту запасів . Вважається, що затримка замовлення по даному маршруту не залежить від величини партії поставки, отже, витрати на подання замовлень дорівнюють ; витрати на зберігання запасів пропорційні середній величині запасу і часу його зберігання. Якщо, наприклад, — затримка зберігання одиниці запасу, то при його рівномірному споживанні затримки зберігання протягом часу становлять , де — величина партії поставки. Враховуючи, що ( — інтенсивність споживання) при повтореннях замовлення, загальні витрати замовлення і зберігання запасів становлять Або, розділивши на отримаємо витрати за одиницю часу:

(3.1)

Звідси, прирівнявши похідну (3.1) по до нуля, отримаємо

(3.2)

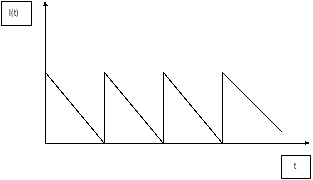
Рис.12

Динаміка зміни рівня запасів в такій моделі зображена на рис.12.

Знаючи оптимальний розмір партії поставки(замовлення), можна визначити ряд інших параметрів постачання. Частково, маємо: оптимальний інтервал між поставками

(3.3)

середній рівень запасу

(3.4)

Якщо, наприклад, деякий інтервал планування, то оптимальна кількість придбаних партій в залежності від початкового стану складає

або (3.5)

де — найбільше ціле число, що не перевищує . Сумарні витрати за одиницю часу по формуванні і зберіганні запасів при оптимальному значенні дорівнюють

(3.6)

Або, позначимо сумарне споживання за проміжок часу планування через , затримки зберігання одиниці запасу за час через , отримаємо значення оптимальних витрат за період планування:

(3.7)

Так як в рівнянні (3.1) похідні доданків є величина стала

то функція затримок (3.1) досягає мінімуму при рівності цих доданків, тобто при умові

Звідси

(3.8)

тобто при стаціонарному детермінованому попиті оптимальна партія поставки досягається при умові рівності затримок формування запасів і затримок їх зберігання.

Позначимо через відношення прийнятого розміру одної поставки до оптимального

(3.9)

Враховуючи вираз (3.9), із функціонала (3.1) отримаємо

(3.10)

Формула (3.10) показує, що незначні відхилення від оптимальної партії поставки не впливає на затримки функціонування. Наприклад, для того щоб затримки функціонування системи збільшились в 2 рази, необхідно відхилення партії поставки від оптимального розміру в рази.

Як видно з формули (3.10), відносне збільшення партії в разів. Причому при всіх значеннях . З наведеного аналізу випливає, що оптимальний розв’язок рівняння (3.2) володіє доброю стійкістю.

Розглянемо, як впливають відносні похибки в визначенні параметрів і на затримки системи.

Нехай

(3.11)

Тоді

(3.12)

Із виразу (3.9) і формули (3.12), випливає

(3.13)

Враховуючи формули (3.10) і (3.13), отримаємо

(3.14)

Аналогічно отримуємо

(3.15)

З формул (3.14) і (3.15) випливає, що похибки в визначенні параметрів і однаково впливають на затримки функціонування.

Ця обставина має незначний вплив (в деяких границях) відхилень партії поставки і похибки параметрів моделі на затримки функціонування системи зовсім не показує непотрібності використання формули оптимальної партії поставки. Скоріше, навпаки, вона підкреслює складність і актуальність проблем, що стоять перед економічною наукою по відношенню до вдосконалення методів формування необхідної інформації.

Ідеї, що лежать в визначенні економічно-вигідного розміру партії, можна застосовувати для визначення націнки складу.

Нехай оптова ціна продукції становить . Припустимо, що попит є функцією націнки складу , тобто . При таких умовах прибуток постачальницької організації становить

.

Максимальний прибуток можна знайти з рівняння

. (3.16)

розв’язок якого дає оптимальний розмір націнки складу.

На практиці зміни запасів відбуваються під впливом багатьох факторів. Щоб з найменшими витратами спрямувати розвиток всієї системи в потрібному напрямку, необхідно врахувати взаємодію цих факторів, визначити степінь впливу на затримки кожного з них.

Застосування економіко-математичних методів для виявлення пропорцій зміни запасів в залежності від основних факторів дає можливість більш точно оцінити стан запасів і перспективу їх розвитку, знайти тенденцію їх зміни.

Під загальною величиною запасу будемо розуміти суму його поточної і страхової частини. Поточним запасом називають частину загального запасу, яка призначена для забезпечення потреб виробництва при неспівпадінні термінів і розмірів поступлень і споживання матеріальних ресурсів. Страхова частина запасу призначається для забезпечення безперервного постачання матеріалами при відхиленнях інтервалів і партій доставок від передбачених при розрахунку норм поточного запасу.

Окрім моделей оптимізації процесів запасання важливу роль відіграють моделі динаміки зміни запасів. Для аналізу стану запасів, наприклад, встановлюється залежність між споживанням і середнім рівнем запасів, між середнім рівнем запасів і кількістю доставок підчас планового періоду, між кількістю доставок і величиною споживання і ін. Така залежність зазвичай встановлюється методами кореляційного або регресивного аналізу. Важливим питанням при побудові таких моделей є вибір математичної форми зв’язку, тобто аналітичної функції (рівняння регресії), що відображає сутність зв’язку між величинами, що вивчаються. Не має ніяких загальних правил, з допомогою яких можна вибрати найбільш придатну криву. При виборі форми залежності потрібно виходити з аналізу відношень між залежністю змінної і аргумента. Але найкращою є форма кривої, яка є наслідком теоретичних роздумів. Після того як вибраний і обгрунтований тип рівняння зв’язку, визначають значення параметрів. Параметри можуть бути визначені, наприклад, методом найменших квадратів.

Встановимо вид зв’язку між деякими величинами, що входять в модель управління запасами. Розглянемо зв’язок, наприклад, між загальною величиною запасу і інтенсивністю споживання. З формули Уілсона випливає

або, позначивши через , отримаємо

. (3.17)

Знайдемо залежність середнього поточного запасу, виражену в добах, від інтенсивності споживання:

.

Норма загальної величини запасу, виражена в добах, складається з суми норми страхового запасу і поточного , тобто

. (3.18)

Аналогічно можна знайти вид залежності між нормою загальної величини запасу і кількістю доставок :

; (3.19)

. (3.20)

З формул (3.19) і (3.20) випливає

,

де — плановий період. Або, враховуючи величину страхового запасу,

. (3.21)

З виразу (3.21) запишемо залежність між числом замовлень і інтенсивністю поступлень .

Модель з сталою (>0) інтенсивністю надходжень

Розглянемо класичну модель найбільш економічного розміру партії при умові, що поставки не миттєві, а визначаються сталою інтенсивністю поступлень . Динаміка зміни запасів опишеться при цьому кусково-лінійною функцією часу (рис.13).

Так як протягом часу йде збільшення запасів і їх витрата, то абсолютна інтенсивність поступлень на склад визначиться їх різницею . Звідси максимальна величина запасу

. (3.22)

При цьому запас повністю витрачається протягом . Тому

. (3.23)

Крім цього,

. (3.24)

Рис.13

З формул (3.22) — (3.23) маємо:

; (3.25)

. (3.26)

Затримки зберігання визначаються множником на площу трикутника . Повні затримки одного циклу, пов’язані з замовленням і складом, становлять

. (3.27)

Розділивши вираз (3.27) на довжину циклу , отримаємо затримки за одиницю часу:

Звідси, прирівнявши першу похідну по до нуля, знаходимо

. (3.28)

Знайдемо інші параметри, що відповідають оптимальній партії поставки.

Оптимальні окремі затримки системи

. (3.29)

Оптимальний період відновлення замовлення

. (3.30)

Оптимальний час поступлення замовлення

.

В випадку високої степені виконання запасу, тобто при , з формули (3.28) отримаємо класичну формулу оптимальної партії поставки.