5.5. Ігри порядку 2 2, 2 n та m 2. Графічне розв’язування ігор.

Матриця гри розміру 2 2 . Якщо є сідлова точка, то гра розв’язана. В іншому випадку шукаємо точку в змішаних стратеґіях , . Для оптимальності змішаних стратеґій необхідно виконання наступних співвідношень:

Якщо матрична гра не має сідлової точки в чистих стратеґіях (тобто , , , , то згідно до наслідків з теорем вищенаведені нерівності перетворюються в рівності (якщо припустити, що яка-небудь з нерівностей виконується строго, то це б означало, що відповіднва їй змінна двоїстої задачі повинна бути рівною нулю — що суперечить припущенню про відсутність сідлової точки, а самен цей випадок ми розглядаємо. Розв’язуючи системи рівнянь аналітично

, отримаємо . .

В іграх порядку 2 n гравець А має лише 2 чисті стратеґії, а В — n.

Матриця гри має вигляд .

Якщо гра не має сідлової точки, то необхідно знайти такі мішані стратеґії, для яких згідно до наслідку з теорем теорії ігор виконувалися б наступні умови:

1). 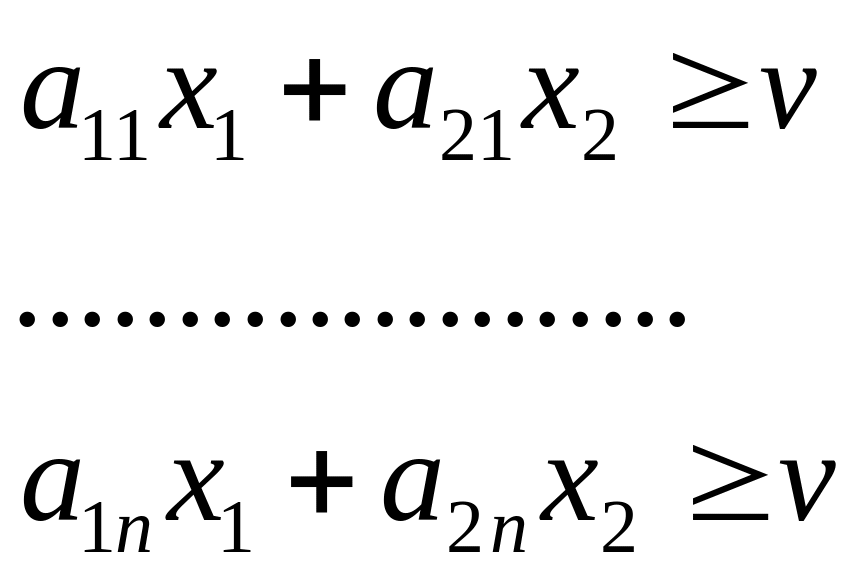2).

3). 4). .

Оскільки гра не має сідлової точки, нерівності 2-ї групи перетворяться в рівністі (якщо припустити, що хоча б одна з цих нерівностей строга, то їй мало б відповідати нульове значення x, що суперечить твердженню про те, що гра не має сідлової точки.

Таким чином необхідно розв’язати систему (1-4) за умови що група 2 — рівності. Для розв’язування використаємо ґрафічний метод. Введемо позначення для лівої частини нерівностей 1-ї групи

,

де — середній виграш гравця А, коли він застосовує змішану стратеґію , а гравець В — чисту стратеґію В_j. Гравець В прагне мінімізувати програш — тобто обрати , а гравець А — збільшити свій виграш .

Таким чином і визначається оптимальна мішана стратеґія гравця А та пара чистих стратеґій гравця В, які в перетині дають .Далі розв’язуємо систему з тими чистими стратеґіями гравця В, які знаходяться на перетині .

Приклад 5. Розв’язати ґрафічно гру, задану наступною матрицею:

.

Випишемо середні виграші гравця А при застосуванні ним мішаної стратеґії, а гравцем В — чистої для кожної з чистих стратеґій гравця В:

M₁(x₁)=(10-1)x₁+1=9x₁+1

M₂(x₁)=(8-2)x₁+2=6x₁+2

M₃(x₁)=(6-4)x₁+4=2x₁+4

M₄(x₁)=(4-3)x₁+3=x₁+3

M₅(x₁)=(2-12)x₁+12=-10x₁+12

M₆(x₁)=(3-6)x₁+6=-3x₁+6.

Зобразимо середні виграші графічно.

Найбільший виграш матиме гравець А, якщо він обере змішану стратеґію, що відповідатиме застосуванню гравцем В суміші чистих стратеґій В₄ та В₆. Звідси записуємо системи рівнянь для визначення мішаних стратеґій гравців А та В:

4x₁+3x₂=v 4y₄+3y₆=v

3x₁+6x₂=v 3y₄+6y₆=v

x₁+x₂=1 y₄+y₆=1.

Розв’язуючи, отримаємо x₁*=3/4, x₂*=1/4, y₄*=3/4, y₆*=1/4, v=15/4.

Таким чином оптимальні стратеґії гравців будуть x*=(3/4,1/4), y*=(0,0,0,3/4,0,1/4), а ціна гри v=15/4.

В іграх порядку m 2 гравець А має m чистих стратеґій, а В — 2.

Матриця гри має вигляд .

Якщо гра не має сідлової точки, то необхідно знайти такі мішані стратеґії, для яких згідно до наслідку з теорем теорії ігор виконувалися б наступні умови:

1). 2).

3). . 3).

Оскільки гра не має сідлової точки, нерівності 1-ї групи перетворяться в рівності (якщо припустити, що хоча б одна з цих нерівностей строга, то їй мало б відповідати нульове значення y, що суперечить твердженню про те, що гра не має сідлової точки.

Таким чином необхідно розв’язати систему (1-4) за умови що група 1 — рівності. Для розв’язування використаємо ґрафічний метод. Введемо позначення для лівої частини нерівностей 2-ї групи

,

де — середній програш гравця А, коли він застосовує мішану стратеґію , а гравець А — чисту стратеґію А_і. Гравець А прагне максимізувати виграш — тобто обрати , а гравець В — зменшити свій програш .

Таким чином і визначається оптимальна мішана стратеґія гравця В та пара чистих стратеґій гравця А, які в перетині дають .Далі розв’язуємо систему з тими чистими стратеґіями гравця А, які знаходяться на перетині .

Приклад 6. Розв’язати ґрафічно гру, задану наступною матрицею:

Випишемо середні програші гравця В при застосуванні ним мішаної стратеґії, а гравцем А — чистої для кожної з чистих стратеґій гравця А:

M₁(y₁)=-2y₁+4; M₂(y₁)=-y₁+3;

M₃(y₁)=y₁+2; M₄(y₁)=-8y₁+6.

Зобразимо середні виграші графічно.

Найменший програш матиме гравець В, якщо він обере змішану стратеґію, що відповідатиме застосуванню гравцем А суміші чистих стратеґій А₁ та А₃. Звідси записуємо системи рівнянь для визначення мішаних стратеґій гравців А та В:

2x₁+3x₃=v 2y₁+3y₂=v

4x₁+2x₃=v 3y₁+2y₂=v

x₁+x₃=1 y₁+y₂=1.

Розв’язуючи, отримаємо x₁*=1/3, x₃*=2/3, y₁*=2/3, y₂*=1/3, v=8/3.

Таким чином оптимальні стратеґії гравців будуть x*=(1/3,0,2/3,0), y*=(2/3,1/3), а ціна гри v=8/3.