5.3. Змішані стратегії в іграх двох осіб з нульовою сумою

Не кожна матрична гра має розв’язок в чистих стратегіях. Дослідження гри починається зі знаходження сідлової точки. Якщо сідлова точка існує, то розв’язок гри знайдений — стоп. Якщо ж ні — то можна визначити верхню та нижню ціну гри, однак така інформація недостатня.

Покращення розв’язку слід шукати в використанні секретності застосування чистих стратегій за умови багаторазового повторення гри в вигляді партій. В середньому будуть досягнуті деякі виграші, які будуть більші, ніж нижня ціна гри, та менші, ніж верхня. Чим більше це середнє значення, тим краще застосовує стратеґії гравець А. Тому виникла ідея застосовувати стратеґії випадковим чином з певною ймовірністю, що повністю забезпечує секретність їх застосування. Кожен гравець може змінювати ймовірності застосування своїх чистих стратегій, щоб забезпечити собі максимальний середній виграш.

Визначення 1. Мішаною стратеґією гравця називається повний набір ймовірностей застосування ним його чистих стратеґій. Таким чином, якщо гравець А застосовує m чистих стратеґій, то змішана стратеґія задовільняє умови: . Аналогічно змішана стратеґія гравця B : .

Визначення 2. Середній виграш гравця А в матричній грі відображається як математичне сподівання його виграшу при застосуванні ним стратеґії , а гравцем В — стратеґії , і аналогічно для гравця В:

.

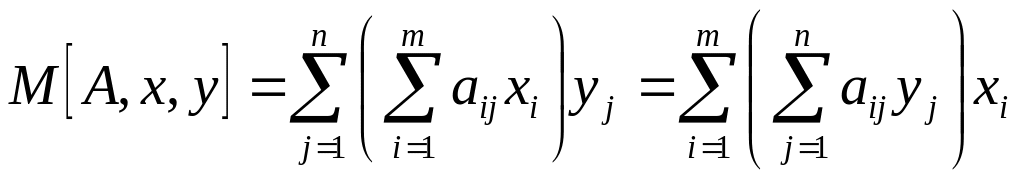У цьому випадку верхня ціна гри , а нижня — .

За аналоґією з іграми, що мають сідлові точки в чистих стратеґіях, введемо поняття оптимальних мішаних стратеґій.

Визначення 3. Оптимальними мішаними стратеґіями гравців А тв В відповідно називаються такі стратеґії та , які задовільняють рівність

.

Еквівалентним визначенням є наступне. Мішані стратеґії та є оптимальними, якщо вони утворюють сідлову точку функції , тобто

.

Визначення 4. Величина називається ціною гри та позначається .

Основна теорема теорії матричних антаґоністичних ігор двох осіб вперше була доведена Дж. фон Нейманом відповідає на питання : Чи мають матричні ігри розв’язки і які?

Теорема 3. (Основна теорема теорії матричних ігор). Для матричної гри з довільною матрицею А величини та існують завжди та є рівними між собою. Таким чином для матричної гри завжди існує розв’язок в мішаних стратеґіях.

Наступні теореми та наслідки з них дають відповідь на запитання: Яким чином знайти розв’язки матричних ігор?

Теорема 4. Для того, щоб в матричній грі з ціною змішана стратеґія гравця А була оптимальною, необхідно та достатньо, щоб для довільної стратеґії гравця В виконувалась нерівність .

Аналогічно для гравця В: для того, щоб в матричній грі з ціною змішана стратеґія гравця В була оптимальною, необхідно та достатньо, щоб для довільної стратеґії гравця В виконувалась нерівність .

Наслідок. Для того, щоб , була оптимальною мішаною стратеґією матричної гри з матрицею та ціною гри , необхідно та достатньо, щоб виконувалися наступні нерівності: , .

Аналогічно для гравця В: Для того, щоб , була оптимальною мішаною стратеґією матричної гри з матрицею та ціною гри , необхідно та достатньо, щоб виконувалися наступні нерівності: , .

Таким чином для розв’язування гри необхідно визначити стратеґії, що задовільняють вищенаведені системи обмежень та умови нормування: , .

Цей наслідок дозволяє сформулювати для розв’язування гри пару задач лінійного проґрамування.

Таким чином розв’язання матричної гри зводиться до знаходження невід’ємних розв’язків системи лінійних нерівностей та рівнянь (тобто, може бути приведена до задачі лінійного програмування.

Теорема 5. Нехай є матрична гра з матрицею , ціною гри , оптимальними мішаними стратеґіями та гравців А та В відповідно. Тоді, якщо для деякого буде , то ; якщо для деякого буде , то .

Ця теорема ґрунтується безпосередньо на співвідношеннях між прямою та двоїстою задачами лінійного програмування, що відповідають грі.