4.3. Розв’язування задач змішаного та лінійного програмування за допомогою методу гілок та границь

Розглянемо лінійну задачу змішаного проґрамування. Нехай на певному кроці – змінна, на яку накладене обмеження цілочисельності, і яка має на даному кроці розв’язування неціле значення x*_r. Таким чином дійсне значення цієї змінної повинне на даному етапі знаходитися поза межами інтервалу [x*_r]<x*_r<[x*_r+1], тобто в цьому інтервалі оптимальних розв’язків немає. Тому значення x_r повинне задовільняти одну з двох нерівностей: x_r<=[x*_r] або x_r>=[x_r]+1. Введення цих двох взаємновиключаючих умов породжує дві не пов’язаних між собою задачі — тобто первісна задача розщеплюється на дві підзадачі. Таким чином здійснюється врахування необхідних умов цілочисельності – а саме виключаються частини многогранника припустимих розв’язків, які завідомо не мають точок з цілочисельними координатами.Після цього кожна з підзадач розв’язується як класична задача ЛП. Якщо отриманий оптимальний план є цілочисельним, то подальше розгалуження не проводиться і отримуємо оптимальний розв’язок підзадачі.

Ефективність методу підвищується шляхом введення границь – оцінок згори (для задачі максимізації) для підзадач. Це дозволяє при наявності біжучого розв’язку задачі відкинути ті підзадачі, для яких значення границі менше, ніж значення функції мети для біжучого розв’язку. Таким чином реалізується відтинання неперспективних підмножин розв’язків (підзадач) і зменшити об’єм роботи порівняно з методом повного перебору.

Приклад 2. Необхідно розв’язати наступну задачу.

.

Застосуємо до цієї задачі метод гілок та границь.Перебіг процесу розв’язування зображений нижче.

Структура та основні складові методу гілок та границь

Метод гілок та границь ґрунтується на ідеї розбиття первісної задачі на підзадачі та скорочення об’єму перебору за рахунок відсіювання підмножин неперспективних розв’язків первісної задачі, що реалізується шляхом обчислення оцінок значень функції мети (границь) або безпосереднім чином, або за допомогою розв’язування оціночних задач. З одного боку, чим ближче до оптимального значення функції мети для підзадачі значення границі, тим більше вірогідність того, що об’єм перебору буде меншим, а з іншого — чим складнішими є оціночні задачі, тим більшою буде працехлинність методу. Таким чином, в процесі синтезу алгоритму, що ґрунтується на методі гілок та границь, необхідно знайти оптимальний компроміс між точністю обчислення границь та складністю оціночних задач.

До основних елементів методу гілок та границь належать:

• дерево розгалужень;

• послаблена (релаксована) задача;

• границя;

• активні вузли дерева розгалужень;

• критерії відтинання вузлів;

• стратегія розгалуження.

Дерево розгалужень.

Процес розв’язування задачі за допомогою методу гілок та границь наочно представляється у вигляді динамічного дерева розгалужень з коренем , який відповідає первісній задачі, — множина вузлів дерева, що являють собою підзадачі, — множина дуг дерева розгалужень. В процесі розв’язування задачі деякі вузли відтинаються як неперспективні, замість них з’являються інші, тобто дерево розгалужень є динамічним. Розгалуження є розбиттям певної підзадачі на підзадачі наступного рівня, що пов’язані з задачею-предком дугами:

,

.

Послаблена (релаксована) задача.

Для кожного вузла дерева розв’язується послаблена (релаксована) задача — підзадача “занурюється” в ширший клас задач, для яких існують ефективні алґоритми їх розв’язування. Внаслідок розв’язання похідної послабленої задачі отримується “надоптимальний” розв’язок для основної підзадачі (верхня — у випадку максимізації границя значення критерію якості основної задачі).

Границя.

Границя є значенням критерію якості для оптимального розв’язку послабленої задачі. Границя має наступні властивості (вважаємо, що розв’язується задача максимізації):

• , де — значення границі, — значення критерію якості для оптимального розв’язку задачі ;

• , якщо — безпосередній нащадок ;

• , якщо — лист дерева розгалужень (лист відповідає побудові повного розв’язку первісної задачі ).

Активний вузол дерева розгалужень.

Вузли дерева розгалужень належать до однієї з наступних категорій:

• проміжні вузли, які вже розбиті на підзадачі (тобто вузли, що мають безпосередніх нащадків);

• листя дерева, в яких досягнутий розв’язок первісної задачі; якщо шукається один оптимальний розв’язок первісної задачі, то в дереві є один лист, що відповідає біжучому найкращому розв’язку, в іншому випадку кількість листя дерева може бути більшою;

• активні вузли дерева, які можуть бути піддані декомпозиції (розбиттю на підзадачі).

Вузол належить до множини активних, якщо виконуються наступні умови:

• не визначає повного припустимого розв’язку первісної задачі ;

• в даний момент (на біжучому етапі розв’язування задачі) не може бути встановлена справедливість умови , де — множина оптимальних розв’язків , — відповідно ;

• вузол не розбивався на підзадачі.

Критерії відтинання вузлів.

Для забезпечення ефективності методу гілок та границь необхідно відтинати якомога більш вузлів, якнайближчих до кореня. Це дозволяє відразу виключити з розгляду значні підмножини розв’язків та зменшити об’єм перебору. Для відтинання неперспективних вузлів використовується істинність умови . Ця умова завжди виконується, якщо виконується хоча б одна з наступних умов:

• перетин множини припустимих розв’язків для первісної задачі та підзадачі — пуста множина: ;

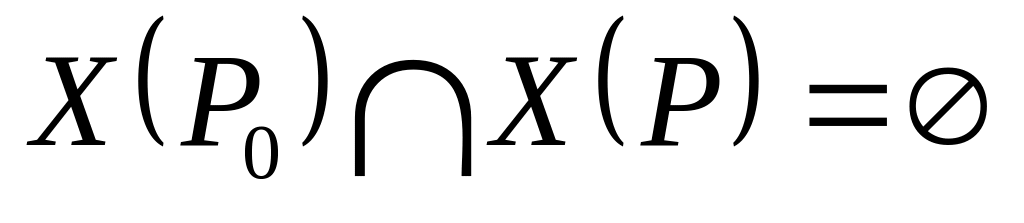• виконується умова відтинання вузла , де — значення критерію для найкращого біжучого (повного) розв’язку задачі;

• існує вузол , що не є предком , який домінує над ним — тобто встановлено, що , де — оптимальний розв’язок задачі , а — відповідно ; для встановлення цього факту зовсім не обов’язково знати відповідні значення;

• окрім того, відтинається вузол, який піддавався декомпозиції і у якого відтяті всі безпосередні нащадки.

Якщо для деякого вузла встановлено, що , то далі не розбивається, тому що знайдений один з повних розв’язків задачі. Коли ж , то найкращим біжучим розв’язком стає знайдений, , а вузол, що відповідав попередньому, відтинається.

Стратегія розгалуження.

Стратегія розгалуження визначає спосіб побудови динамічного дерева розгалужень та вибору наступного вузла з множини активних для декомпозиції. Структуру стратегії розгалуження представимо у вигляді двох відображень: та , де — множина числових значень. За допомогою відображення виділяється множина вузлів — кандидатів для декомпозиції, а за допомогою — вибір одного з них за допомогою кількісного критерію . Розглянемо наступні стратегії розгалуження: за найкращим значенням границі; вглиб дерева розгалужень; вшир дерева розгалужень; розгалуження пагонами.

В стратегії розгалуження за найкращим значенням границі на кожному кроці з числа активних обирається вузол з найбільшим (задача на пошук максимуму) значенням границі.

В стратегії розгалуження за найкращим значенням границі на кожному кроці з числа активних обирається вузол з найбільшим (задача на пошук максимуму) значенням границі, , .

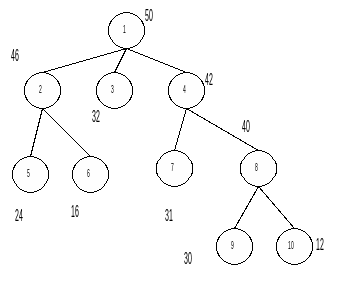
В прикладі біля вузлів проставлені значення границь. Номери вузлів відображають порядок породження нащадків згідно до стратегії розгалуження за кращим значенням границі. В багатьох випадках ця стратегія приводить до найкращого розв’язку за найкоротший час, але внаслідок тенденції до росту дерева вшир необхідні значні ресурси оперативної пам’яті для ефективної роботи відповідних алгоритмів. Крім того, необхідний досить значний час для знаходження першого біжучого найкращого розв’язку, тому в системах реального часу застосовувати її не варто.

В стратегії розгалуження вглиб дерева розгалужень на кожному кроці визначаються вузли, які знаходяться найдалі від кореня (віддаль від кореня дерева вимірюється як число ребер, що зв’язують вузол з коренем), і серед них обирається вузол з найбільшим значенням границі,

, .

Після того, як досягнутий розв’язок, відбувається повернення на рівень догори, і процедура повторюється.

Ця стратегія дозволяє за найкоротший час отримати найкращий біжучий розв’язок, але витрачає багато часу на його покращення внаслідок пошуку на сусідніх рівнях та гілках дерева розгалужень.

В стратегії розгалуження вшир дерева розгалужень на кожному кроці визначається множина вузлів, що розташовані найближче до кореня, і серед них здійснюється вибір вузла з найбільшим значенням границі:

, .

Ця стратегія приводить до переважного росту дерева розгалужень вшир і на практиці не застосовується.

Стратеґія розгалуження пагонами є комбінацією двох найпоширеніших стратегій — розгалуження за найкращим значенням границі та вглиб дерева. Ця стратегія спрямована на синтез позитивних особливостей вищенаведених стратегій — по-перше, якомога швидше досягнути повного розв’язку первісної задачі, і, по-друге, витрачати на пошук наступного біжучого оптимального розв’язку, що достатньо віддалений від біжучого, якомога менше часу. Згідно до цієї стратегії декомпозиція підзадач відбувається за стратегією вглиб дерева розгалужень до моменту, поки не буде досягнутий повний розв’язок. Після цього вибір наступного вузла для розгалуження відбувається згідно до стратегії розгалуження за найкращим значенням границі, і знову застосовується стратеґія розгалуження вглиб дерева.

Слід зазначити, що переваги чи недоліки тієї чи іншої стратеґії не є абсолютними, і в значній мірі залежать від особливостей конкретних типів задач.