3. Переходные процессы в последовательной rlc-цепи.

Рассмотрим два случая переходных процессов в последовательной RLC-цепи:

• последовательная RLC-цепь подключается к источнику постоянной Э.Д.С. Е;

• предварительно заряженный конденсатор разряжается на RLC цепь.

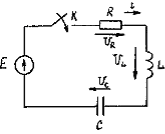
1. При подключении последовательной RLC-цепи к источнику постоянной Э.Д.С. Е (рис. 6.3.а) уравнение электрического равновесия цепи по второму закону Кирхгофа имеет вид:

U_L+U_R+U_C=E (6.10)

с учетом соотношений

U_R = R•i=R•C•(dU_C/dt);

U_L=L•(di/dt)=L•C•(d²U_C/dt²)

уравнение (6.10) можно записать в виде:

L•C•(d²U_C/dt²) + R•C•(dU_C/dt) + U_C = E (6.11)

а	б	в
Рис. 6.3

Решение неоднородного дифференциального уравнения (6.11) опреде­ляется характеристическим уравнением: LCp²+RCp+1=0,

которое имеет корни

(6.12)

где

δ=R/2L - коэффициент затухания,

- резонансная частота.

В зависимости от соотношения δ² и ω² возможны три основных вида переходных процессов:

а) δ² > ω² или Корни характеристического уравнения – отрицательные вещественные. Переходный процесс имеет апериодический характер (рис. 6.3.б).

б) δ² < ω² или Корни характеристического уравнения – комплексные и сопряженные. Характер переходного процесса - колебательный и затухающий (рис. 6.3.в)

в) δ² = ω² или Корни характеристического уравнения вещественные и равные p₁=p₂=-R/2L. Характер переходного процесса - апериодический и затухающий (критический случай). Время переходного процесса минимальное.

Для первых двух случаев решение уравнения имеет вид:

(6.13)

где

V=U_C(0) - напряжение на конденсаторе в момент коммутации.

Для случая δ² < ω² уравнение (6.13) приводится к виду:

, (6.14)

где

- частота затухающих колебаний.

Из уравнения (6.14) следует, что переходный процесс U_c(t) имеет ха­рактер колебаний с угловой частотой ω и периодом Т=2π/ω , которые затухают с постоянной времени τ=2L/R=1/δ.

Для определения величины постоянной времени τ можно использовать огибающую колебательной кривой U_c(t), имеющую форму экспоненты:

exp(-δt)=exp(-t/τ).

Для третьего случая δ=ω₀ решение уравнения (6.11) имеет вид:

. (6.15)

Особенность этого режима состоит в том, что при уменьшении R ниже значения переходной процесс становится колебательным.

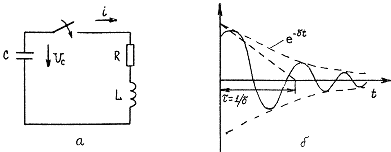
Рис. 6 4

2. При разряде конденсатора на RL-цепь (рис 6.4.а) возможны все три режима, рассмотренные выше и определяемые соотношением величин δ и ω₀. Переходные процессы в этих режимах описываются уравнениями (6.13), (6.14), (6.15) при Е=0. Например, для случая δ<ω₀ уравнение (6.14) при колебательном разряде конденсатора имеет вид:

(6.16)

Кривая переходного процесса U_c(t) приведена на (рис. 6. 4.б). Огибаю­щей кривой U_c(t) является функция exp(-δt)=exp(-t/τ), которая может быть исполь­зована для определения постоянной времени τ и коэффициента затухания δ=1/τ.

Оборудование для проведения работы и объекты исследования.

Работа проводится на универсальном лабораторном стенде ЭВ-4. Используется панель № 7, электрическая схема которой приведена на рис 6. 5

На панели № 7 установлен электронный коммутатор ЭК для форми­рования последовательности прямоугольных импульсов напряжения с по­стоянной амплитудой, длительностью и паузой, а также резисторы, кон­денсаторы и катушка индуктивности с указанием их параметров (сопротивления, емкости, индуктивности)

Используется также панель № 8, где установлены электронный осцил­лограф С1-118А и цифровой вольтметр (см. приложения 2-4).

Для питания электронного коммутатора ЭК стабилизированным на­пряжением +12В используется панель источников питания. Подключение осциллографа и вольтамперметра производится специальными соедини­тельными проводами, входящими в комплект стенда ЭВ-4.

Объектами исследования являются цепи RC, RL, RLC, расположенные на панели № 7

Рис. 6.5

Порядок выполнения работы и указания по технике безопасности

1. Построить графики переходных процессов U_c(t), i(t) при зарядке конденсатора для следующих параметров последовательной RC-цепи:

E= 9 В, С=0,01мкФ, R=20; 60; 100 кОм.

Для построения кривых U_c(t), i(t) использовать 3 характерных точки, для чего рассчитать постоянную времени τ и время переходного процесса Т_n. Результаты расчетов занести в таблицу 6.1

Таблица 6.1

R, кОм	τ, мкс		Тn, мкс
	Расчет	Измерение	Расчет	Измерение
20
60
100

2. Используя формулы (6.5), (6.6), построить графики переходных про­цессов U_c(f), i(t) при разряде конденсатора для следующих параметров RC-цепи Uc(0)=9 В; С=0,01 мкФ; R=20; 60; 100 кОм.

3. Для последовательной RL-цепи рассчитать постоянную времени τ и длительность переходного процесса Т_n,на основании которых построить приближенные кривые U_L(t), U_R(t) при следующих параметрах цепи: Е= 9 В, L=66 мГн, R=0,11; 5,11; 10,11 кОм. Результаты расчетов зане­сти в таблицу 6.2.

Таблица 6. 2

R, кОм	τ, мкс		Тn, мкс
	Расчет	Измерение	Расчет	Измерение
0,11
5,11
10,11

4. Рассчитать сопротивление R_Σ для последовательной RLC-цепи с С=0,01 мкФ, L=66 мГн , при котором переходный процесс имеет аперио­дический, критический и колебательный характер. Для колебательного процесса рассчитать частоту затухающих колебаний ω, собственную частоту колебаний ω₀ и коэффициент затухания δ Результаты расчетов за­нести в таблицу 6.3

Таблица 6.3

Режим	RΣ, Ом	ω, с-1		ω, с-1		δ, с-1
		Расчет	Измерение	Расчет	Измерение	Расчет	Измерение
Колебательный
Критический
Апериодический

5. Подключить экспериментальную установку для исследования пере­ходных процессов (панель № 7) к стабилизированному источнику постоянного напряжения U=12 В и ключом К1 включить электронный коммута­тор (рис 6.5). Включить напряжение питания осциллографа С1-72 нажати­ем кнопки "сеть" на передней панели прибора, осуществить его прогрев в течение 5 минут.

6. Переключателем К2 подключить к выходу ЭК левую часть схемы, содержащую резистор 1 кОм и последовательную RC-цепь, состоящую из переменного резистора 0÷100 кОм и конденсатора 0,01 мкФ.

7. Подать на вход “y” осциллографа напряжение с резистора 1 кОм, используя для этого соединительный кабель со штекером, входящий в комплект осциллографа.

8. Установить на экране осциллографа изображение полутора-двух периодов напряжения. По полученной временной зависимости U(t) на экра­не осциллографа определить:

• амплитуду напряжения импульса U_M;

• длительность импульса T_U;

• длительность паузы T_ПЗ;

• частоту коммутации f электронного коммутатора.

Результаты занести в таблицу 6. 4.

Таблица 6. 4

UM, В	TU, мкс	TПЗ, мкс	f, Гц

9. Провести исследование переходных процессов в последовательной электрической RC-цепи с резистором и конденсатором:

• переключить вход осциллографа с резистора R=1 кОм на конденса­тор С=0,01 мкФ. При трех различных сопротивлениях переменного резистора (R=20; 60; 100 кОм) зарисовать осциллограммы напряжений U_С(t) на конденсаторе и U_R(t) на резисторе при переходных процессах. Значения переменного резистора установить при помощи прибора В7-38, предварительно отключив напряжение питания + 12В:

• для каждой осциллограммы установить масштабы по осям времени и напряжения.

10. Исследовать переходные процессы в последовательной RL-цепи с резистором и катушкой индуктивности;

• при помощи переключателей K2 и КЗ включить под прямоугольное напряжение электронного коммутатора последовательную электрическую цепь, состоящую из переменного резистора 10 кОм, постоянного резистора 100 Ом и катушки индуктивности с параметрами L=66 мГн, R_К=12 Ом. Конденсатор С=0,01 мкФ должен быть отключен переключателем К3;

• снять осциллограмму подаваемого на исследуемую цепь прямоугольного напряжения и сравнить его амплитуду U_M, длительность импульса Т_U паузы Т_ПЗ и частоту импульсов f с результатами п. 8.

• снять с экрана осциллографа осциллограммы напряжений на участке цепи, состоящей из катушки индуктивности, резистора R=10 кОм и посто­янного резистора 100 Ом, при трех значениях сопротивления переменного резистора R = 100 Ом; 5кОм и 10 кОм. Значения сопротивления перемен­ного резистора устанавливать в соответствии с рекомендациями п. 9.

11. Исследовать процессы в последовательной RLC-цепи, состоящей из конденсатора и катушки индуктивности:

• переключателем КЗ переключить конденсатор С=0,01 мкФ к RL-цепи, которая исследовалась в п.10. Провести три опыта при значениях суммарного сопротивления резисторов

;

;

;

Измерения сопротивления резистора произвести в соответствии с п. 9.

• при выполнении опытов зарисовать осциллограммы напряжений на конденсаторе/

Обработка результатов

1. По осциллограммам U_С(t) опыта п. 9 определить постоянные вре­мени исследуемых RC-цепей при зарядке и разрядке конденсатора, запи­сать их численные значения в таблицу 6.1. Определить относительную по­грешность измерения постоянных времени по формуле:

2. По осциллограммам U_L(t) опыта п. 10 определить постоянные вре­мени исследуемых RL-цепей при переходных процессах и записать их численные значения в табл. 6.2. Определить погрешность измерения по­стоянных времени по формуле, приведенной выше.

3. По осциллограмме U_С(t) (п. 11), соответствующей колебательному переходному процессу, определить частоту собственных затухающих коле­баний и коэффициент затухания исследуемой RLC-цепи Результаты зане­сти в табл. 6.3. Сравнить экспериментальные и расчетные значения этих величин.

Контрольные вопросы

1. Для какой цели используются два закона коммутации электрических цепей, содержащих конденсаторы и катушки индуктивности?

2. Что такое постоянная времени электрической цепи?

3. В течение какого промежутка времени заканчивается переходный процесс в электрической цепи?

4. Как определить постоянную времени по экспериментальным зависимостям тока и напряжения при переходном процессе?

5. Как рассчитать постоянную времени неразветвленных RC- и RI-цепей?

6. Как определить емкость конденсатора или сопротивление резистора по кривой зарядки или разрядки конденсатора через этот резистор, если известен один из этих параметров?

7. Как изменяется характер переходного процесса при увеличении со­противления R в последовательной RLC-цепи?

8. Что характерно для критического случая апериодического переходного процесса?