1. Переходные процессы в rc-цепи.

а	б
в	г
Рис. 6.1

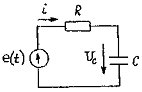
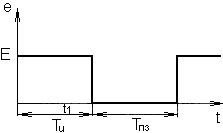
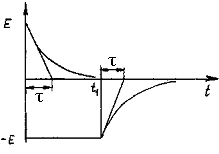
Рассмотрим последовательную RC-цепь (рис. 6.1.а), к которой под­ключен источник Э Д С e(t), формирующий импульс напряжения с амплитудой Е и длительностью Т_и (рис.6.1.б)

Заряд конденсатора

В интервале времени 0<t<t₁ конденсатор С заряжается. По закону Кирхгофа для этой цепи имеем Ri + U_c=E Так как

i= С dU_c /dt,

то

RС (dU_c/dt) + U_C =E (6.1)

при начальном условии:

U_c(0) = О Решение уравнения (6.1) имеет вид:

U_c(t)=E(l-e^-t/τ), (6.2)

где

τ=RC - постоянная времени

Тогда:

i=(E/R) e^-t/τ _(6.3)

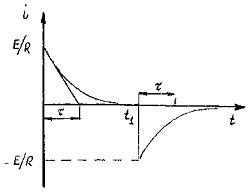
Кривые переходных U_c(t), i(t) приведены на рис. 6.1. в, г.

Время, в течение которого напряжение U_c(t) достигает величины 0,95 E ориентировочно составляет Т_п = (3-4)τ .

За время Т_п ток заряда конденсатора i(t) уменьшается до величины 0,05 E/R. Касательные, проведенные к кривым U_c(t) или i(t) в момент вре­мени t=0, отсекают на прямых U_C(∞)=E и I(∞)= 0 отрезки, равные интерва­лу времени τ, что позволяет по экспериментальным кривым U_c(t), i(t) оп­ределить параметры RC-цепи: R=E/i(0), C=τ/R.

Если параметры цепи Е, R, С заданы, то приближенные кривые U_с(t), i(t) при U_c(0)=0 можно построить по трем характерным точкам для сле­дующих моментов времени:

при t=0 имеем U_c(0)=0, I(0)=E/R;

при t=( τ ) имеем U_c(t)=0,63E, i(τ)=0,37E/R;

при t=T_n имеем U_C(T_n)=E, i(T_n)=0

Разряд конденсатора

В момент времени t=t₁ начинается разряд конденсатора С через рези­стор R и источник Э. Д. С, внутреннее сопротивление которого равно нулю. По второму закону Кирхгофа для этой цепи в интервале времени t₁<t<∞ имеем:

Ri+U_c=0 или RC(dU_c/dt)+U_c=0 ' (6.4)

при начальном условии

U_c(0)=E

Если принять, что коммутация проходит в момент времени t=0 (начало координат смещается в точку t₁), то решение диф. уравнения (6.4) принимает вид:

U_с(t)=Е e^-t/τ (6.5)

Тогда

i=(t)=-(E/R)e^{-t/τ (6.6)}

где:

τ=RC Отрицательный знак в выражении (6.6) указывает на противоположное направление тока по сравнению с направлением тока при заряде конден­сатора (рис. 6 1. г)

2. Переходные процессы в RL-цепи

а	б
в	г
Рис. 6.2

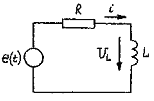
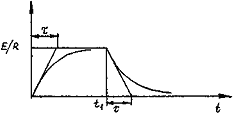
Рассмотрим последовательную RL-цепь (рис.6.2.а) с подключенным источником ЭДС e(t), формирующим импульс напряжения с амплитудой Е и длительностью Т_и (рис.6.2.б)

В интервале времени (0<t<t₁) уравнение электрического равновесия RL-цепи имеет вид

U_L+R i=E Так как

U_L=L (di/dt), то получим

L (di/dt)+R i=E (6.7)

Решение уравнения (6.7) при начальном условии i_L(0)=0 имеет вид

i(t)=E/R (1-e^-t/τ ), (6.8)

где

τ=L/R - постоянная времени

Тогда напряжение на индуктивности

U_L(t)=E e^-t/τ (6.9)

Кривые переходного процесса i(t) и U_L(t) приведены на рис 6.2 в,г

Время переходного процесса, за которое ток i(t) практически достигает установившегося значения E/R, а напряжение U_L(t) спадает до нуля, составляет Т_и=(3…4)τ .

Касательные, проведенное к кривым i(t) или U_L(t) в момент времени t=0, отсекают на прямых i(∞)=E/R и Ul(∞)=0 отрезки, равные интервалу времени τ, что позволяет по экспериментальным кривым i(t) и U_L(t) опре­делить параметры R и L

R=E/i(∞), L=R τ

Если параметры цепи Е, R, L заданы, то приближенные кривые i(t), U_L(t) при начальном условии i(0)=0 можно построить по трем характерным точкам для следующих моментов времени

при t=0 имеем i(0)=0, U_L(0)=E,

при t= τ имеем i(t)=0,63 E/R, U_L(τ )=0,37,

при t=T_u имеем i(Tн)-=E/R, U_L(Tн)=0