6. Наиболее часто встречающиеся законы распределения
Нормальное распределение:
-
функция плотности;
-
функция нормального распределения.
Запись
означает, что случайная величина
имеет нормальное распределение с
параметрами
- математическое ожидание и
- среднеквадратическое отклонение. В
случае выборок из нормальной совокупности
(нормальных выборок) все выборочные
значения являются нормальными случайными
величинами
Распределение «хи-квадрат»:
Пусть
случайные величина, нормально
распределенные, причем, матожидание
равно 0, а стандартное отклонение равно
1. Тогда сумма квадратов этих величин
имеет
распределение
(хи-квадрат) с k=n
степенями свободы. Если же величины
связаны одним линейным соотношением,
например,
,
то число степеней свободы равно k=n-1.
Доказано, что при
распределение медленно приближается
к нормальному. Запись
означает, что случайная величина
имеет
распределение
с
степенями свободы.
Распределение Стъюдента:
Пусть
-
две независимые случайные величины.
Тогда величина
имеет t-распределение Стъюдента (псевдоним английского математика Госсета), с k степенями свободы. Доказано, что с возрастанием числа степеней свободы распределение Стъюдента быстро приближается к нормальному.
Запись
означает, что случайная величина
имеет
распределение
Стъюдента с
степенями свободы.
F-распределение Фишера-Снедекора:
Пусть
-
две независимые случайные величины.
Тогда величина
имеет
F-распределение
Фишера-Снедекора со степенями свободы
.
Запись
означает, что случайная величина
имеет
-распределение
Фишера-Снедекора с
степенями свободы.
7. Примеры использования описательной статистики в экспериментальных исследованиях
Пример 1. В комплексном исследовании личности в учебной группе из 50 человек были получены оценки нейротизма по Айзенку. Исследовать полученные результаты и сделать выводы. Оценки могут принимать только целочисленные значения, следовательно признак является дискретным.
15, 20, 15, 22, 9, 12, 15, 16, 15, 16, 16, 17, 20, 22, 7, 22, 12, 12, 15, 12, 15, 7, 10, 17, 12, 9, 12, 9, 9, 3, 15, 15, 7, 15, 7, 16, 12, 20, 12, 9, 12, 15, 10, 16, 20, 9, 15, 10, 17, .15
Статистическое распределение будет иметь вид:
|
3 |
7 |
9 |
10 |
12 |
15 |
16 |
17 |
20 |
22 |
|
1 |
4 |
6 |
3 |
9 |
12 |
5 |
3 |
4 |
3 |
N=50, k=10.
Вычислим оценки параметров распределения:
=
= (12+15)/2 = 14,5; = 15;
= (3-13,7)2
1
+(7-13,7)2
4
+(9-13,7)2
6
+(10-13,7)2
3
+(12-13,7)2
9
+
+(15-13,7)2 12+(16-13,7)2 5+(17-13,7)2 3+(20-13,7)2 4+(22-13,7)2 3 =
= 938,5/49 = 19,1;
σ = 4,37; V = (4.37/13.7) 100% = 31,89%
=( (3-13,7)3 1 +(7-13,7)3 4 +(9-13,7)3 6 +(10-13,7)3 3+(12-13,7)3 9 +
+(15-13,7)3 12+(16-13,7)3 5+(17-13,7)3 3+(20-13,7)3 4+(22-13,7)3 3)/4172,6= = 1,47;
= ((3-13,7)4 1 +(7-13,7)4 4 +(9-13,7)4 6 +(10-13,7)4 3 +(12-13,7)4 9 +
+
(15-13,7)4
12+(16-13,7)4
5+(17-13,7)4
3+(20-13,7)4
4+(22-13,7)4
3)/18240
= 3,9
Рис.3.
-
Выборочное среднее
13,7
Медиана
14,5
Мода
15
Выборочная дисперсия
19,1
Выборочное сред.квадр.отклонение
4,37
Коэффициент вариации
31,9
Асимметрия
1,47
Эксцесс
3,9
Пример 2. В опыте по изучению амплитудно-частотной характеристики руки человека при слежении за движущимся объектом получены значения амплитуды для одного испытуемого
65 |
62 |
63 |
65 |
73 |
58 |
68 |
55 |
72 |
52 |
55 |
70 |
62 |
57 |
69 |
55 |
60 |
68 |
61 |
65 |
71 |
60 |
71 |
58 |
67 |
72 |
46 |
58 |
63 |
64 |
58 |
66 |
63 |
63 |
64 |
52 |
55 |
59 |
60 |
62 |
65 |
66 |
72 |
56 |
56 |
64 |
64 |
82 |
60 |
62 |
70 |
55 |
64 |
65 |
70 |
54 |
75 |
67 |
70 |
60 |
61 |
60 |
73 |
74 |
51 |
60 |
63 |
64 |
65 |
63 |
52 |
58 |
80 |
68 |
63 |
59 |
69 |
59 |
59 |
|
65 |
60 |
62 |
71 |
65 |
60 |
54 |
|
62 |
60 |
62 |
63 |
68 |
58 |
64 |
|
58 |
62 |
46 |
62 |
57 |
62 |
49 |
|
Построить статистическое распределение, сделать статистический анализ на основе описательной статистики.
n=100, xmax = 82, xmin = 46, R = 36.
Число интервалов k = k=1+3,332lg(n) = 8, длина интервала h=4,5.
Статистическое распределение имеет вид:
Интер- вал |
[46-50,5) |
[50,5-55) |
[55-59,5) |
[59,5-64) |
[64-68,5) |
[68,5-73) |
[73-77,5) |
[77,5-82) |
Серед интерв |
48,25 |
52,25 |
57,25 |
61,75 |
66,25 |
70,75 |
75,25 |
79,75 |
Частота |
3 |
11 |
15 |
37 |
16 |
14 |
2 |
2 |
=
;
= 62; = 60; = 43,6; σ = 6,6;
V = (6,6/62,5) 100% = 11% ; = 0,14; = 0,6.
Замечание 1. Для построения вариационного ряда необходимо:
- На отдельном листе рабочей книги EXCEL создать таблицу исходных данных.
- Подсчитать максимальное и минимальное значение вариант, используя функции MAX и MIN. Для этого зайдите в f*, Статистические, MAX или MIN. Инструкцию использования этих функций найдите в справке “ ? ”.
- Рассчитать длину частичного интервала по формуле
h = (Xmax - Xmin)/k.
- Подсчитать нижние и верхние границы частичных.
- Подсчитать значение середины интервалов Xс = (Xi + Xi+1)/2.
- Подсчитать частоты, используя мастер функций: f*, Статистические, Частота. Смотрите справку по использованию последней функции. Например,
сначала надо пометить массив, в который будут записаны частоты;
далее вызвать мастер функций и в массив_данных записываете адрес исходного массива;
в двоичный_массив записываете адрес массива карманов, в данном случае можно взять адрес массива верхних границ частичных интервалов;
затем поместить курсор на конец командной строки и нажать Ctrl Shift Enter именно в такой последовательности. В результате этого в столбце частот появятся значения частот.
Замечание 2.
Для построения гистограммы необходимо:
- Войти в пакет программ «Анализ»:
Сервис
Анализ
Гистограмма
- Ввести необходимую информацию:
адрес массива исходных данных;
адрес массива карманов (он совпадает с адресом массива верхних границ);
адрес метки (верхний левый угол новой области расположения гистограммы).
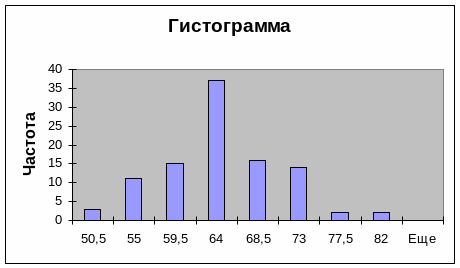Рис.4.
Выборочное среднее |
62,5 |
Медиана |
62 |
Мода |
60 |
Выборочная дисперсия |
43,6 |
Выборочное сред.квадр.отклонение |
6,6 |
Коэффициент вариации |
11 |
Асимметрия |
0,14 |
Эксцесс |
0,6 |
Пример 3. Изучаются библиографические характеристики случайно выбранных статей, опубликованных в журнале «Российская медицинская ассоциация» за 1995-2005 годы. Интересующий показатель – число авторов статьи. Доказано, что распределение числа авторов является нормальным. Подсчитано выборочное среднее 2,8 и исправленное среднеквадратическое отклонение 0,8. Определить доверительный интервал для математического ожидания числа авторов с надежностью 0,95.
Дано:
.Найдем
квантиль порядка γ
=
=
=2,005.
Найдем границы доверительного интервала:
,
.
Итак, с надежность 0,95 математическое ожидание числа авторов заключено в интервале (2,58; 3,01).