Транзитивная зависимость и третья нормальная форма. Примеры.
В отношении R присутствует транзитивная зависимость, если в нем имеются такие наборы атрибутов А, В, С, С В, В А что:
А В, В С; при этом В А
1) Условие В А необходимо, чтобы исключить тривиальную транзитивную зависимость типа следующей:
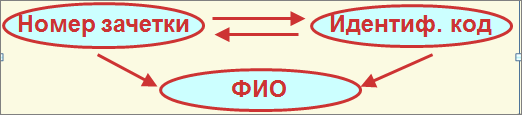
2) Условия С В, В А необходимы, чтобы исключить следующие тривиальные транзитивные зависимости:
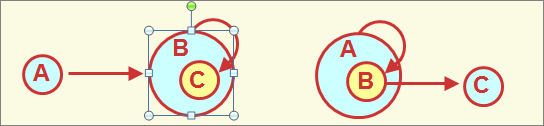
Аномалии вставки, удаления, замены при наличии транзитивной зависимости
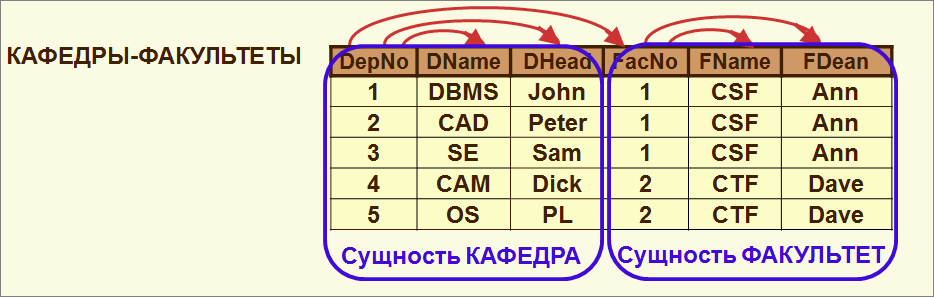
Наличие в отношении транзитивной зависимости свидетельствует, что отношение содержит информацию о более, чем одной сущности.
Как следствие, такое отношение влечет аномалии вставки, удаления, замены.
Третья нормальная форма (3NF)
Отношение находится в третьей нормальной форме, если оно находится во второй нормальной форме и не содержит транзитивных зависимостей непервичных атрибутов от возможных ключей.
Другими словами все непервичные атрибут должны функционально зависеть только от возможных ключей
Алгоритм приведения к 3NF. Пусть задано отношение R со множеством атрибутов M. Если в R имеется транзитивная функциональная зависимость R.A R.B и R.В R.С неключевого атрибута С от возможного ключа А, то отношение R разбивается на следующие два отношения: R[В, С] и R[M - С]. Если результирующие отношения все еще не находятся в третьей нормальной форме, то к ним опять применяется этот алгоритм.
Пример приведения в 3NF
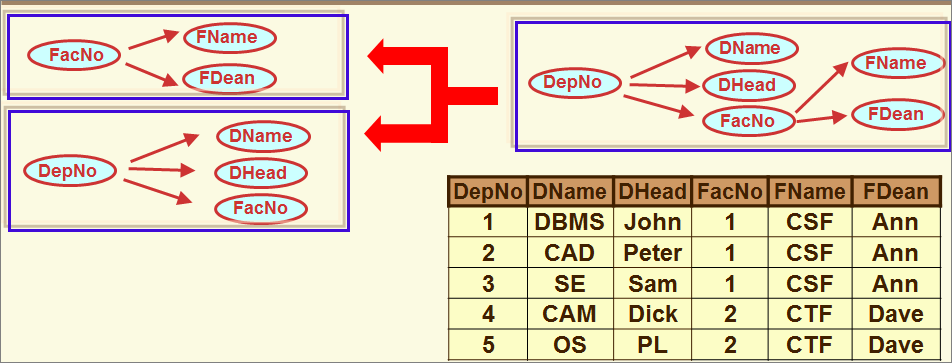
Пример приведения в 3NF – итоги
Исходное отношение содержит информацию о двух сущностях, результирующие – каждое по одной сущности.
Результирующие отношения не содержат аномалий вставки, удаления, замены.
Исходное отношение можно восстановить из результирующих с помощью операции естественного соединения.
При таком разбиении не теряются функциональные зависимости (то есть зависимости исходного и результирующих отношений эквивалентны)
Усиленная третья нормальная форма и нормальная форма Бойса-Кодда. Примеры
3NF требует отсутствия транзитивной зависимости именно непервичных атрибутов, а не всех атрибутов отношения. Усиленная 3NF требует отсутствия транзитивной зависимости для ВСЕХ атрибутов отношения.
Это отношение находится в 3NF, но содержит информацию о двух сущностях и поэтому обладает аномалиями
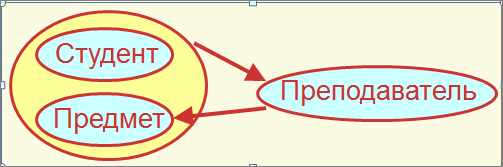
Отношение находится в усиленной третьей нормальной форме, если оно находится во второй нормальной форме и не содержит транзитивных зависимостей ВСЕХ атрибутов от возможных ключей
Приведение в S3NF
Алгоритм приведения к S3NF такой же, как в 3NF
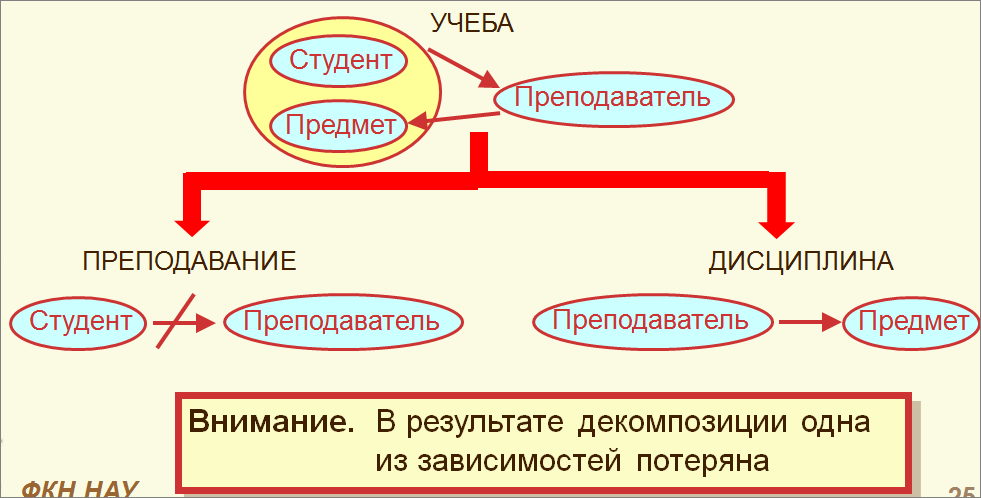
Нормальная форма Бойса-Кодда (BCNF)
Отношение R находится в нормальной форме Бойса-Кодда, если любой детерминант является суперключом
Утверждение. Усиленная третья нормальная форма и нормальная форма Бойса-Кодда эквивалентны
Многозначная зависимость. Определение. Примеры.
Пусть задано отношение R с атрибутами (или наборами атрибутов) А, В, С. Говорят, что существует многозначная зависимость В от А (или А многозначно определяет В), и это обозначается как А ®® В, если при заданных значениях атрибутов из А существует множество связанных значений атрибутов из В и это множество В-значений не зависит от значений атрибутов из С .
Пример: В отношении УЧЕБА имеются следующие MVD:
Предмет ®® Преподаватель Предмет ®® Учебник
Пусть задано отношение R(A,B). MVD А ®® Æ и А ®® В называются тривиальными так как они присутствуют во любых отношениях .
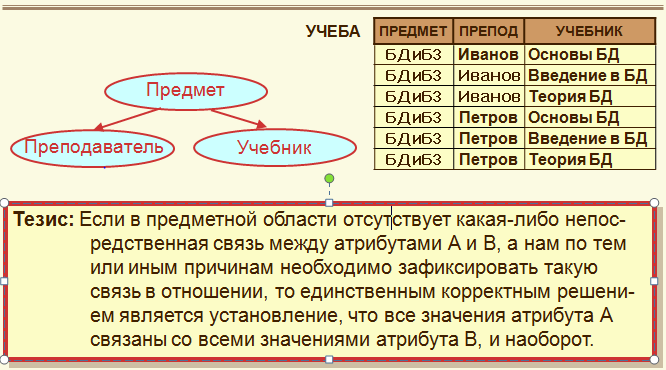
Свойства многозначных зависимостей. Примеры.
Аксиомы MVD
Пусть R состоит из атрибутов (или набора атрибутов) А, В, С.
MVD обладают следующими аксиомами:
1) Аксиома дополнения
Если А ®® В, то А ®® С
2) Аксиома пополнения
Если А ®® В и V Í W, то (А, W) ®® (В, V)
3) Аксиома транзитивности
Если А ®® В и В ®® С, то А ®® С – В
Существуют следующие две аксиомы, которые связывают многозначные и функциональные зависимости.
Аксиома репликации
Если А ® В, то А ®® В
2) Аксиома соединения
Если А ®® В и Z Í B, и для некоторого W, непересекающегося с B имеем W ® Z, то A ® Z
Дополнительные свойства MVD
1) Объединение
Если А ®® В и А ®® С, то А ®® (В, С)
2) Псевдотранзитивность
Если А ®® В и (W, В) ®® Z ,
то (W, А) ®® Z – (W, В)
3) Смешанная псевдотранзитивность
Если А ®® В и (А,В) ®® С, то А ®® (С - В)
4) Пересечение и разность
Если А ®® В и А ®® С, то А ®® В Ç С, А ®® В – С, А ®® С – В