Лекция № 10. Общие понятия о модуляции.
Модуляция – это процесс изменения одного или нескольких параметров несущей в соответствии с изменением параметров сигнала, воздействующего на нее (модулирующего сигнала).
Параметры несущей, изменяющиеся во времени под воздействием модулирующего сигнала, называются информационными, так как в них заложена передаваемая информация. Физический процесс управления параметрами несущей и является модуляцией. Устройство, при помощи которого получают модулированные сигналы, называется модулятором.
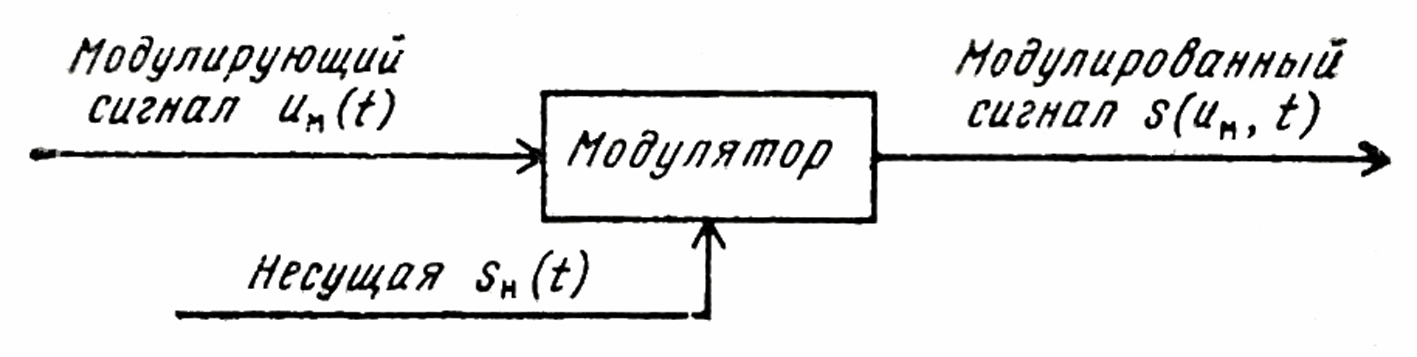
Модулятор.
Модулятор
должен иметь два входа: один для
модулирующего (информационного) сигнала,
другой – для несущей. Модулированный
(высокочастотный) сигнал на выходе
модулятора зависит от времени и от
модулирующего сигнала
,
поэтому и обозначается как функция двух
аргументов
.
Модулированные сигналы различаются по виду несущей и по модулируемым параметрам. В качестве несущей чаще всего используются гармонические колебания, периодическая последовательность импульсов, реже – колебания специальной формы, узкополосный случайный процесс.
Гармоническая
несущая
характеризуется тремя свободными
параметрами: амплитудой
,
частотой
и фазой
.
Все они могут быть информационными. В
результате изменения одного из этих
параметров при постоянстве других,
получим три основных вида модуляции:
амплитудную модуляцию (АМ);
частотную модуляцию (ЧМ);
фазовую модуляцию (ФМ).
Модулированный сигнал при гармонической несущей в общем случае можно представить в виде
,
где
– огибающая сигнала;
– полная фаза.
За
интервал времени, в течении которого
полная фаза
изменится на
,
огибающая не успеет сильно измениться
и ее можно считать медленно меняющейся.
Главная особенность любой модуляции – это преобразование спектра модулирующего сигнала. В общем случае происходит расширение спектра, а при гармонической несущей – перенос спектра в область около частоты несущей. Именно это обстоятельство и привело к использованию только модулированных сигналов в радиосвязи и многоканальной связи.
Практически в настоящее время в системах связи используется более пятидесяти видов модуляции и число их продолжает расти. Такое большое количество различных видов модуляции связано с тем, что каждый из них имеет свою помехоустойчивость. Поэтому, прежде всего надо учитывать способность данного вида модуляции обеспечить заданное качество передачи сообщений по линии связи при наличии помех.
Лекция № 11. Амплитудная модуляция (ам) гармонической несущей.
Амплитудной
модуляцией (АМ) называется процесс
изменения амплитуды несущего колебания
под воздействием модулирующего сигнала
.
В результате амплитуда несущей получает
приращение
и становится равной
,
где
– амплитуда несущей;
– коэффициент пропорциональности,
выбираемый так, чтобы амплитуда
всегда была положительной. Частота и
фаза несущего гармонического колебания
при АМ остаются неизменными.
Н
а
рисунке показано, что в соответствии с
мгновенными значениями
амплитуда несущей
увеличивается до значения
получая приращение
,
то уменьшается до
,
получая приращение
.
При этом амплитуда
повторяет форму модулирующего сигнала
.
В АМ сигнале амплитуда
является огибающей высокочастотного
заполнения
,
которая на рисунке изображена штриховой
линией.
Коэффициент модуляции.
Для
математического описания АМ сигнала
вместо коэффициента пропорциональности
,
зависящего от конкретной схемы модулятора,
вводится коэффициент модуляции
,
который физически означает относительное
значение приращения. Здесь
– среднее арифметическое значение
приращения амплитуды. Поскольку среднее
значение амплитуды АМ сигнала во время
модуляции
,
то коэффициент модуляции численно равен
.
Коэффициент
модуляции – это отношение разности
между максимальным и минимальным
значениями амплитуд АМ сигнала к сумме
этих значений.
Часто коэффициент модуляции выражается
в процентах
.
Однако при всех расчетах АМ сигналов
обычно пользуются коэффициентом
модуляции
не в процентах, а в относительных
единицах.
Для
симметричного модулирующего сигнала
АМ сигнал также будет симметричным:
и
,
то есть
коэффициент
модуляции равен отношению максимального
приращения амплитуды к амплитуде
несущей.
Физически
характеризует собой глубину амплитудной
модуляции и может изменяться в пределах
.
Аналитическое выражение (математическая модель) любого АМ сигнала, с учетом коэффициента модуляции, будет выглядеть следующим образом:
.
Амплитудная модуляция гармоническим колебанием.
В
простейшем случае модулирующий сигнал
является гармоническим колебанием с
частотой
и начальной фазой
.
При этом аналитическое выражение
однотонального АМ сигнала будет выглядеть
следующим образом:
На рисунке показаны временные диаграммы однотонального АМ сигнала при различных значениях коэффициента модуляции .
Характерное искажение сигнала возникает при перемодуляции, когда форма огибающей перестает повторять форму модулирующего гармонического колебания.
В
однотональном АМ сигнале имеется три
гармонических спектральных составляющих
с частотами:
– несущей;
– верхней боковой;
– нижней боковой.
Спектральная
диаграмма однотонального АМ сигнала
симметрична относительно несущей
частоты
.
Амплитуды боковых колебаний одинаковы
и даже при
не превышают половины амплитуды несущего
колебания.
Амплитудная модуляция при сложном модулирующем сигнале.
Гармонические модулирующие сигналы и соответственно однотональный АМ сигнал на практике встречаются редко. В большинстве случаем модулирующие первичные сигналы являются сложными функциями времени.
Спектр
АМ сигнала при сложном модулирующем
сигнале
можно построить исходя из следующих
рассуждений. Любой сложный сигнал
можно представить в виде суммы конечной
(или бесконечной) гармонических
составляющих, воспользовавшись рядом
Фурье. Каждая гармоническая составляющая
сигнала
с частотой
вызовет в АМ сигнале две боковые
составляющие с частотами
.
Множество гармонических составляющих
в модулирующем сигнале
вызовет множество боковых составляющих
с частотами
.
Это показано на рисунке.
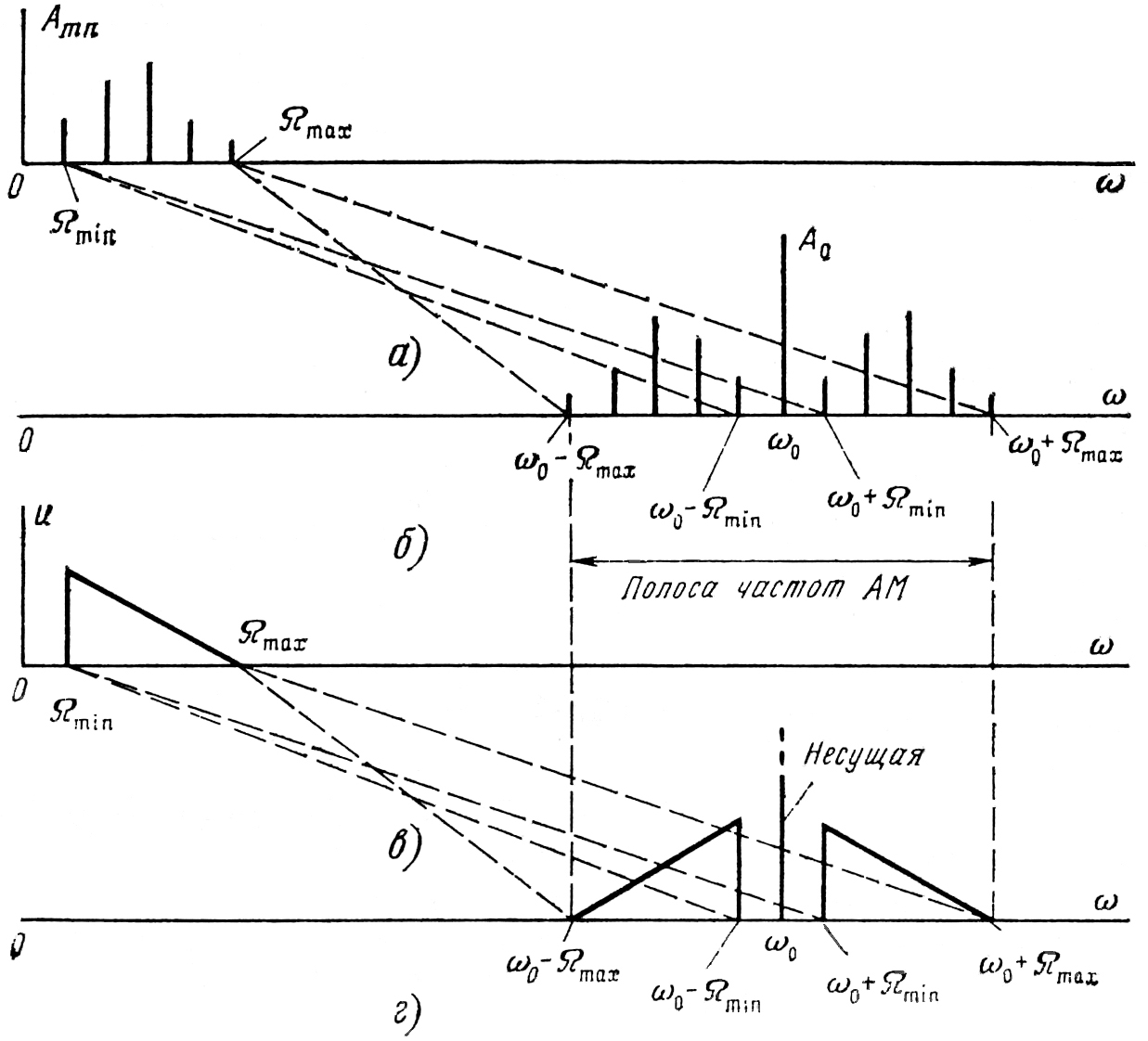
Спектральные диаграммы: а) – модулирующего многотонального сигнала; б) – АМ сигнала при многотональной модуляции; в) – модулирующего сигнала с непрерывным спектром; г) – АМ сигнала при модуляции сигнала непрерывным спектром.
В спектре сложномодулированного АМ сигнала, кроме несущего колебания с частотой , содержатся группы верхних и нижних боковых колебаний, которые образуют верхнюю боковую и нижнюю боковую полосу АМ сигнала. При этом верхняя боковая полоса частот полностью повторяет спектральную диаграмму сигнала , сдвинутую в область высоких частот на величину . Нижняя боковая полоса частот также повторяет спектральную диаграмму сигнала , но частоты в не располагаются в зеркальном (обратном) порядке относительно несущей частоты .
Из этого
следует вывод: ширина
спектра АМ сигнала
равна удвоенному значению наиболее
высокой частоты
спектра модулирующего низкочастотного
сигнала, то есть
