Графики функций, заданных в параметрической форме

Построение графиков в полярной системе координат возможно двумя способами. Первый способ основан на использовании обычной декартовой системы координат. Координаты каждой точки при этом задаются в параметрическом виде: x = fx(t) и у =fy(t), где независимая переменная t меняется от минимального значения tmin до максимального tmах с шагом dt. Особенно удобно применение таких функций для построения замкнутых линий, таких как окружности, эллипсы, циклоиды и т. д. Например, окружность радиусом R может быть задана в следующей параметрической форме: х = R cos(t) и у = R sin(t), если t меняется от 0 до 2п. В общем случае радиус также может быть функцией параметра t.

Для построения параметрических заданных функций используются следующие графические средства:

ParametricPlot [{fx, fy}, {t, tmin, tmax}]—строит параметрический график с координатами f х и f у (соответствующими х и у), получаемыми как функции от t;

ParametricPlot [{{fx, fy}, {gx, gy},...}, {t, tmin, tmax}] —строит графики нескольких параметрических кривых.

Функции f x, f у и т. д. могут быть как непосредственно вписаны в список параметров, так и определены как функции пользователя.

Рисунок 8.12 показывает построение параметрических заданной фигуры Лиссажу. Она задается функциями синуса и косинуса с постоянным параметром R и аргументами, кратными t. Эти фигуры наблюдаются на экране электронного осциллографа, когда на его входы X и Y подаются синусоидальные сигналы с кратными частотами.

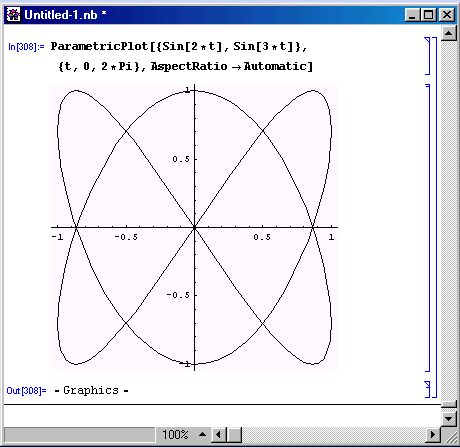
Рис. 8.12. Построение фигуры Лиссажу

На одном графике можно строить две и более фигур с заданными параметрических уравнениями. На рис. 8.13 показан пример такого построения — строятся две фигуры Лиссажу, причем одна из них является окружностью. Больше двух фигур строить нерационально, так как на черно-белом графике их трудно различить.

Теперь рассмотрим второй способ построения графиков в полярной системе координат (рис. 8.14). Здесь каждая точка является концом радиус-вектора R(t), причем угол t меняется от 0 до 2я. На рис. 8.14 функция R(t) задана как функция пользователя R[t_] с использованием образца t_ для задания локальной переменной t в теле функции.

Изменение параметра R позволяет заметно увеличить число отображаемых функций — фактически, их бесконечно много. Помимо описанной фигуры на рис. 8.14 дополнительно построена линия окружности единичного радиуса. Чтобы она имела правильные пропорции на экране, задана опция AspectRatio->l.

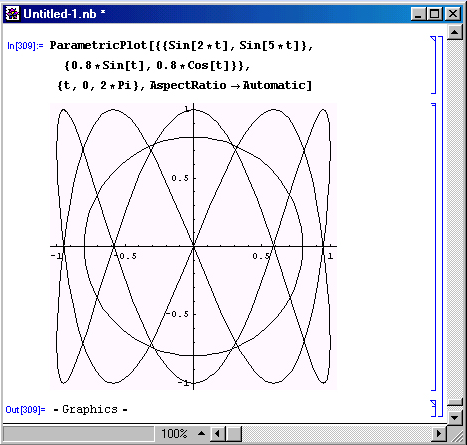
Рис. 8.13. Построение на одном графике двух фигур Лиссажу

Рис. 8.14. Построение графика функции в полярной системе координат

Трехмерная графика

Трехмерная графика, называемая также ЗО-графикой, представляет в аксонометрической проекции объемное изображение поверхностей или фигур, которые описываются либо функциями двух переменных, либо параметрически заданными координатами объектов. В данном разделе описаны многие способы построения трехмерных графиков, начиная от простых контурных графиков и кончая графиками поверхностей и фигур с функциональной окраской.