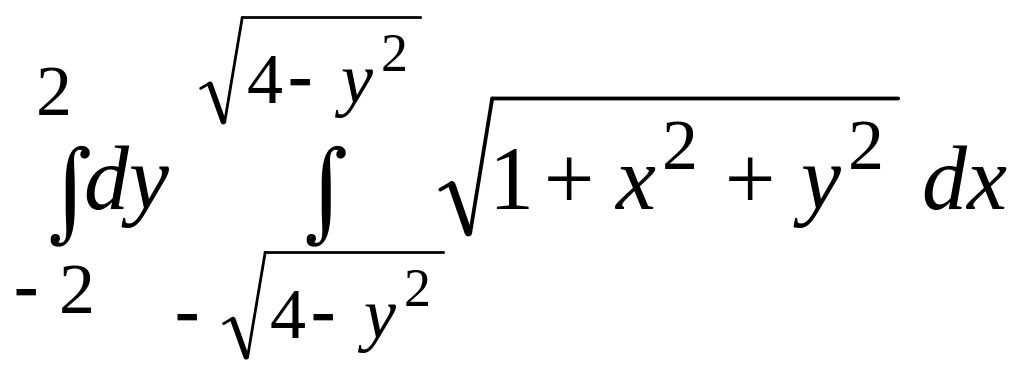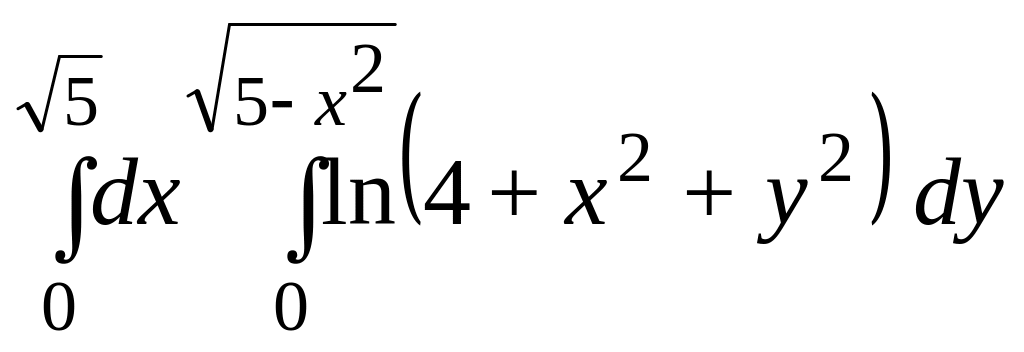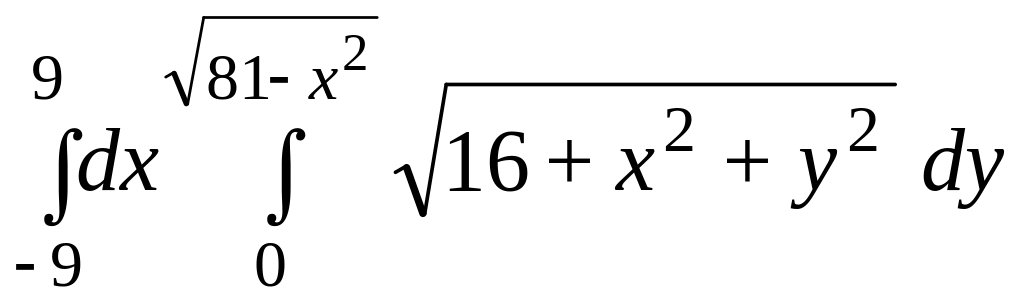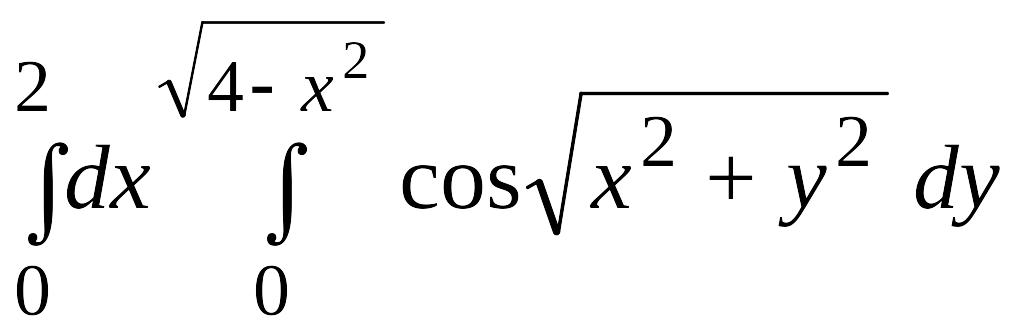- •1. Вычислите длину дуги кривой, заданной уравнением
- •2. Представьте двойной интеграл в виде повторного интеграла
- •3. Вычислите двойной интеграл, воспользовавшись переходом к полярным координатам
- •4. Вычислите площадь плоской области , ограниченной заданными линиями
- •5. Вычислите массу неоднородной пластины , ограниченной заданными линиями, если поверхностная плотность в каждой её точке
- •6. Вычислите объём тела V, ограниченного поверхностями
- •7. Вычислите объём тела V,
- •8. Вычислите массу неоднородного тела V, ограниченного поверхностями, если плотность в каждой её точке
- •9. А) Найдите градиенты скалярных полей , и угол между ними в точке м;
- •10. Найдите работу силы при перемещении вдоль а) линии l от точки а к точке в;
- •12. Найдите поток векторного поля через замкнутую поверхность s (нормаль внешняя)
1. Вычислите длину дуги кривой, заданной уравнением
1.1.
|
1.19.
|
1.2.
|
1.20.
|
1.3.
|
1.21.
|
1.4.
|
1.22.
|
1.5.
|
1.23.
|
1.6.
|
1.24.
|
1.7.
|
1.25.
|
1.8.
|
1.26.
|
1.9.
|
1.27.
|
1.10.
|
1.28.
|
1.11.
|
1.29.
|
1.12.
|
1.30.
|
1.13.
|
1.31.
|
1.14.
|
1.32.
|
1.15.
|
1.33.
|
1.16.
|
1.34.
|
1.17.
|
1.35.
|
1.18.
|
1.36.
|
2. Представьте двойной интеграл в виде повторного интеграла
а) с внешним интегрированием по х;
б) с внешним
интегрированием по
![]() ,
,
если область D ограничена указанными линиями.
2.1.
|
2.19.
|
2.2.
|
2.20.
|
2.3.
|
2.21.
|
2.4.
|
2.22.
|
2.5.
|
2.23.
|
2.6.
|
2.24.
|
2.7.
|
2.25.
|
2.8.
|
2.26.
|
2.9.
|
2.27.
|
2.10.
|
2.28.
|
2.11.
|
2.29.
|
2.12.
|
2.30.
|
2.13.
|
2.31.
|
2.14.
|
2.32.
|
2.15.
|
2.33.
|
2.16.
|
2. 34.
|
2.17.
|
2.35.
|
2.18.
|
|
3. Вычислите двойной интеграл, воспользовавшись переходом к полярным координатам
3.1.
|
3.19.
|
3.2.
|
3.20.
|
3.3.
|
3.21.
|
3.4.
|
3.22.
|
3.5.
|
3.23.
|
3.6.
|
3.24.
|
3.7.
|
3.25.
|
3.8.
|
3.26.
|
3.9.
|
3.27.
|
3.10.
|
3.28.
|
3.11.
|
3.29.
|
3.12.
|
3.30.
|
3.13.
|
3.31.
|
3.14.
|
3.32.
|
3.15.
|
3.33.
|
3.16.
|
3.34.
|
3.17.
|
3.35.
|
3.18.
|
3.36. |
4. Вычислите площадь плоской области , ограниченной заданными линиями
4.1. а)
б)
|
4.19. а)
б)
|
4.2. а)
б)
|
4.20. а)
б)
|
4.3. а)
б)
|
4.21. а)
б)
|
4.4. а)
б)
|
4.22. а)
б)
|
4.5. а)
б)
|
4.23. а)
б)
|
4.6. а)
б)
|
4.24. а)
б)
|
4.7. а)
б)
|
4.25. а)
б)
|
4.8. а)
б)
|
4.26. а)
б)
|
4.9. а)
б)
|
4.27. а)
б)
|
4.10. а)
б)
|
4.28. а)
б)
|
4.11. а)
б)
|
4.29. а)
б)
|
4.12. а)
б)
|
4.30. а)
б)
|
4.13. а)
б)
|
4.31. а)
б)
|
4.14. а)
б)
|
4.32. а)
б)
|
4.15. а)
б)
|
4.33. а)
б)
|
4.16. а)
б)
|
4.34. а)
б)
|
4.17. а)
б)
|
4.35. а) б)
|
4.18. а)
б)
|
4.36. а)
б)
|