
- •Раздел 4. Теория игр.
- •4.1. Понятие об игровых моделях.
- •4.2. Классификация игр.
- •4.3. Решение матричных игр в чистых стратегиях.
- •4.4. Смешанное расширение матричной игры.
- •4.5. Свойства решений матричных игр.
- •4.6. Графический метод решения игр и .
- •4.7. Сведение матричной игры к задаче линейного программирования.
- •4.8. Принятие решения в условиях неопределённости
- •4.8.1. Понятие о статистических играх
- •4.8.2. Критерии принятия решения
- •4.8.2.1. Критерий максимального математического ожидания выигрыша
- •4.8.2.2. Критерий недостаточного основания Лапласа
- •4.8.2.3. Максиминный критерий Вальда
- •4.8.2.4. Критерий минимаксного риска Сэвиджа
- •4.8.2.5. Критерий пессимизма-оптимизма Гурвица
- •4.8.2.6. Критерий Ходжа-Лемана
- •Пример.
- •4.9. Определение экономического эффекта информации с использованием методов теории игр
- •Пример.
- •4.10. Моделирование банковской деятельности «играми с природой».
- •A). Критерии, основанные на известных вероятностях условий
- •Б). Критерии, основанные на субъективной основе
- •В). Критерии крайнего пессимизма
- •4.11. Использование методов теории игр в предпринимательской деятельности.
- •4.12. Кооперативные игры.
- •4.12.1. Природа и структура кооперативных игр
- •4.12.2. Некоторые понятия решения кооперативной игры
- •4.12.2.1. С-ядро
- •4.12.2.2. Вектор Шепли
A). Критерии, основанные на известных вероятностях условий
Иногда неопределенность ситуации удается в некоторой степени ослабить. Это достигается нахождением вероятностей состояний на основе данных статических наблюдений.
Предположим, что вероятности состояний «природы» известны:
![]() .
.
Тогда
среднее значение (математическое
ожидание) выигрыша
![]() ,
которое игрок 1 стремится максимизировать,
определяется по формуле:
,
которое игрок 1 стремится максимизировать,
определяется по формуле:
![]() .
.
В
качестве оптимальной стратегии выбирается
та из стратегий
![]() ,
которая соответствует максимальному
среднему значению выигрыша:
,
которая соответствует максимальному
среднему значению выигрыша:
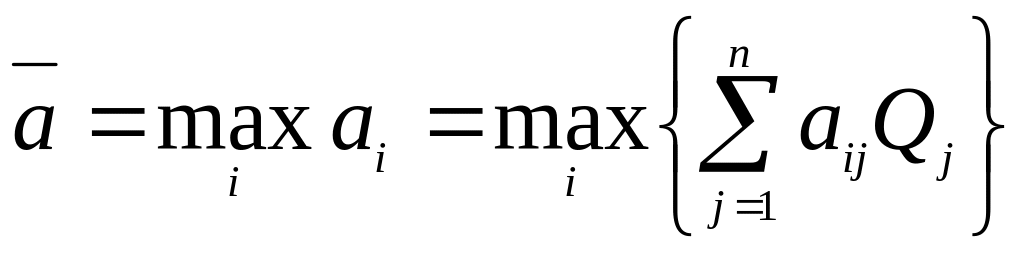 .
.
Оптимальную стратегию при известных состояниях «природы» можно найти, используя показатель риска. Для этого необходимо определить среднее значение риска:
![]() .
.
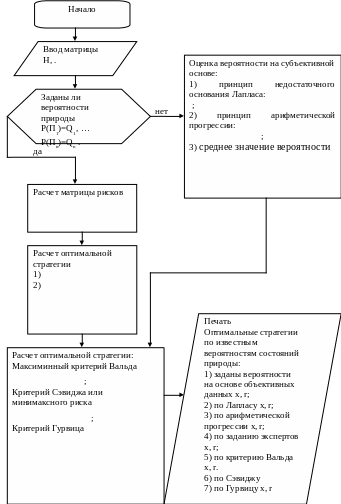
Рис.1.
В качестве оптимальной стратегии в данном случае выбирается та, которая обеспечивает минимальное среднее значение риска:
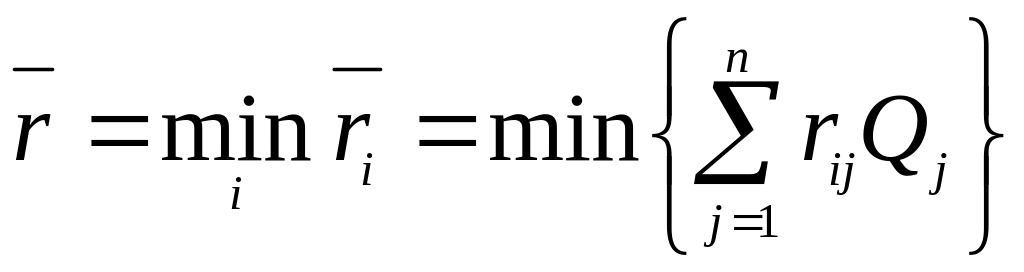 .
.
Замечание. Применение критериев среднего выигрыша и среднего риска для одних в тех же исходных данных приводит к одному и тому результату.
Отметим еще одно
важное положение, что когда известны
вероятности состояний природы
![]() .
игроку 1 нет смысла использовать смешанные
стратегии.
.
игроку 1 нет смысла использовать смешанные
стратегии.
Б). Критерии, основанные на субъективной основе
В случаях, когда объективные оценки состояний получить невозможно, оценки вероятности состояний природы могут быть сделаны на субъективной основе. В этом случае используются следующие принципы.
1. Принцип недостаточного основания Лапласа:
![]() ,
,
который применяется тогда, когда ни одного состояние природы нельзя предпочесть другому.
Для задачи о покупки банком валюты, принцип недостаточного основания Лапласа будет иметь следующий вид:
![]()
![]() .
.
2. Убывающая арифметическая прогрессия:
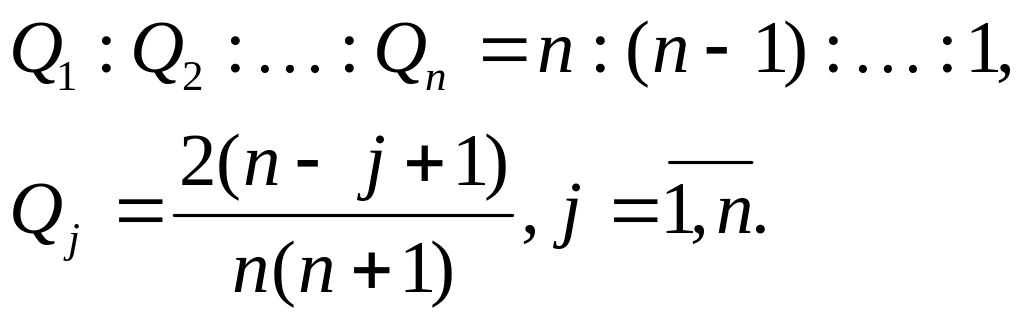
Этот прием применяется, если можно расположить состояния «природы» в порядке убывания их правдоподобности (вероятности свершения);
Для нашей задачи получим:
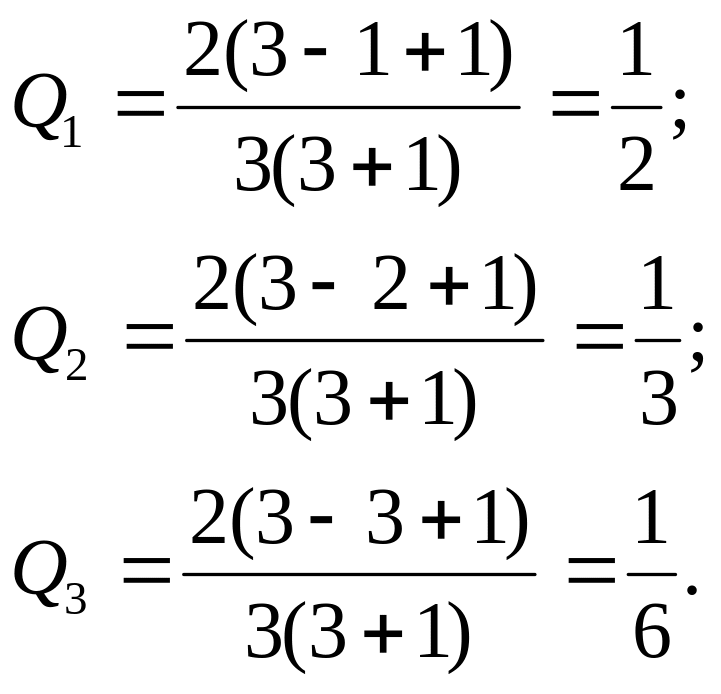
3.Получение
средних значений вероятностей состояний
![]() используя оценки группы экспертов.
используя оценки группы экспертов.
Рассчитаем
матрицу риска
![]() .
.
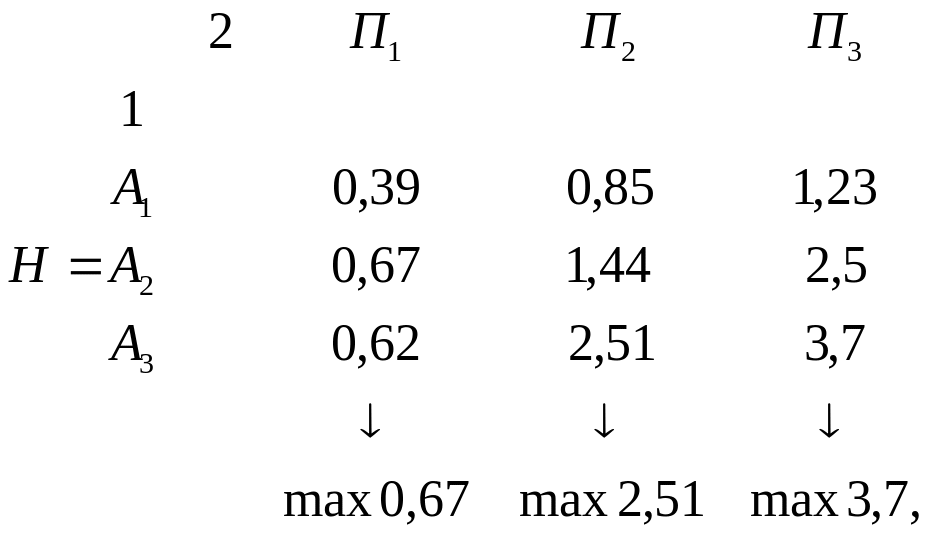 Получим:
Получим:
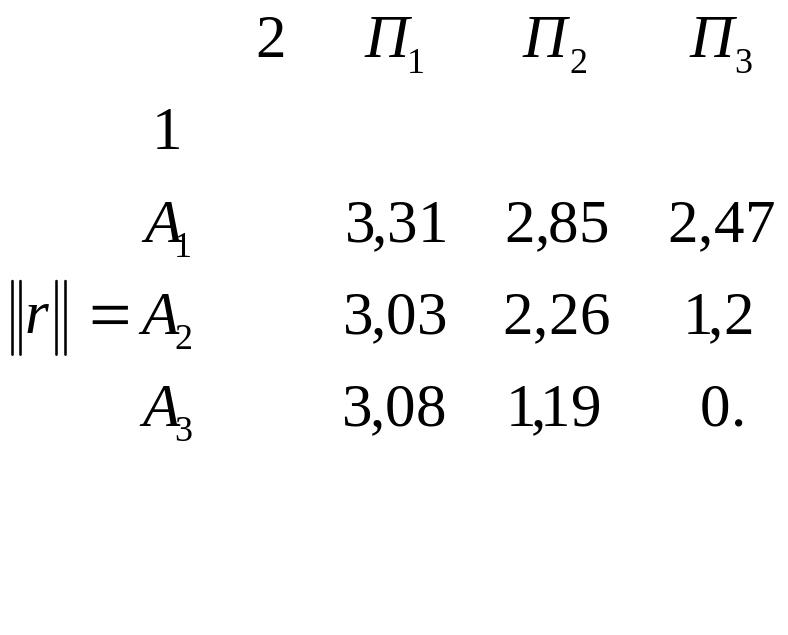
В). Критерии крайнего пессимизма
Кроме, рассмотренных подходов к решению игр с «природой», субъективно назначенных вероятностей состояний «природы» существуют и другие подходы к нахождению оптимального решения в полной неопределенности, основанные на применении других критериев.
Нахождение оптимального решения в условиях полной неопределенности. Максиминный критерий Вальда - критерий крайнего пессимизма. В соответствии с критерием крайнего пессимизма в качестве оптимальной рекомендуется выбирать ту стратегию, которая гарантирует в наихудших условиях максимальный выигрыш, т.е. максиминную стратегию:
![]() .
.

Оптимальной
стратегии соответствует стратегия
![]() .
.
Критерий Сэвиджа или минимаксного риска, также как и критерий Вальда, является критерием крайнего пессимизма. Согласно этому критерию рекомендуется выбирать ту стратегию, при которой в наихудших условиях величина риска принимает наименьшее значение:
![]()
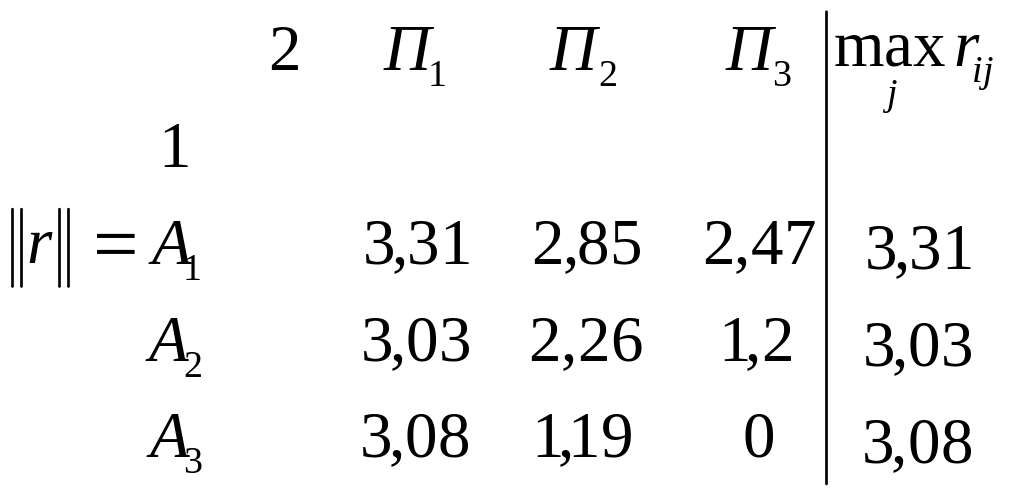
что
соответствует оптимальной стратегии
![]() .
.
Критерий Гурвица. Этот критерий называется критерием обобщенного максимума или пессимизма-оптимизма. Он имеет вид:
![]()
Очевидно,
что при
![]() критерий Гурвица превращается в
пессимистический критерий Вальда, а
при
критерий Гурвица превращается в
пессимистический критерий Вальда, а
при
![]() - в критерий крайнего оптимизма.
Коэффициент выбирается
на
основании субъективных соображений
(опыта, здравого смысла и т.д.).
- в критерий крайнего оптимизма.
Коэффициент выбирается
на
основании субъективных соображений
(опыта, здравого смысла и т.д.).
Если, например, взять:
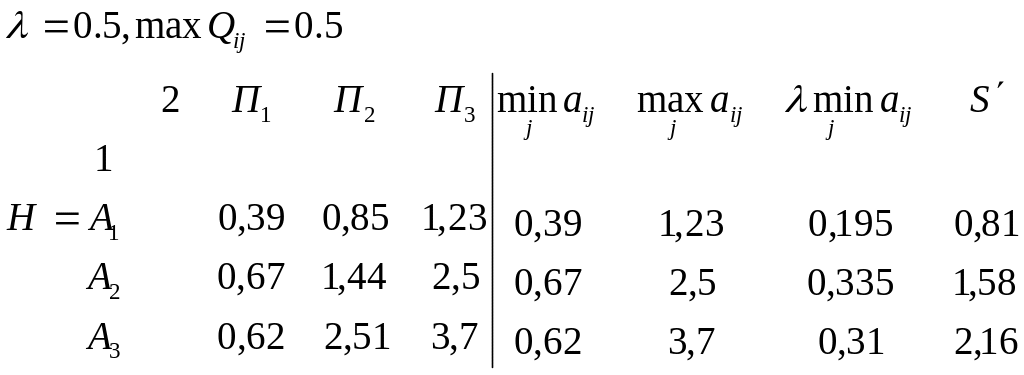
![]() ,
что соответствует стратегии
,
что соответствует стратегии
![]() .
.
Рассчитаем оптимальные стратегии на основе известных вероятностей «природы», валютного рынка:
Пусть
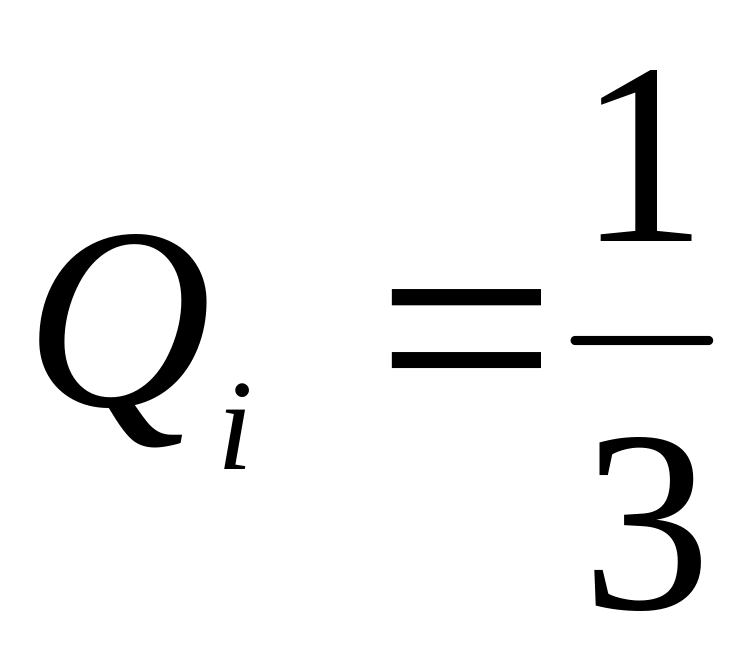 ,
тогда
,
тогда
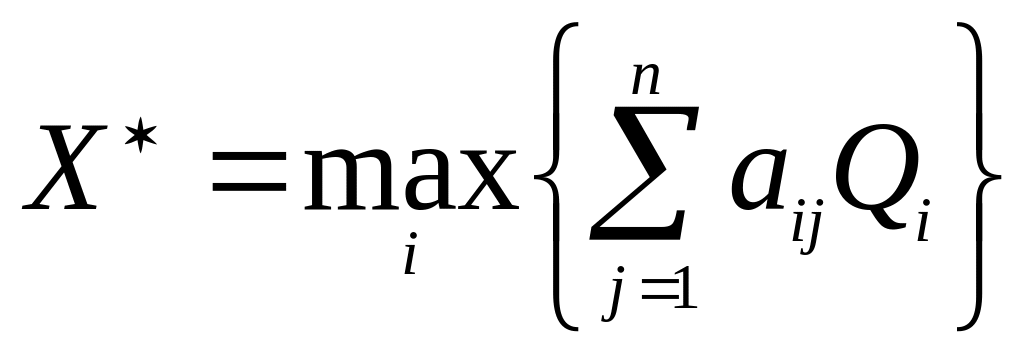 ,
,
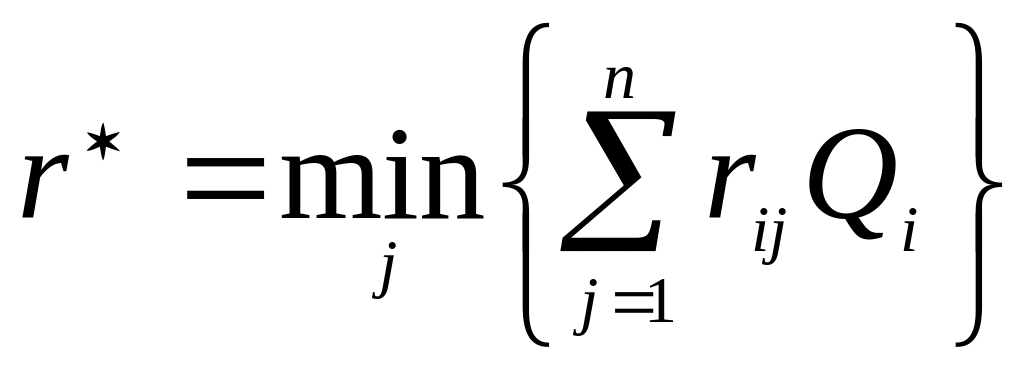 .
.
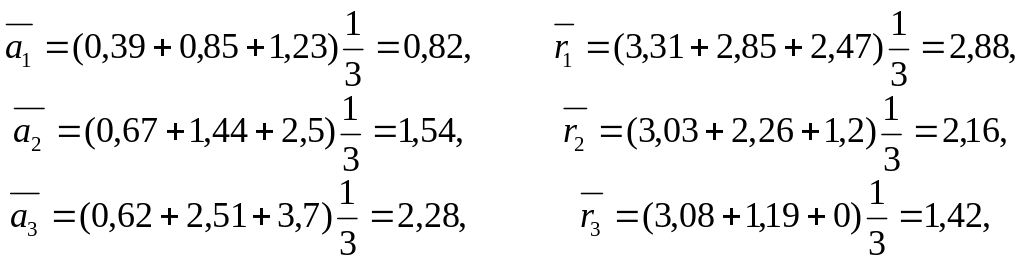
![]() ,
что соответствует стратегии
,
а
,
что соответствует стратегии
,
а
![]() ,
что также соответствует стратегии
.
,
что также соответствует стратегии
.
Пусть
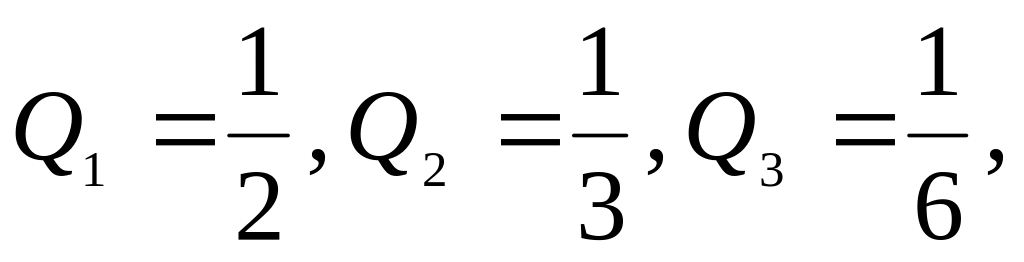 тогда
тогда
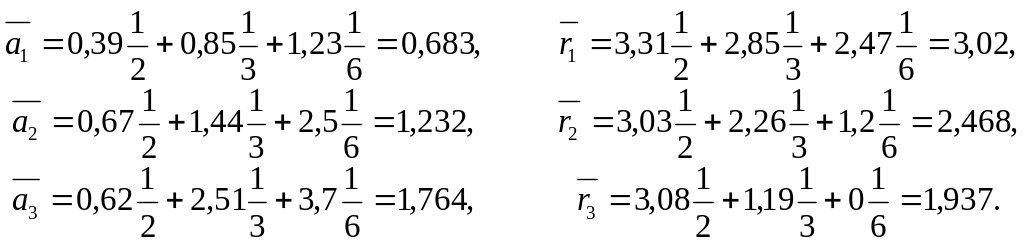
Оптимальной стратегии соответствует .
