20. Поняття степеневого ряду. Теорема Абелья. Інтервал та радіус збіжності степеневого ряду.

Озн: Степеневим рядом наз. Ф-ний ряд віду (1)

де , дійсні числа, які наз. коефіціентами ряду. Степеневим рядом за степеннями двохчлена наз. ф-ним рядом виду (2)

Зауваження 1: Заміною завжди можно перейти від степеневого ряду (2) до ряду (1) тому надалі будемо розглядати лише степеневі ряди вигляду (1)

Зауваження 2: Всякий степеневий ряд вигляду (1) завжди збіжний в точці х=0 і його сума Таким чином область збіжності ряду (1) завжди містить принаймні одну точку.

Теорема1(Абелья) Якщо степеневий ряд (1) збігаеться в точці то він абсолютно збігаеться для всіх

Теорема2(Абелья) Якщо ряд (1) розбіжний в точці то він буде розбіжним для всіх

Дов. Нехай степеневий ряд (1) збігаеться в точці тоді збіжним є числовий ряд в цьому віпадку виконуеться необхідна умова збіжності числового ряду

звідси випливае, що { } обмежена, тобто , що виконуеться нерівність розглянемо тепер точку х таку, що тоді велечина 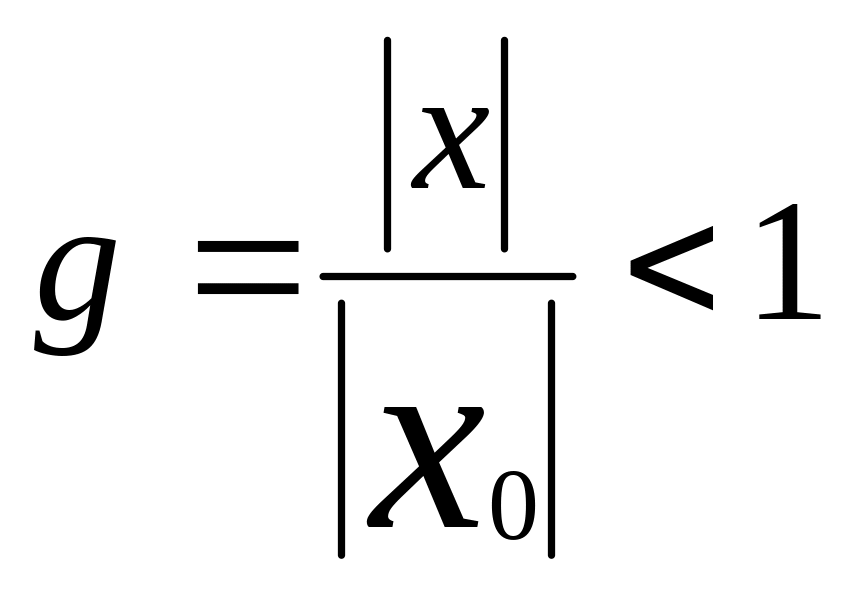Розглянемо 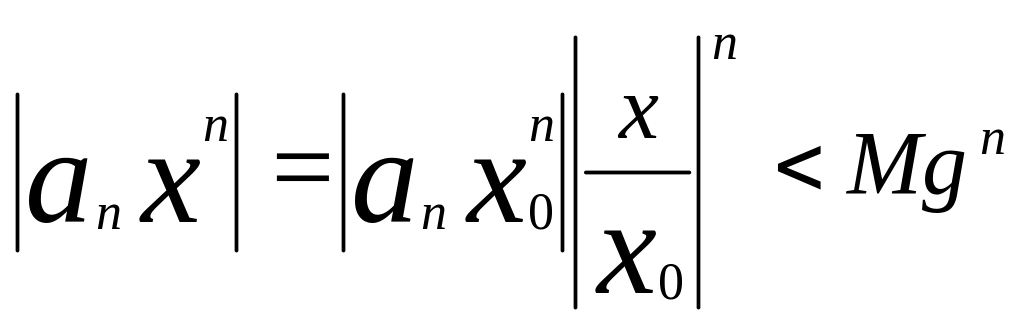Оскільки ряд збіжний, як геометрична прогресія (g<1) то за теоремою Верштрасе ряд абсолютно збіжні при Нехай ряд (1) розбігаеться в точці покажемо, що він розбіжний для всіх точок х таких що Припустимо супротивне тобто така, що і всякий степеневий ряд (1) збігаеться тоді за першим твердженням теореми Абелья степеневий ряд (1) повинен збігатися і в точці , а це суперечить умові теореми.

Наслідок: Для області збіжності степеневого ряду можливі три випадки

1. Степеневий ряд (1) збігаеться лише в точці х=0

2. Степеневий ряд (1) збігаеться при всіх

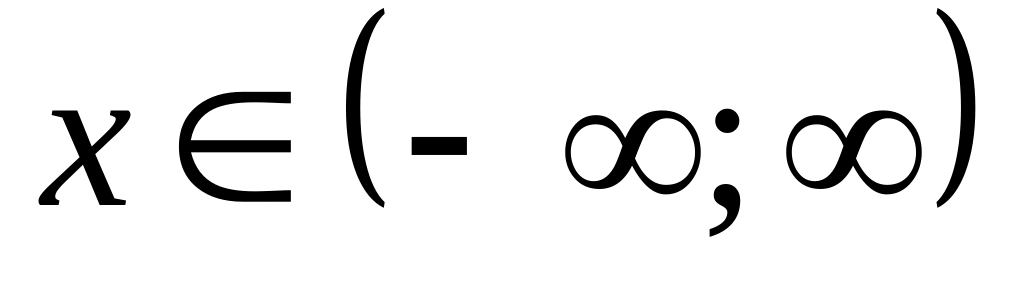
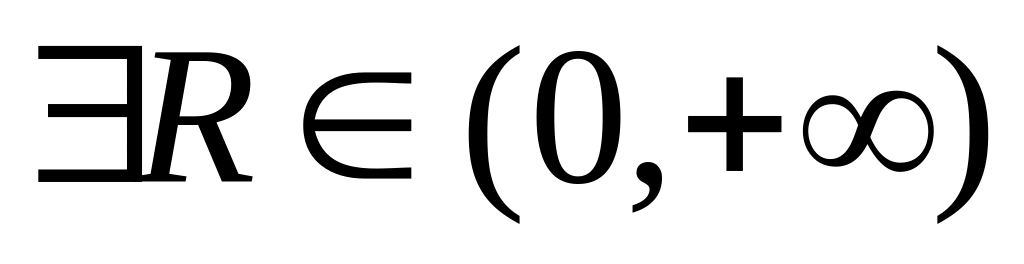
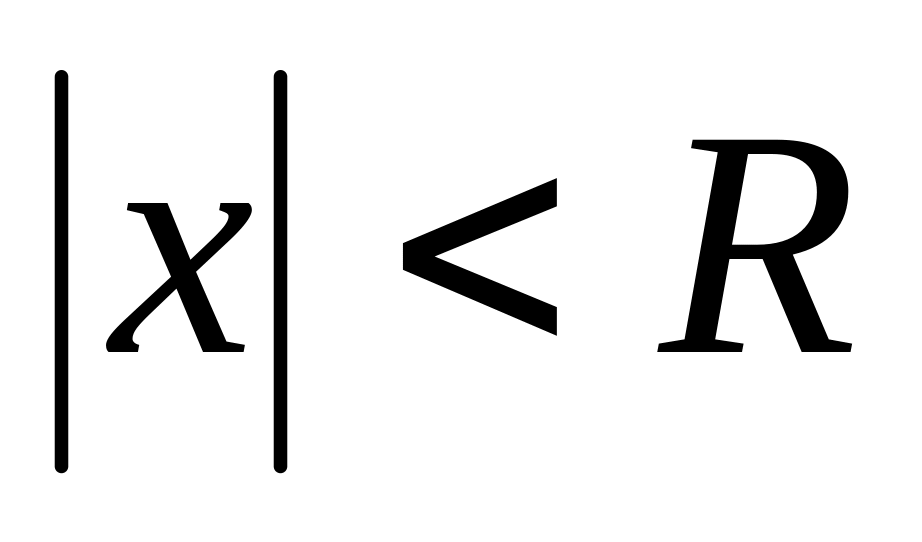3. - збігаеться і розбігается

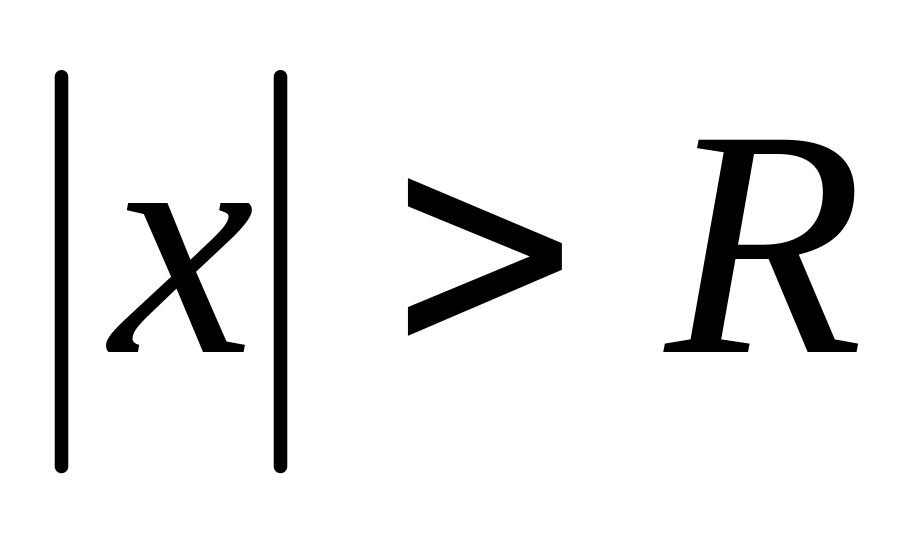
Озн: Число R наз. радіусом збіжності степеневого ряду (1) , а інтервал (-R;R) наз. інтервалом збіжності цього ряду.

Розглянемо спосіб визначення радіуса збіжності степеневого ряду . Розглянемо ряд складений ряд з модулів членів ряду (1) Припустимо, що існуе границя ₌

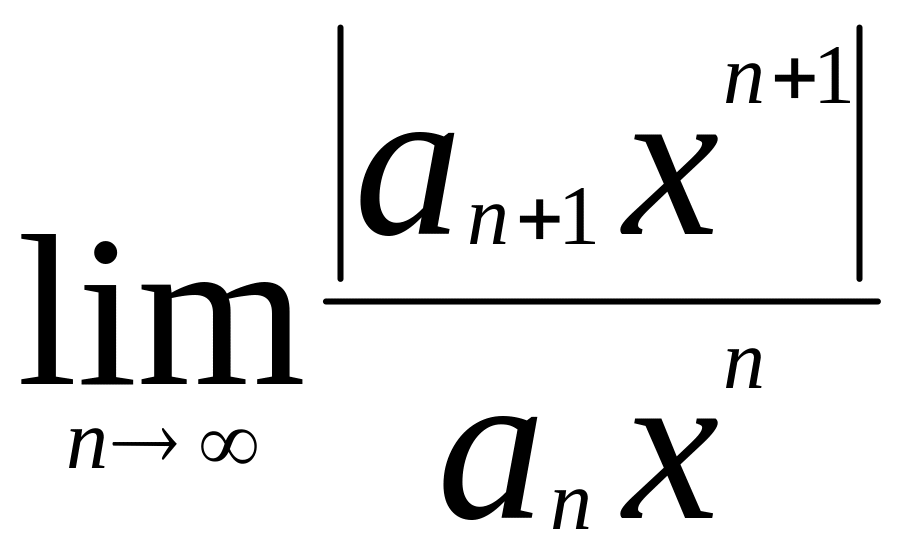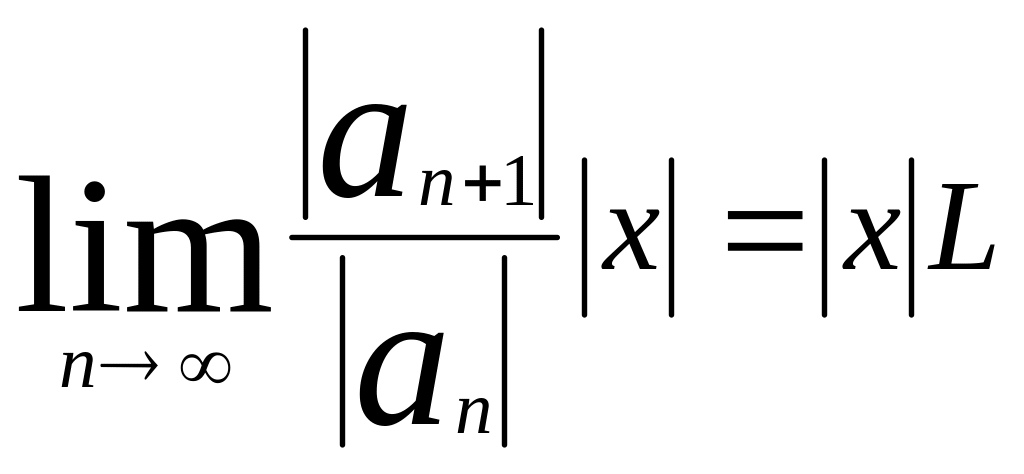, Тоді за ознакою Долонбера ряд (1) збігаеться, якщо або

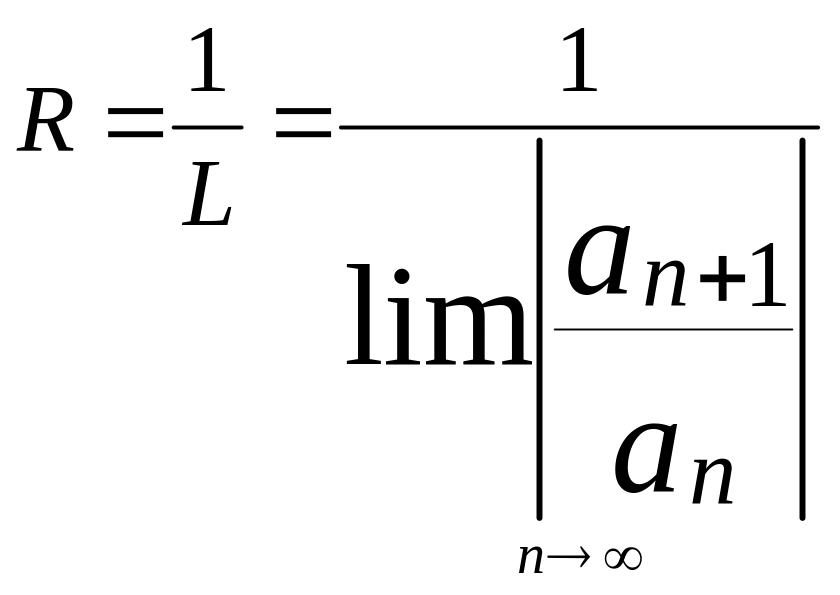
тобто інтервал збіжності є , арадіус збіжності є число 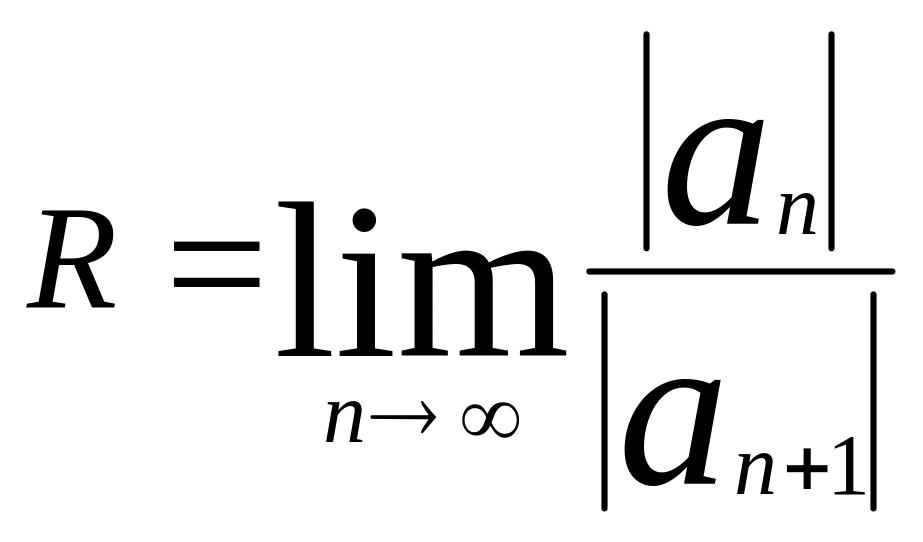(3)

Даний ряд розбігаеться, якщо тобто аналогічно, використовуючи ознаку Коші, можна довести, що радіус збіжності степеневого ряду (1) 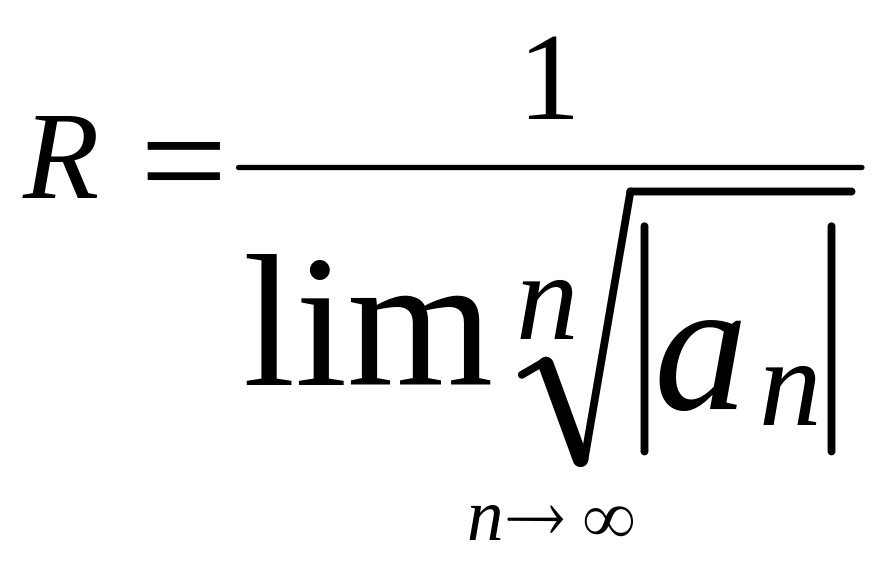(4)

Зауваження1: У випадку коли _{L=0 R= ряд (1)} збігаеться на всій числовій осі.

У випадку коли L= _R= областю збіжності ряду (1) є точка х=0.

Зауваження2: Інтервалом збіжності степенеого ряду (1) є (-R;R) але питання про збіжність ряду треба для кожного степеневого ряду розвязувати окремо. Таким чином область збіжності степеневого ряду (1) ьщже видризнятися від (-R;R) хіба лише двома точками .

Зауваження3: Для степеневого ряду (2) радіус зближеності знаходять за такими ж ф-ми (3) і(4) , що і для ряду (1) , а інтервал збіжності визначають з нерівності R тобто він мае вигляд

21. Схема исследования области сходимости степ. Ряда. Примеры. Свойства степ. Рядов

Рассм: (1), (2). Схема исследования : 1) по формулам или найти радиус сходимости. 2) Найти инт. сходимости для (1) (-R;R), для (2) (x₀-R; x₀+R) 3)В предельных точках интервала сходимости иссл. соотв. числовые ряды. 4) Граничные точки в которых соотв. числовые ряды сходятся присоед. В интервал сходимости. Пример1:Найти обл. сходимости ряда ⁼ . Интервал сходимости (-1;1). Если х=-1 имеем Этот знакоперем ряд сходящийся по признаку Лейбница. Если х=1 - расходящийся. Таким образом обл. сходимости этого ряда [-1;1). Пример2: Радиус сходимости R=1. (x₀-R; x₀+R)=(-3-1;-3+1)=(-4;2). Х=-4: ряд сходится по призн. Лейбница . Х=-2: обобщ гармонич. Ряд сходящийся. Таким образом обл. сходимости данного ряда промежуток [-4;-2]. Свойства степенных рядов :

1)степ ряд абсолютно и равномерно сходящийся на отрезке Док-ство: Поск ρ<R рассм по усл сходится. Тогда потому по призн. Вейерштрасса ряд (1) – абсол. И равномерно содящийся на 2)Сумма степ. Ряда (1) непр. Внутри его интервала сходимости Это св-во следует из св 1) м св-в (1)-(5) функц. Рядов. 3)Если пределы инт. α и β лежат внутри интервала (-R;R) то на отрезке [α;β ] этот ряд можно почленно интегрировать . В частности если ряд (1) интегрировать на [0;x], |x|<R , то в рез. Получим степ ряд который имеет тот самый интервал сходимости что и (1). Если сумму (1) обозн через , то 4) Если ряд (1) имеет интервал сходимости (-R;R) то ряд слож. Из производных членов ряда (1) имеет тот самый интервал сходимости. Кроме того . Замечание : таким образом на отрезке [a;x], |x|<R ряд (1) можно сколько угодно интегрировать, а сколько угодно дифер. При этом полученные ряды имеют тот же инт. Сходимости что и ряд (1).

Пример: обозн. Сумму через S(x). Ее можно рассм как геометр. Прогрессию с a=1 n q=x² тогда интегрируя на [0;x] , |x|<1

получим

таким образом