
- •19.Функціональні ряди поняття рівномірной збыжн. Озн вейерштр.
- •20. Поняття степеневого ряду. Теорема Абелья. Інтервал та радіус збіжності степеневого ряду.
- •Теорема2(Абелья) Якщо ряд (1) розбіжний в точці то він буде розбіжним для всіх
- •21. Схема исследования области сходимости степ. Ряда. Примеры. Свойства степ. Рядов
- •22. Ряд Тейлора
- •23. Разложение элементарн. Функций в ряд Макларена
- •24. Тригонометрический ряд Фурье.
- •25. Ряды Фурье для функций четных и нечетных. Ряды Фурье для 2l периодических функций. Примеры.
- •26. Подвійний інтеграл умови його існування і властивості
- •28. Заміна змінних в подвійному інтегралі.Подвійний інтеграл у полярних координатах.
- •29. Поняття потрійного інтегралу. Умови його існування та властивості.
- •30. Обчислення потрійного інтегралу. Приклади.
- •31. Заміна зміних у потрійному інтегралі.
- •32. Криволінійні інтеграли. Приклади.
- •33. Деякі застосування кратних та криволінійних інтегралів.
19.Функціональні ряди поняття рівномірной збыжн. Озн вейерштр.
Озн:
Нехай {![]() }
}![]() n=1
послідовність функції визначено на
деякій числовій множині Е . Функціональним
рядом називають вираз
n=1
послідовність функції визначено на
деякій числовій множині Е . Функціональним
рядом називають вираз
![]()
![]() (1).
Візьмемо точку Х0
(1).
Візьмемо точку Х0![]() і у ряді (1) покладемо Х=X0
одержемо числовий ряд
і у ряді (1) покладемо Х=X0
одержемо числовий ряд
![]()
![]() (2).
(2).
Ряд (2) може бути як збіжним так і розбіжним.
Озн-я: Якщо ряд(2) збігається, точка Х0 –точка збіжності функціонального ряду (1). Якщо ряд (2) розбігається то точка Х0 – точка розбіжності функціонального ряду множини всіх точок збіжності функціонального ряду (1) називається областю збіжності цього ряду.
Зауваження: Зрозуміло , що область збіжності ряду(1) може ,як співпадати з множиною Е так і становити деяку її частину.
Оз-ня:
N-ю
частиною сумою функціонального ряду
(1) називають вираз
![]()
![]() В
кожній точці Х ,яка належить області
збіжності ряду(1) існує скінченна границя
В
кожній точці Х ,яка належить області
збіжності ряду(1) існує скінченна границя
![]()
цю границю
називають сумою ряду (1) і пишуть
![]()
![]()
![]() -
визначена в області збіжності
функціонального ряду (1).
-
визначена в області збіжності
функціонального ряду (1).
Оз-ня: N- нним залишком функціонального ряду(1) називають вираз
![]()
![]()
зрозуміло,
що для всіх точок Х з області збіжності
ряду(1)
![]()
![]()
Зауваження: Відомо, що сума скінченого числа неперервной ф-й є ф-ю неперервною.Крім того сума скінченого числа ф-ї, можно почлено диференцюювати та інтегрувати. (якщо існують відповідні похідні і інтеграли). Виявляеться, що властивості незавжди виконуються для суми нескінченого числа доданків для ф-них рядів. Однак всі ці властивості зберігаються для так званих рівномірно збіжних ф-них рядів.
Оз-ня:
Ф-ний ряд (1) наз. збіжним на деякій
множині D![]() E,
якщо
E,
якщо
![]() існуе N=N(E)
і незалежить від Х, що виконуеться для
існуе N=N(E)
і незалежить від Х, що виконуеться для
![]() n>N,
n>N,
![]()
![]() D
D![]() /
/![]() (х)/<
(х)/<![]() E.
E.
Основні властивості рівномірного збіжних ф-них рядів:
Якщо членами ф-ного ряду (1) є неперервні ф-цій на деякій множині D і цей ряд рівномірно збігаеться то його сума є ф-ю неперервною на множині D.
Якщо ф-ний ряд (1) рівномірно збігаеться на [a;b] і його члени є неперервні на цому відрізку ф-й то ряд (1) можна почлено інтегрувати у межах [
 ,
,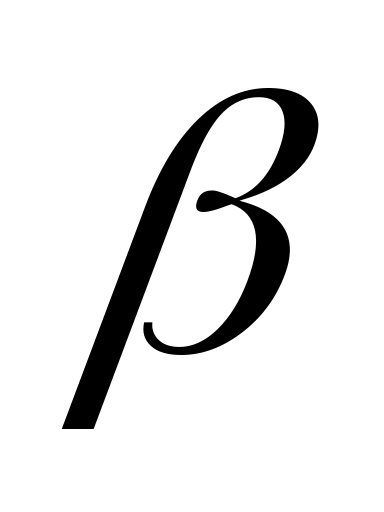 ]
[a,b]
тобто:
]
[a,b]
тобто:
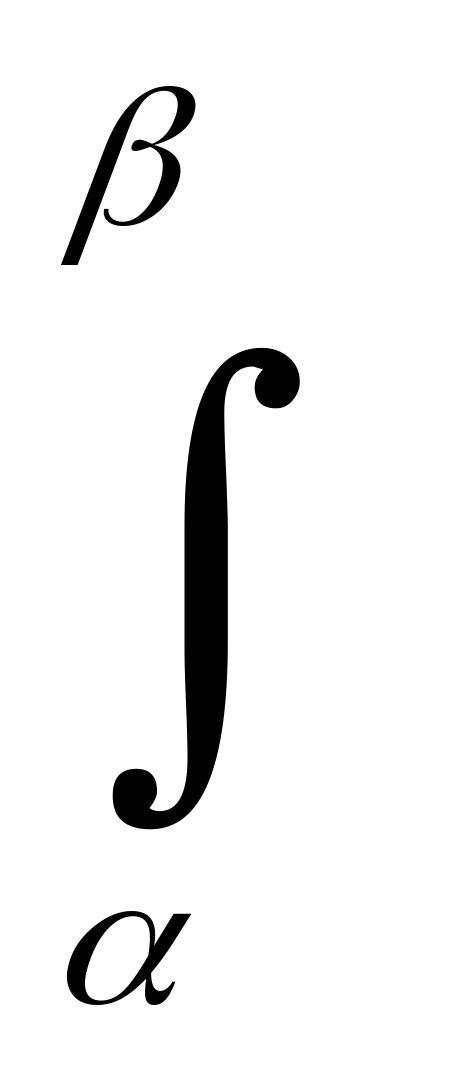 S(х)dx=
S(х)dx=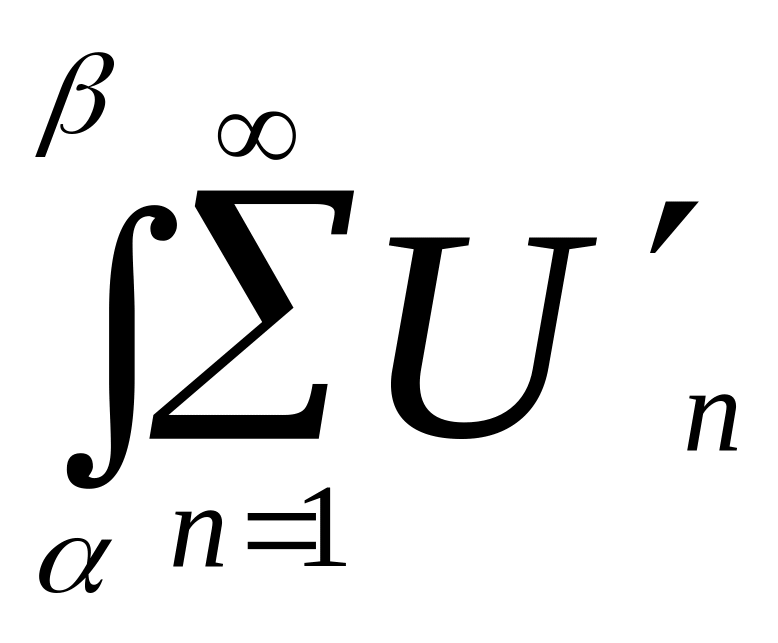 (x)dx=
(x)dx=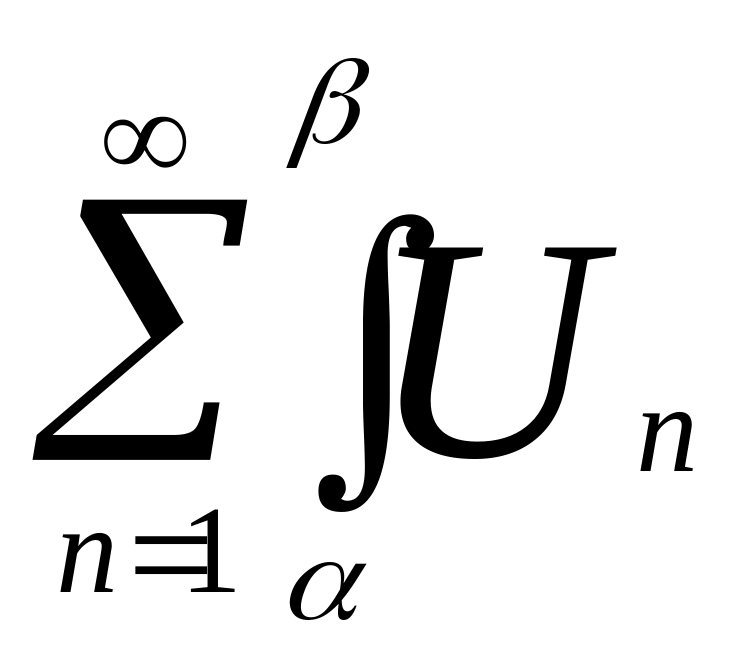 (x)dx
(x)dxЯкщо ряд (1) збігаеться на відрізку [a;b] а ряд складених з його похідних
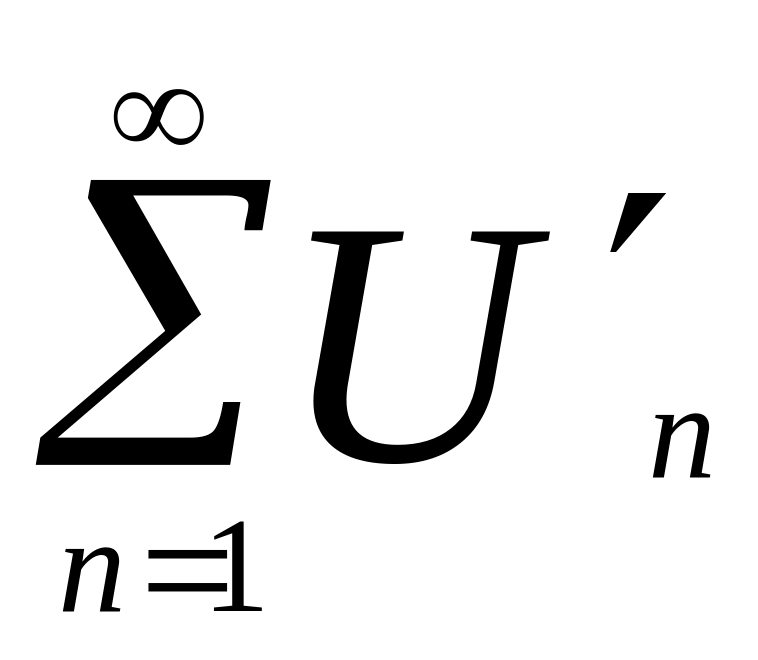 (х)
(х)
рівномірно
збігаеться на [a;b]
і крім того ф-й [a;b],
![]() /N
то ряд (1) можна почлено диференцюювати,
тобто:
/N
то ряд (1) можна почлено диференцюювати,
тобто:
![]() (x)=
(x)=![]() =
=![]() ,
[a;b]
,
[a;b]
Теорема:
(Ознака Верштрасе) Ф-ний ряд один абсолютно
і рівномірно, зберігаеться на [a;b]
, якщо для
/N
виконуеться нерівність /![]() /
/![]() ,
х
[a;b]
де ряд
,
х
[a;b]
де ряд
![]() збіжний додатній числовий ряд.
збіжний додатній числовий ряд.
Дов. З
умови три і ознаки порівняння випливае,
що ряд (1) є абсолютно збіжним на відрізку
[a;b]
. Покажемо теперь рівномірну збіжність
ряду (1) . Оскільки ряд (1) абсолютно
збігаеться то абсолютним буде його
залишок:
![]() =
=![]()
![]()
![]() ,
,
де
![]() -n-ий
залишок ряду
-n-ий
залишок ряду
![]() відомо,
що коли числовий ряд
збігаеться його залишок при n
відомо,
що коли числовий ряд
збігаеться його залишок при n![]() прямуе до 0.Дісно, якщо
прямуе до 0.Дісно, якщо
![]()
![]()
n
, тоді
![]() >0
>0
![]() >N
>N![]() E
Звідси для всіх
E
Звідси для всіх
![]() виконуеться нерівність /
(х)/<E
Це означае, що ряд (1) є рівномірно збіжним
на [a;b]
виконуеться нерівність /
(х)/<E
Це означае, що ряд (1) є рівномірно збіжним
на [a;b]
Приклад:
Дослідити на рівномірну збіжність ф-ий
ряд:
![]()
![]() виконуеться нерівність
виконуеться нерівність
![]() Ряд
Ряд
![]() збігаеться за ознакою Доломбера:
збігаеться за ознакою Доломбера:
![]() ,
,
![]()
g=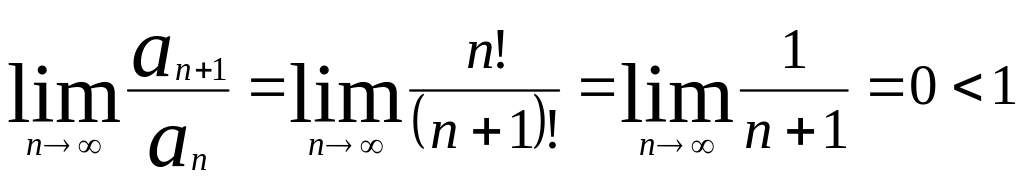
Таким чином вказаний ф-ний ряд рівномірно збігаеться за ознакою Верштрасе на всій числовій осі.
