Питання для самоперевірки та вправи

1. Знайти максимальний потік в транспортній мережі:

3

10

11

4

8

11

s

t

2

4

5

2

2. Алгоритм знаходження найкоротшого шляху між двома заданими вершинами.

3. Знайдіть найкоротший шлях між вершинами s і t:

14

15

21

7

18

17

5

s

9

15

11

t

8

10

44

16

5

41

Лекція №27 Побудова дерева найкоротших шляхів. Транспортна задача

Для знаходження найкоротшого шляху між вершинами використовуємо співвідношення

(27.1)

де - це вершина, що безпосередньо передує вершині в найкоротшому шляху від до .

Якщо існує декілька найкоротших шляхів від до будь-якої іншої вершини, то при деякій фіксованій вершині співвідношення (27.1) буде виконуватися більше, ніж для одної вершини . В цьому випадку вибір може бути довільним, або таким, що розглядаються усі дуги , які входять в якийсь з найкоротших шляхів.

Знайдемо найкоротший шлях від і . Для цього знаходимо вершину з співвідношення:

В стовпці, що відповідає вершині в матриці, представленої таблицею 11.1 і в останній стрічці таблиці 11.2 знаходимо числа, сума яких дорівнює 5.

В стовпці таблиці 11.1 є числа 10, 18, 2, 13. Беремо найменше з них – це 2, яке відповідає вершині .

. Таким чином, задовольняє співвідношенню 12.1.

Знаходимо тепер вершину , що безпосередньо передує вершині . Вершина повинна задовольняти умові:

.

В стовпці таблиці 11.1 знаходяться числа 3, 2, 4, 14, 24. Беремо найменше з них – це 2, йому відповідає вершина :

. Беремо наступне найменше число

. Отже, найкоротший шлях від до - це шлях .

Знайдемо найкоротший шлях від до . По таблиці 11.2 . В матриці 11.1 в стовпці є числа 18, 25, 20. Беремо 18, що відповідає вершині :

.

Але найкоротший шлях від до вже побудовано на попередньому кроці, отже:

Знайдемо найкоротший шлях від до

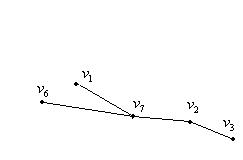
Таким чином будується дерево найкоротших шляхів для будь-якої іншої вершини.

Транспортна задача

Серед задач пошуку максимального потоку в практиці значне місце посідають задачі найбільш раціонального розподілу потоків по дугах транспортної мережі. Такі задачі носять назву транспортних.

У випадках, коли транспортна мережа становить схему організації перевезень будь-яких вантажів, розв’язання транспортної задачі повинно дати відповідь про найбільш раціональний з точки зору певного критерію план перевезень або розподіл маршрутів. Серед можливих критеріїв, які повинні задовольнити розв’язання транспортної задачі, можуть бути, наприклад, економічний (мінімальна вартість перевезень), часовий (доставка в найкоротший час) тощо.

Транспортна задача з критерію мінімальної вартості перевезень в термінах теорії графів формулюється так. Дано транспортну мережу з найбільшим потоком , потік , який повинен бути забезпечений по ній, пропускні спроможності окремих дуг, а також вартість проходження одиниці потоку по кожній дузі .

Необхідно знайти такий розподіл потоку по дугах транспортної мережі, який забезпечує мінімальну вартість його транспортування з вершини у вершину . При цьому для кожної дуги повинно виконуватися співвідношення:

, а вартість проходження потоку по дузі дорівнюватиме добутку . При розв’язанні цієї задачі будемо розглядати величини , тобто як довжини відповідних дуг.

У цьому випадку вартість проходження потоку по будь-якому шляху буде дорівнювати добутку довжини цього шляху на величину потоку і задача зводиться до задачі знаходження найкоротшого шляху.

Якщо нема обмежень на пропускну спроможність дуг, то найкоротшим буде той шлях, який забезпечує мінімальну вартість проходження потоку. Якщо є такі обмеження, то задача розв’язується в декілька етапів.

Загальний шлях розв’язання задачі.

У графі , що зображує транспортну мережу з довжинами дуг , відшукується найкоротший шлях і пропускна спроможність .

По цьому шляху пропускається потік:

Якщо , задача розв’язана і шлях є найбільш економічним для потоку .

Якщо , потік вважається частковим і переходимо до графа , який отримуємо з графа шляхом заміни пропускних спроможностей дуг

У такому разі дуги, в яких з розгляду виключаються. Потік, розподілення якого тепер відшукується в графі : .

Отже, повертаємося до попередньої задачі пошуку найекономічнішого розподілу потоку на графі .

Розв’язання цієї задачі дає найекономічніший шлях з пропускною спроможністю , через який пропускається частковий потік:

Якщо - задача розв’язана, якщо переходимо до графа і так далі.

Цей процес треба повторювати доти, поки сума часткових потоків не досягне значення . Ці часткові потоки дають найекономічніший розподіл потоку .

s

a

c

b

t

8/5

5/4

15/8

6/5

5/8

5/2

20/8

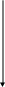
Наприклад: У графі знайти найекономічніший шлях перевезень вантажів з вершини у вершину , якщо .

Вартість перевезень та пропускна спроможність зазначена на дугах – x/y, де х - вартість перевезень, а y - пропускна спроможність.

Розв’язок:

У графі знайдемо найкоротший шлях з вершини у вершину . Таким шляхом буде - (s,a), (a,b), (b,t). =2 < . Вартість перевезень часткового потоку . Переходимо до графа при цьому дуга (a,b) з розгляду виключається:

. Потік, який відшукується в графі

. Найкоротший шлях з вершини у вершину тепер буде - (s,b), (b,t). =3 < . Вартість перевезень часткового потоку .

Оскільки переходимо до графа

; - (s,a),(a,с), (с,t). < . Вартість перевезень часткового потоку .

.

Переходимо до графа , потік, який відшукується: .

- (s,b), (b,c), (c,t) , отже, задача розв’язана. .

Найекономнішим буде шлях, вартість перевезень по якому для заданої мережі буде: грошових одиниць.