
- •1. Закони геометричної оптики. Використовуючи принцип Ферма доведіть закони відбивання та заломлення світла.
- •2.Інтерференція світлових хвиль. Отримайте умови інтерференційних максимумів та мінімумів для різниці фаз та оптичної різниці ходу.
- •3.Дослід Юнга. Отримайте формули для координат максимумів та мінімумів інтенсивності світла. Знайдіть ширину інтерференційних смуг.
- •4. Інтерференція світла при відбиванні від тонких пластин. Виведіть формули для максимумів та мінімумів інтенсивності.
- •5. Кільця Ньютона. Отримайте формули для радіусів світлих та темних кілець у відбитому світлі.
- •6. Дифракція світла. Принцип Гюйгенса-Френеля та його фізичне обґрунтування.
- •7. Зони Френеля. Доведіть формулу для радіуса зони Френеля.
- •8. Дифракція Френеля від круглого отвору
- •9. Дифракція Френеля від круглого диску
- •10. Дифракція Фраунгофера від щілини
- •11. Дифракційна гратка.
- •12. Кутова та лінійна дисперсія.
- •13. Критерій Релея. Ф-ла роздільної здатності.
- •14. Дифракція рентгенівських променів. Формула Вульфа-Брегга
- •Вопрос 22: Дисперсія світла. Дисперсія речовини. Нормальна та аномальна дисперсія.
- •Вопрос 23: Поглинання світла, закон Буггера. Розсіяння світла, закон Релєя.
- •Вопрос 24: Теплове випромінювання. Закон Кірхгофа.
- •Вопрос 25: Закон Стефана-Больцмана. Закон зміщення Віна.
- •Вопрос 26: Формула Релэя-Джинса, ультрафіолетова катастрофа. Формула Планка.
- •Вопрос 27: Фотоефект. Формула Ейнштейна для зовнішнього фотоефекта, червона межа фотоефекта.
- •Вопрос 28: Визначення сталої Планка методом затримуючого потенціалу.
11. Дифракційна гратка.
Дифракційною решіткою називається оптичний прилад, який складається з великої кількості однакових щілин, розділених між собою однакової ширини непрозорими проміжками. Відстань d між серединами двох сусідніх щілин, називається сталою дифракційної решітки.
Якщо розмістити паралельно решітці збірну лінзу, то в її фокальній площині на екрані можна буде спостерігати результати дифракції світла від решітки (рис.4).
Оптична різниця ходу променів від двох сусідніх щілин дорівнює
 (21)
(21)
Оптична різниця фаз в цьому випадку буде дорівнювати
 (22)
(22)
В
точку P
на екрані приходять промені від усіх
щілин. Всі ці промені зсунуті по фазі
на однакову величину
 .
.
Для знаходження результуючої амплітуди всіх хвиль, які прийшли в точку Р слід скористатися формулою результуючої амплітуди при інтерференції багатьох хвиль
 (23)
(23)

Рис. 4
З
урахуванням (22) результуюча амплітуда
 буде дорівнювати
буде дорівнювати
 (24)
(24)
де
 – амплітуда хвиль від однієї щілини;
– амплітуда хвиль від однієї щілини;
 – число щілин у решітці;
– число щілин у решітці;
 – стала дифракційної решітки;
– стала дифракційної решітки;
 – довжина хвилі монохроматичного
світла.
– довжина хвилі монохроматичного
світла.
Проведемо аналіз формули (24).
а) Якщо вираз у знаменнику (24) досягає мінімуму, тобто буде дорівнювати нулю, то амплітуда буде найбільшою. Ця умова є умовою максимуму дифракції на дифракційній решітці, тобто
 ,
,
звідки
 . (25)
. (25)
Формула (25) є умовою головних максимумів дифракції на дифракційній решітці.
б) Побічні максимуми дифракції можна одержати, якщо чисельник у формулі (24) досягає максимуму. Це можливо за умови, коли
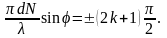 (26)
(26)
Після скорочення одержимо
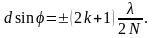 (27)
(27)
Вираз (27) є умовою побічних максимумів дифракції на дифракційній решітці.
в) Побічні мінімуми дифракції на дифракційній решітці одержуємо із умови коли чисельник формули (25) буде найменшим, тобто коли
 (28)
(28)
звідки
 (29)
(29)
Формула (29) є умовою побічних мінімумів на дифракційній решітці.
12. Кутова та лінійна дисперсія.
Кожна дифракційна решітка характеризується кутовою дисперсією, яка позначається буквою Д
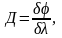 (30)
(30)
де
 – кутова відстань між спектральними
лініями, які відрізняються за довжиною
хвилі на величину
– кутова відстань між спектральними
лініями, які відрізняються за довжиною
хвилі на величину
 .
.
Для
знаходження кутової дисперсії дифракційної
решітки слід продиференціювати формулу
головних максимумів дифракції
 ,
тобто
,
тобто

звідки

В
межах невеликих кутів
 ,
тому можна вважати, що
,
тому можна вважати, що
 (31)
(31)
Таким чином кутова дисперсія обернено пропорційна періоду решітки d. Чим вищий порядок спектра k, тим більша дисперсія.
Лінійною дисперсією називають величину
 ,
,
де
dl
– лінійна відстань на екрані між двома
максимумами одного й того самого порядку
m
для хвиль
і
 .
.
Якщо фокусна відстань лінзи, у фокальній площині якої спостерігається дифракційна картина, дорівнює F, то
 і
і
 .
.
13. Критерій Релея. Ф-ла роздільної здатності.
Для
дифракційної гратки Релей запропонував
такий критерій спектрального розділення:
спектральні лінії з довжинами хвиль
і
 вважаються розділеними, якщо головний
максимум дифракційної картини для хвилі
довжиною
збігається за своїм розміщенням з першим
дифракційним мінімумом того самого
порядку для хвилі довжиною
вважаються розділеними, якщо головний
максимум дифракційної картини для хвилі
довжиною
збігається за своїм розміщенням з першим
дифракційним мінімумом того самого
порядку для хвилі довжиною
 ,
а інтенсивність в проміжку між максимумами
становить не більше ніж 80% від інтенсивності
максимуму (рис. 235).
,
а інтенсивність в проміжку між максимумами
становить не більше ніж 80% від інтенсивності
максимуму (рис. 235).

Нехай
головний максимум m-го
порядку для хвиль
знаходиться на місці першого мінімуму
 спектра того самого порядку для хвилі
:
спектра того самого порядку для хвилі
:
 ,
,
 .
.
Звідси
 ,
,
тобто
 .
.
Роздільна здатність гратки
 .
.
Отже, роздільна здатність гратки пропорційна порядку спектра m і кількості N щілин.
Оскільки
 ,
а
,
а
 ,
то
,
то
 ,
,
де
 – максимальний кут дифракції і
– максимальний кут дифракції і
 .
Тому, максимальна роздільна здатність
гратки буде
.
Тому, максимальна роздільна здатність
гратки буде
 .
.
