4. Постановка задачі

Для досягнення мети необхідно:

1. Вивчити предметну область;

2. Провести огляд аналогів;

3. Навчити нейронну мережу, за допомогою утиліт що поставляються бібліотекою OpenCV, та отримати на виході каскад Хаара.

4. Розробити метод автоматизованого розпізнавання об’єктів на базі алгоритмів контурного аналізу.

5. Розробити програмний продукт, в якому використовуються два методи детектування об'єктів за допомогою «Контурного аналізу» та «Каскаду Хаара».

6. Провести аналіз ефективності детектування обох методів. Скласти таблицю ефективності з отриманих результатів.

5. Об’єкт та методи дослідження

У своїй магістерській роботі я буду орієнтуватися на мову програмування Java, зокрема на бібліотеку JavaCV (оболонка бібліотеки OpenCV). Ця бібліотека володіє потужними засобами для обробки зображень. Бібліотека є хорошим інструментом розробки, дослідження і моделювання методів і алгоритмів обробки зображень. При вирішенні задач обробки зображень цей пакет дозволяє йти двома шляхами. Перший з них полягає в самостійній програмної реалізації методів і алгоритмів. Інший шлях дозволяє моделювати рішення задачі за допомогою готових функцій, які реалізують найбільш відомі методи та алгоритми обробки зображень. І той, і інший спосіб виправданий. Але все ж для дослідників та розробників методів і алгоритмів обробки зображень більш переважнішим є другий шлях.

У тому та іншому підході об'єктом дослідження є зображення. Я буду орієнтуватися на растрові зображення, які представляють собою двовимірний масив, елементи якого (пікселі) містять інформацію про колір. Надалі, при розгляді методів обробки зображень, будемо вважати, що зображення представляється матрицею чисел (розмір матриці N * M), де значення кожного елемента відповідає певному рівню квантування його енергетичної характеристики (яскравості). Це так звана піксельна система координат.

Обробка зображень здійснюється рекурсивними і не рекурсивними методами. Рекурсивні методи використовують результат обробки попереднього пікселя, не рекурсивні - не використовують. В більшості випадків використовуються не рекурсивні алгоритми обробки зображень.

Обробка зображень є багатоплановою задачею. Сюди включають рішення задач фільтрації шумів, геометричної корекції, градаційної корекції, посилення локальних контрастів, різкості, відновлення зображень та ін.

Одним із підходів до обробки зображення з метою покращення його візуальної якості для подальшого виявлення його границь є безпосереднє використання різних фільтрів. В залежності від специфікації шумів можуть застосовуватися різні способи фільтрації, фільтр на основі перетворення Гауса в даному випадку використовується для того, щоб зменшити паразитні сигнали.

Модель фільтра представлена ​​нижче:

(5.1)

Тут u - відстань по осі X, v - по осі Y, а σ - відхилення розподілу Гауса. Радіус розмиття можна отримати за формулою: (5.2).

Рівняння формує концентричні кола з розподілом Гауса від центру. Значення кожного пікселя усереднюється по відношенню до сусідніх в залежності від відстані. Вихідний піксель приймає більшу вагу, ніж сусідні. Для досягнення достатньої точності розрахунок проводиться на відстані не більше 3σ. Відповідно програма розраховує матрицю [6σ] х [6σ].

Спільна з методами виділення країв зображення, в задачі пошуку корисної інформації застосовуються смугові фільтри з обмеженим носієм, які призначені для відфільтровування верхніх частот. Відомі також алгоритми лінійної низькочастотної фільтрації, наприклад, фільтрація ковзким середнім, експоненціальна і медіанна фільтрація. Проте дані фільтри погано придушують дрібні, але контрастні утворення, а також змащують границі - розширюють смугу граничних точок. Тому в даній роботі використовується порогів фільтр cvThreshold [21-22].

(5.3)

Тут src () - це матриця вихідного зображення, x - позиція по горизонталі, y - позиція по вертикалі, threshold - заданий нами поріг, dst () - матриця нового зображення.

cvThreshold «зрізає» пікселі з яскравістю нижче заданої межі threshold встановлюючи їх яскравість в 0, а всіх інших у 255. Принцип роботи фільтра показано на малюнках: Рисунок 5.1 та Рисунок 5.2.

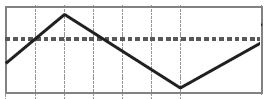
Рисунок 5.1 – До фільтрації фільтром cvThreshold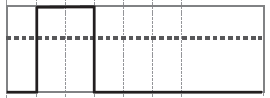

Рисунок 5.2 – Після фільтрації фільтром cvThreshold

Для підкреслення меж використовується оператор Canny. Оператор Canny використовує фільтр який може бути добре наближений до першої похідної Гауссіан σ = 1.4. Розглянемо математичну модель оператора:

(5.4)

Межі відзначаються там, де градієнт зображення набуває максимальне значення. Вони можуть мати різні напрямки, тому алгоритм Canny використовує чотири фільтра для виявлення горизонтальних, вертикальних і діагональних ребер в розмитому зображенні.

(5.5)

(5.6)

Кут напряму вектора градієнта округляється і може приймати такі значення: 0, 45, 90, 135. Відповідно рисунку 5.3

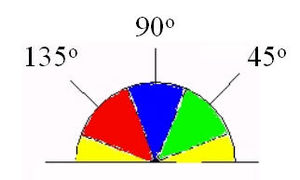
Рисунок 5.3 – Напрямок градієнта

Рисунок 5.4 – Початкове зображення

Рисунок 5.5 – Зображення на виході оператора Canny

Знайдені границі можна описати за допомогою моментів, таким чином можна відмовитися від обробки кожної точки зображення і перейти до обробки самих контурів.

Момент - це характеристика контуру, об'єднана (просумовона) з усіма пікселями контуру. Момент (p, q) визначається за формулою (5.7):

(5.7)

Тут p - порядок x, q - порядок y, де порядок означає, так би мовити, потужність, на якій відповідний компонент узятий в сумі з іншими відображеними.

Момент можна описати у вигляді структури:

typedef struct CvMoments{

// просторові моменти

double m00, m10, m01, m20, m11, m02, m30, m21, m12, m03;

// центральні моменти

double mu20, mu11, mu02, mu30, mu21, mu12, mu03;

double inv_sqrt_m00;

} CvMoments;

Центральні моменти обчислюються за формулою (5.8):

(5.8)

де и .

Центральні моменти можна нормалізувати. Нормалізовані моменти обчислюються наступним чином:

(5.9)

Ну і залишилися ще інваріантні моменти. Ідея тут у тому, що комбінуючи різні нормалізовані центральні моменти, можливо створювати інваріантні функції, що представляють різні аспекти зображення, які не залежать від масштабів, обертання і відображення.

У документації до OpenCV наведені такі формули:

(5.10)

(5.11)

(5.12)

(5.13)

(5.14)

(5.15)

(5.16)

Щоб визначити ступінь схожості контурів, необхідно порівняти їх моменти. Для порівняння моментів існують наступні формули:

(5.17)

(5.18)

(5.19)

За формулами видно що, чим менший результат ми отримуємо від функції, тим вища ступінь схожості контурів.

Параметри и розраховуються по наступних формулах:

(5.20)

(5.21)

Де - інваріантні моменти першого контуру, - інваріантні моменти другого контуру.