Метод surf
SURF вирішує дві задачі - пошук особливих точок зображення і створення їх дескрипторів, інваріантних до масштабу і обертанню. Це означає, що опис ключової точки буде однаково, навіть якщо зразок змінить розмір і буде обернутий. Крім того, сам пошук ключових точок володіє інваріантністю. Так, що повернений об'єкт сцени має той же набір ключових точок, що і зразок.
Метод шукає особливі точки за допомогою матриці Гессе. Детермінант матриці Гессе (т.зв. гессіан) досягає екстремуму в точках максимальної зміни градієнта яскравості. Він детектує плями, кути і краї ліній. На рисунку 2.2.1 зображені особливі точки зображення будівлі, знайдені за допомогою матриці Гессе. Діаметр кола показує масштаб особливої точки, а зелена лінія - напрямок градієнта яскравості.
Рисунок 2.2.1 – Особливі точки зображення будівлі
Гессіан інваріантний до обертання. Але не інваріантний масштабу. Тому SURF використовує різномасштабні фільтри для знаходження гессіанів. Для кожної ключової точки розраховується напрямок максимальної зміни яскравості (градієнт) і масштаб, взятий з масштабного коефіцієнта матриці Гессе. Градієнт в точці обчислюється за допомогою фільтрів Хаара.
Після знаходження ключових точок, SURF формує їх дескриптори. Дескриптор являє собою набір з 64 (або 128) чисел для кожної ключової точки. Ці числа відображають флуктуації градієнта навколо ключової точки. Оскільки ключова точка являє собою максимум гессіан, то це гарантує, що в околиці точки повинні бути ділянки з різними градієнтами. Таким чином, забезпечується дисперсія (відмінність) дескрипторів для різних ключових точок.
Флуктуації градієнта околиць ключової точки розраховуються відносно направлення градієнта навколо точки в цілому (по всій околиці ключової точки). Таким чином, досягається інваріантність дескриптора щодо обертання. Розмір області, на якій розраховується дескриптор, визначається масштабом матриці Гессе, що забезпечує інваріантність щодо масштабу.
Флуктуації градієнта також розраховується за допомогою фільтра Хаара.
На рисунку 2.2.2, зліва знаходиться зразок, справа - сцена. Червоні лінії показують максимально схожі особливі точки зразка і сцени. Червона трапеція - показує виявлений на сцені об'єкт.
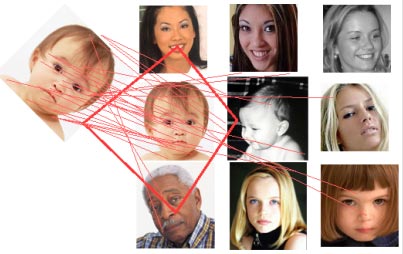
Рисунок 2.2.2 – Приклад роботи SURF
Метод sift
Виявлення об'єктів за допомогою методу SIFT полягає в порівнянні зображень по ключових точках.
Схема рішення задачі порівняння зображень:
На зображеннях виділяються ключові точки і їх дескриптори.
За збігом дескрипторів виділяються відповідно один одному ключові точки.
На основі набору ключових точок що співпали будується модель перетворення зображень, за допомогою якого з одного зображення можна отримати інше.
Основним моментом у детектуванні особливих точок є побудова піраміди гаусіан (Gaussian) і різниць гаусіан (Difference of Gaussian, DoG). Гаусіаном (або зображення розмите гаусовим фільтром) є зображення. Різницею гаусіанів називають зображення, отримане шляхом попіксельного віднімання одного гаусіана вихідного зображення від гаусіани з іншим радіусом розмиття [31].
Інваріантність щодо масштабу досягається за рахунок знаходження ключових точок для вихідного зображення, взятого в різних масштабах. Для цього будується піраміда гаусіанів: весь масштабований простір розбивається на деякі ділянки - октави, причому частина масштабованого простору, займаного наступної октавою, в два рази більше частини, займаної попередньої. До того ж, при переході від однієї октави до іншої робиться ресемплінг зображення, його розміри зменшуються вдвічі. Звісно, що кожна октава охоплює безліч гаусіанів зображення, тому будується тільки деяка їх кількість N, з певним кроком по радіусу розмиття. З тим же кроком добудовуються два додаткові гаусіани (всього виходить N +2), що виходять за межі октави. Масштаб першого зображення наступної октави дорівнює масштабу зображення з попередньої октави з номером N.
Паралельно з побудовою піраміди гаусіанів, будується піраміда різниць гаусіанів, що складається з різниць сусідніх зображень в піраміді гаусіанів [31]. Відповідно, кількість зображень в цій піраміді буде N +1.
На рисунку 2.3.1 зліва зображена піраміда гаусіанів, а праворуч - їх різниця. Схематично показано, що кожна різниця виходить з двох сусідніх гаусіанів, кількість різниць на одиницю менше кількості гаусіанів, при переході до наступної октаві розмір зображень зменшується вдвічі.
Рисунок 2.3.1 – Піраміда гаусіанів
Точка вважається особливою, якщо вона є локальним екстремумів різниці гаусіанів. Для пошуку екстремумів використовується метод, схематично зображений на рисунку 2.3.2.
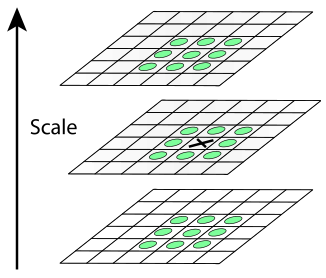
Рисунок 2.3.2 – Особлива точка
Якщо значення різниці гаусіанів в точці поміченої хрестиком, більше або менше за всіх значень в точках, позначених зеленими кружальцями, то ця точка вважається точкою екстремуму.
У методі SIFT дескриптором є вектор. Як і напрямок ключової точки, дескриптор обчислюється на гаусіані, що є найближчою за масштабом до ключової точки, і виходячи з градієнтів в деякому вікні ключової точки. Перед обчисленням дескриптора це вікно повертають на кут напрямку ключової точки, чим і досягається інваріантність щодо поворотів.
.
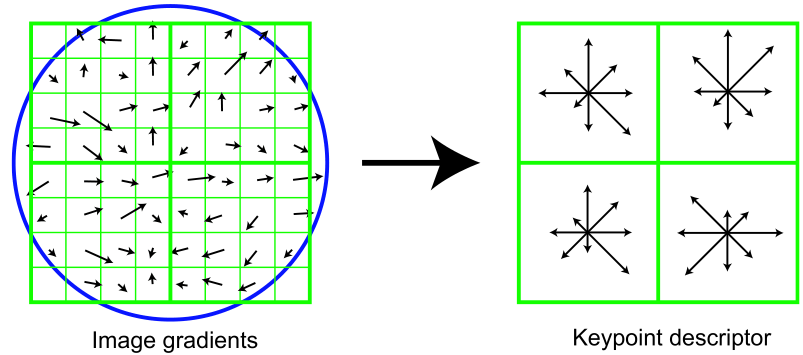
Рисунок 2.3.3 – Дескриптор ключових точок
Отриманий дескриптор нормалізується, після чого всі його компоненти, значення яких більше 0.2, урізуються до значення 0.2 і потім дескриптор нормалізується ще раз. У такому вигляді дескриптори готові до використання.
SIFT дескриптори не позбавлені недоліків. Не всі отримані точки і їх дескриптори будуть відповідати вимогам, що пред'являються. Звісно це буде позначатися на подальшому вирішенні задачі порівняння зображень. У деяких випадках рішення може бути не знайдено, навіть якщо воно існує. Наприклад, при пошуку афінних перетворень (або фундаментальної матриці) за двома зображеннями цегляної стіни, рішення може бути не знайдено через те, що стіна складається з повторюваних об'єктів (цеглин), які роблять схожими між собою дескриптори різних ключових точок. Незважаючи на цю обставину, дані дескриптори добре працюють в багатьох практично важливих випадках.