2. Предположим, что , . Исключаем источник эдс (закарачиваем) и находим частичный ток (рис.5.4б): .

3. Находим полный ток . Знак "минус" тока объясняется тем, что его направление не совпадает с положительным направлением тока в данной схеме.

5.4 Теорема компенсации

Теорема формулируется так: токи в электрической цепи не изменятся, если любое сопротивление заменить источником ЭДС, величина которого равняется спаду напряжения на этом же ребре, а направление противоположно направлению тока в ребре.

Правильность теоремы компенсации вытекает из того, что любое из слагаемых (падений напряжений), которые составляют уравнения по второму закону Кирхгофа, может быть перенесенно в другую сторону уравнения с противоположным знаком, т.е. рассматривается как дополнительная ЭДС, направленная навстречу току. Например, для схемы (рис.5.3а) можно записать такое уравнение:

, или .

Соответственно к последнему уравнению, схема будет выглядеть иначе (рис.5.3б), т.е. дополнительный источник можно рассматривать как зависимый источник напряжения.

Зависимый источник напряжения  источник ЭДС, в котором величина ЭДС зависит от тока или напряжения другого участки цепи.

6 Теорема об эквивалентном источнике

Теорема об эквивалентном источнике (генераторе) применяется тогда, когда надо определить ток в одной ветке сложной цепи. С помощью этой теоремы сложная электрическая цепь с произвольным количеством источников электрической энергии приводится к одноконтурной или двухузловой схеме с единым источником, благодаря чему расчет цепи упрощается. Существует два варианта теоремы.

6.1 Теорема о эквивалентном источнике напряжения (теорема Тевенена)

Любой линейный активный двуполюсник можно заменить эквивалентным источником напряжения с ЭДС, которая равняется напряжению холостого хода на зажимах двуполюсника, и внутренним сопротивлением, которое равняется входному сопротивлению пассивного двуполюсника.

Схематично активный и пассивный двуполюсники показаны на рис.6.1а. Работа в режиме холостого хода (цепи или генератора) означает работу в ненагруженном состоянии, когда выходной ток равняется нулю.

а) б)

Рисунок 6.1

Итак, согласно с теоремой, является целесообразной эквивалентная замена (рис.6.1б), причем , . По принципу эквивалентности внешние токи (напряжения) не изменяются: ток в нагрузке одинаковый для обеих схем . Для второй схемы

. (6.1)

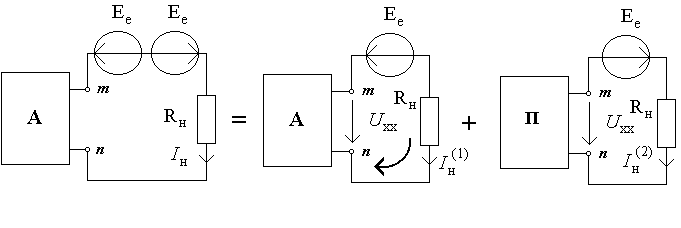
Рассмотренная теорема приходится в такой способ: для определения тока первой схемы к ветки mn вводятся две равные и противоположно направленные ЭДС , которые равняются напряжению холостого хода (рис.6.2а). Применение метода наложения согласно рис.6.2а приводит к выводу: . Для схемы (рис.6.2б) по второму закону Кирхгофа составим уравнение , из которого будем иметь значение первого частичного тока нагрузки, учитывая, что : ; .

а) б) в)

Рисунок 6.2

Для схемы (рис.6.2в) по закону Ома с учетом замены пассивного двуполюсника входным сопротивлением , будем иметь . Итак,

. (6.2)

Сравнивая (6.1) и (6.2) для любого значения тока, получаем значение параметров эквивалентного генератора напряжения: ; . Теорема доказана.

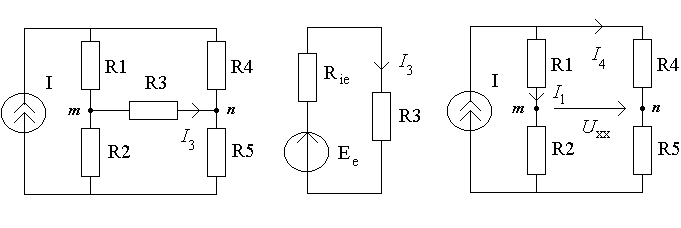
Пример 1. По теореме Тевенена определить ток в ребре (рис.6.3а).

а) б) в)

Рисунок 6.3

Решение задачи состоит из таких этапов:

1. заменяем активный двуполюсник относительно узлов m, n эквивалентным источником напряжения с параметрами , (рис.6.3б);

2. определяем значение ЭДС , как напряжение холостого хода при размыкании для схемы (рис.6.3в):

; ;

; ;

3. рассчитываем входное сопротивление пассивного двуполюсника со стороны узлов m, n (напомним, что для перехода от активного к пассивному двуполюснику необходимо идеальные источники ЭДС разомкнуть, а идеальные источники тока сомкнуть):

; ;

3. рассчитываем искомый ток по закону Ома по схеме (рис.6.3б):

.

6.2 Теорема об эквивалентном источнике тока (теорема Нортона)

Любой линейный активный двуполюсник можно заменить эквивалентним источником тока, заданый ток которого равняется току короткого замыкания между зажимами двуполюсника, и внутренним сопротивлением, какое равняется входному сопротивлению пассивного двуполюсника.

Режим короткого замыкания (цепи или генератора) означает работу в ненагруженном состоянии, когда выходное напряжение равняется нулю, а выходные зажимы закорочены.

Итак, по теореме Нортона должны быть эквивалентными две схемы (рис.6.4а). При условии , соответственно с принципом эквивалентности должно выполняться равенство .

а) б)

Рисунок 6.4

Доказательство. Воспользуемся результатами теоремы Тевенена. Для этого заменим источник тока источником напряжения (рис.6.4б). Пусть ; . Тогда согласно с (3.7) . (6.3)

Эта формула определяет не что другое, как ток, который проходит между выводами m и n, которые замкнуты накоротко (ток короткого замыкания): .

Искомый ток в цепи равняется: . ИЗ доказательства теоремы значит, что величину входного сопротивления можно определить, имея экспериментальные значения , : .

Пример 2. Для схемы (рис.6.3а) определить ток , пользуясь теоремой Нортона.

а) б)

Рисунок 6.5

1. По схеме (рис.6.5б) ток короткого замыкания равняеться:

; ; ; ; .

2. Входное сопротивление пассивного двуполюсника со стороны узлов m, будет представлять:

; ;

3. По схеме (рис.6.5а) находим .

6.3 Энергетические соотношения в цепи постоянного тока

1. Баланс мощностей. Рассмотрим схему, которая состоит из последовательно соединенных реального источника напряжения E и сопротивления нагрузки (рис.3.4а). Согласно со вторым законом Кирхгофа . Умножим это уравнение на I.

. (6.4)

Согласно с определением мгновенной мощности (лекцiя 1), запишем

.

Для постоянного тока выражение (6.4) можно записать:

, (6.5)

где  Мощность энергии, которая производится источником;

 Мощность энергии, которая потребляется в резисторе ;

 Мощность энергии, которая потребляется в ребре .

Итак, выражение (6.5) представляет собой уравнение баланса мощностей: алгебраическая сумма мощностей, которые отдают все источники энергии в цепи, равняется арифметической сумме мощностей, потраченых на сопротивлениях схемы.

Более развернутая форма записи баланса мощностей может быть представлена в таком виде:

, (6.6)

где , ,  количество источников ЭДС, источников тока и резисторов соответственно.

Знак мощности источника зависит от направления тока через источник ЭДС или напряжения на зажимах источника тока. Правило определения знака показано на рис.6.6.

Рисунок 6.6

2. Условие согласования источника с нагрузкой по активной мощности. Условие согласования должно обеспечить максимальную мощность , которая потребляется в нагрузке.

Рассмотрим произвольный линейный двуполюсник. Заменим его по теореме Тевенена эквивалентным источником напряжения (рис.6.4б). Выясним, при котором значении сопротивления нагрузки Мощность , что тратится в нем, будет максимальной: .

Чтобы найти экстремум, решим уравнения :

.

Поскольку знаменатель является положительной величиной и не может равняться нулю, приравняем нулю числитель. Тогда ;

. (6.7)

Формула (6.7) соответствует условию согласования. При этом максимальная Мощность будет представлять:

. (6.8)