5 Основные теоремы теории электрических цепей
Свойства линейных электрических цепей, которые являются общими для цепей любой сложности, сформулированы в теоремах и упрощают задачу анализа цепи.
5.1 Входные и выходные сопротивления и проводимости
В предыдущей лекции были получены формулы для расчета контурных токов и узловых напряжений:
,
; 
,
.
Пусть к какой-то ветке контура электрической
цепи подключен независимый источник
ЭДС
(рис.5.1а), причем эта ветка не является
общей, а принадлежит только контуру m
(независимое это
такой источник, ЭДС которого не зависит
от всех других токов и напряжений
электрической цепи).
а) б)
в) г)
Рисунок 5.1
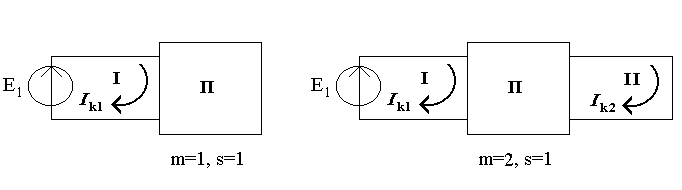
Если другая часть электрической цепи не имеет независимых источников электрической энергии, то по формуле (4.4) предоставленная ЭДС вызовет в данном контуре (m=1, s=1) ток
,
где
входная проводимость,
входное сопротивление.
Итак, входная проводимость m-го контура
(5.1)
это отношение m-го контурного тока к ЭДС, которая действует в этом контуре при отсутствии источников в других контурах. Она показывает, какой именно ток в m-м контуре вызовет единая ЭДС, которая равняется 1 В, которая подключена к этому контуру.
В случае
m =2, s =1 (рис.5.1б) предоставленная
ЭДС
вызовет в контуре 2 ток
,
где
передаточная
проводимость 1-го и 2-го контуров.
Итак, передаточная проводимость m-го и s-го контуров
(5.2)
показывает, какой именно ток вызовет в m-м контуре единая ЭДС, которая равняется 1 В, которая подключена к s-го контуру (индекс m указывает ток, который определяется). Передаточная проводимость также может быть найденна по формуле
; 
.
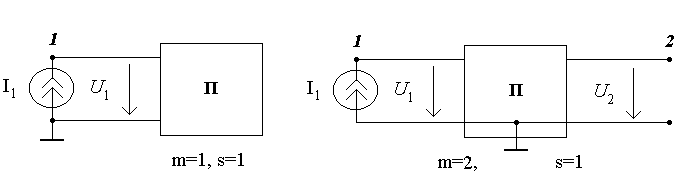
Аналогичные рассуждения касаются также
относительно узлов m и s, если
предположить, что к узлу m подключен
независимый источник тока
,
а другая часть схемы не содержит
независимых источников (рис.5.1в).
Соответственно к (4.8), узловой ток
обусловит появление узловых напряжений
для узла m:
,
где
входное
сопротивление первого узла (m=1, s=1).
Для схемы (рис.5.1г) s=1 узел, к которому включен источник тока, m=2 узел, узловое напряжение которого определяем:
,
где
передаточное
сопротивление первого и второго узлов.
Итак, входное сопротивление m-го узла
(5.3)
показывает, какое именно узловое напряжение узла m вызовет единый источник тока величиной 1 А, которій подключен между m-м и базисным узлами.
Передаточное сопротивление m-го и s-го узлов
(5.4)
показывает, какое именно узловое напряжение вызовет единый источник тока величиной 1 А, которое питает только s-ий узел.
Заметим, что входным сопротивлением
может также называться величина, обратная
к выражению (5.1), а входной проводимостью
величина, обратная
к (5.3). Очевидно, что для одной и
той же пары зажимов электрической
цепи, которая не содержит
источников электрической энергии,
и
является взаимно обратными:
.
5.2 Теорема обратимости (взаемкости)
Пассивные линейные электрические цепи имеют важное свойство, которое известно под названием обратимость. Теорема обратимости, которая базируется на этом свойстве, может быть сформулированна в двух вариантах: относительно источников ЭДС и тока. Ограничимся рассмотрением первого варианта.
Введем такие понятия: внесение источника к электрической цепи носит название возбуждения или влияния; появление тока (напряжения) в цепи носит название реакции или отклика.
На рис.5.2 условно показана
электрическая цепь
с выделенными контурами 1 и 2.
Для первой схемы
;
для второй -
.
Если
,
можно записать
; 
.
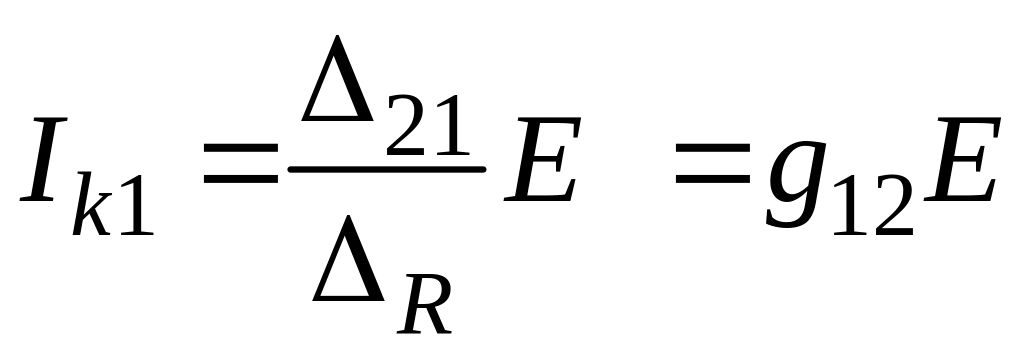Матрица
симметричная,
поэтому
,
,
.
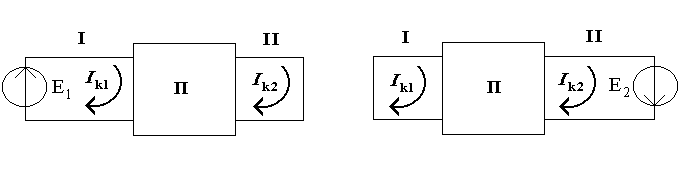
а) б)
Рисунок 5.2
Электрические цепи, для которых
выполняется условие
,
носят название обратных.
Для таких цепей отношение
.
(5.5)
Итак, ЭДС, которая включена в m-м контуреа, вызывает в s-м контуре такой именно ток, который вызовет такая самая ЭДС в m-м контуре, если ее перенести к s-го контура.
Теорема
обратимости может быть сформулирована
иначе: отношение отклика (
) к возбуждению (
) инвариантно (неизменно) к смене мест
отклика и возбуждения.
5.3 Теорема наложения (суперпозиции)
В линейной электрической цепи, которая содержит источник ЭДС, контурные токи (соответственно, токи в ветках) есть линейные функции контурных ЭДС. Согласно с (4.4)
,
где
передаточная
проводимость первого и m-го контуров;
частичный ток, который возникает в
m-м контуре от действия только
источника
,
т.е. при
;
;
при
;
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ;
;
при
.
Итак, ток
в m-м контуре электрической цепи
равняется алгебраической сумме частичных
токов, что вызываются в этом контуре
каждой ЭДС, которая действует отдельно: 
.
Аналогично
для электрической цепи, которая содержит
источник тока, для узловых напряжений
(соответственно, напряжений на элементах
веток) Согласно с формулой (4.8) можно
получить соотношение 
.
Итак, общее формулирование теоремы наложения такое: отклик цепи на несколько возбуждений равняется алгебраической сумме откликов от каждого возбуждения, которое действует отдельно.
Пример. Для схемы (рис.5.3а) по методу наложения найти ток , если известны значения всех элементов.
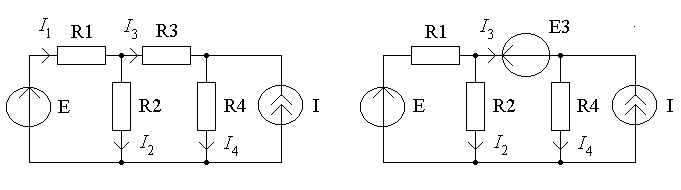
а) б)
Рисунок 5.3
1. Предположим, что
,
.
Исключаем со схемы источник тока
(размыкаем) и находим частичный ток
по методц эквивалентных преобразований,
пользуясь законом Ома и формулой разброса
токов (рис.5.4а).
; 
.
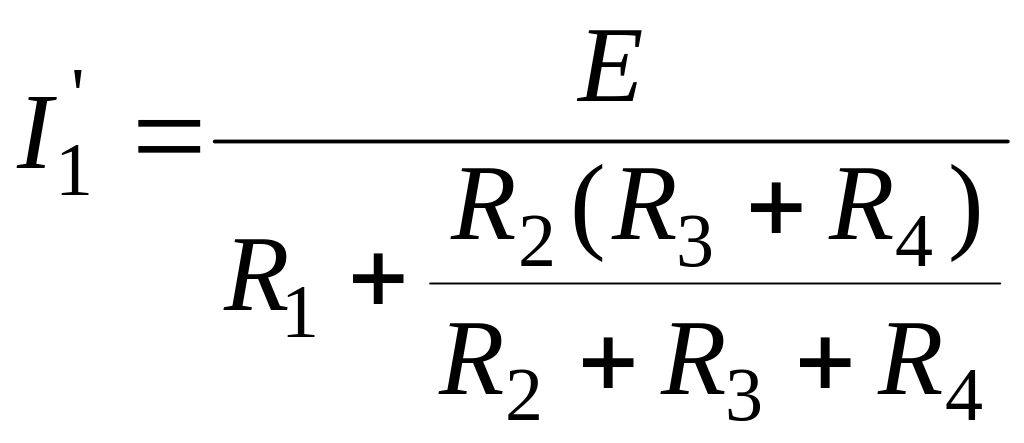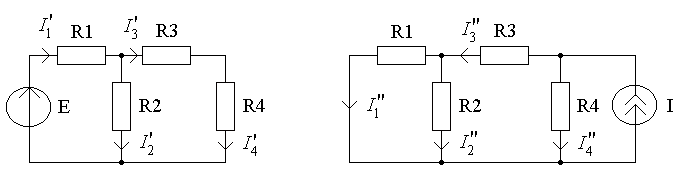
а) б)
Рисунок 5.4