Исходя из формулы (3.6), реальный источник тока приближается к идеальному при условии .

По некоторым соотношениям схемы реальных источников напряжения (рис.3.4а) и тока (рис.3.5а) эквивалентны. Выясним, по каким именно? Соответственно к пpинципу эквивалентних преобразований, напряжение во внешней цепи (т.е., на ребре нагрузка) не может изменяться при переходе от схемы (рис.3.4а) к схеме (рис.3.5a): . Для первой схемы: , для второй: .

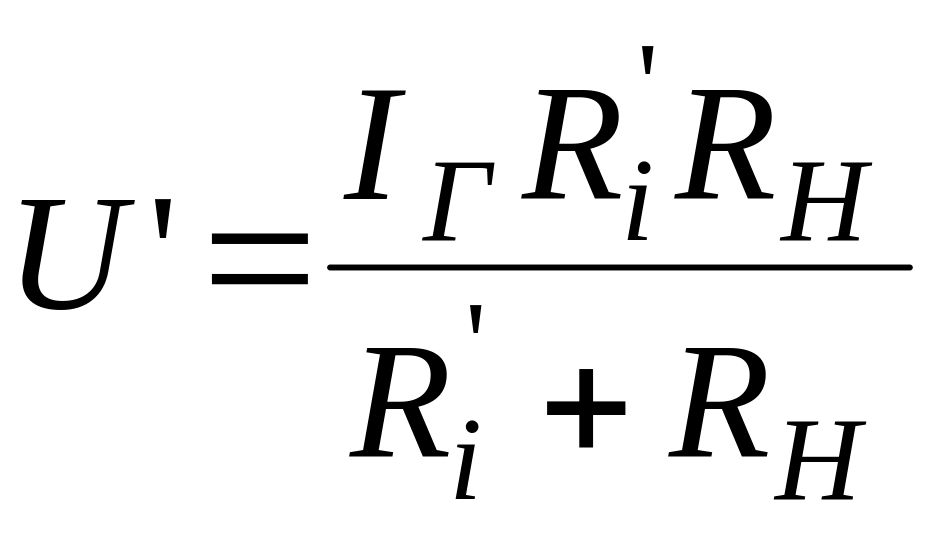Если , то 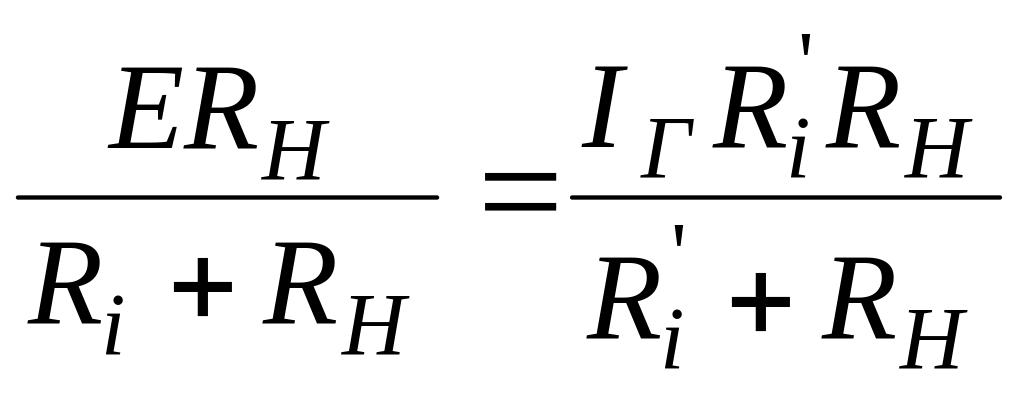, откуда

; . (3.7)

Итак, схемы источников тока и напряжения эквивалентны, если выполняются условия (3.7). Такой же вывод можно получить иначе: схемы источников есть эквивалентними, если их ВАХ совпадают.

Сравнивая ВАХ источника напряжения и ВАХ источника тока (или ), имеем: , . Анализируя (3.7), делаем вывод: внутренние сопротивления источников напряжения и тока при эквивалентном изменении должны равняться друг другу, ток источника при замене схемы (рис. 3.4а) схемой (рис. 3.5а) будет представлять , при обратной замене ЭДС источника напряжения будет равняться .

3. Последовательное соединение n реальных источников (рис.3.6). На основе второго закона Кирхгофа и эквивалентного преобразования последовательно соединенных резисторов будем иметь: ; .

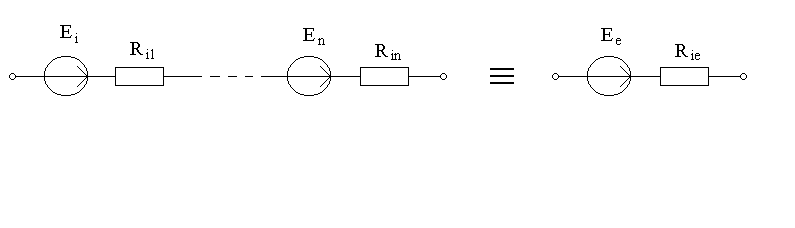
Рисунок 3.6

4. Параллельное соединение реальных источников (pис.3.7). На основе первого закона Кирхгофа подсчитаем (алгебраически) ток источников и заменим параллельно соединенные резисторы эквивалентным резистором . Тогда можно записать

; ; . Если перейти от источника тока к источнику напряжения , тогда ; .

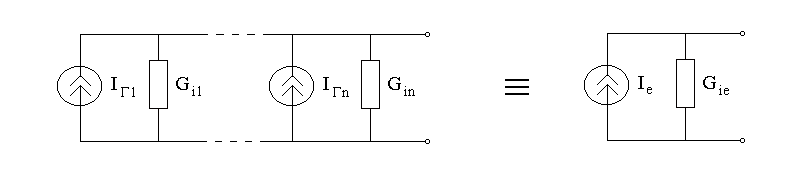
Рисунок 3.7

4 Метод контурных токов и узловых напряжений

Для разветвленных электрических цепей метод уравнений Кирхгофа приводит к необходимости решения большого количества уравнений. Уменьшить количество уравнений позволяют мощные методы Анализа электрических цепей, в частности, методы контурных токов (МКТ) и узловых напряжений (МУН).

4.1 Метод контурных токов

С помощью МКТ анализируют цепи, решая не N (количество веток) уравнений, а (количество независимых контуров) для схем, которые содержат идеальные и реальные источники напряжений (рис.1.1в, рис. 3.4а). При наличии источников с током (рис. 3.5а), последние следует заменить их эквивалентной схемой (рис. 3.4а).

Рассмотрим этот метод на примере схемы (рис.4.1). Пронумеруем узлы и определим количество независимых контуров: = 6-4+1 = 3. Выберем для Анализа как независимые контуры I, II, III. Зададим произвольно направление токов в ветках и направление обхода контуров.

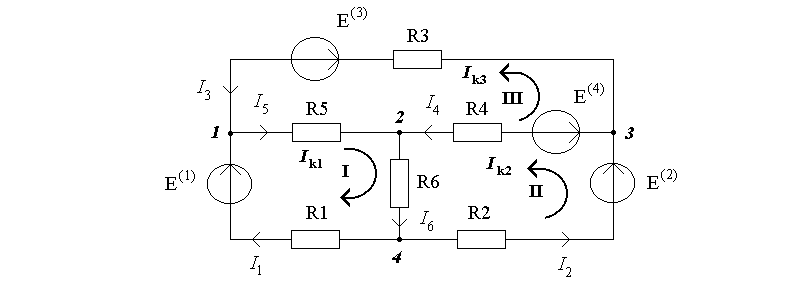
Рисунок 4.1

По второму закону Кирхгофа составим уравнения для первого контура

.

Выразим токи "внутренних" веток , через токи "внешних" веток , , . По первому закону Кирхгофа для узлов 1 и 4 запишем:

; , откуда ; .

Тогда уравнения для первого контура примет вид

.

Сгруппировав слагаемые, будем иметь

. (4.1)

Введем понятие контурных токов, контурных ЭДС и ребер. Контурный ток  ток в главной ветке, номер которой совпадает с номером контура и которая есть внешней ( , , ).

Другими словами, это токи внешних веток, которые условно замыкаются в соответствующих контурах. Для удобства будем считать, что направление контурного тока совпадает с направлением обхода соответственного контура. В общем контурные токи - это условные величины, но в отдельных случаях они могут совпадать с токами веток схемы.

Контурная ЭДС k-го контура  равняется алгебраической сумме всех ЭДС, которые входят в этот контур. Для рассматриваемого примера

; ; .

Собственное сопротивление k-го контура  равняется сумме всех ребер, которые составляют этот контур: ; ; .

Взаимное сопротивление k-го и s-го контуров  равняется сопротивлению ветки, которая входит в эти контуры, со знаком "плюс", если направления контурных токов в ней совпадают, и со знаком "минус", если они противоположны. Для схемы (рис.4.1) имеем ; ; .

С учетом введенных обозначений уравнения (4.1) будет таким:

.

Записав аналогично уравнения для второго и третьего контуров, получаем систему уравнений, из которой можно определить любой контурный ток

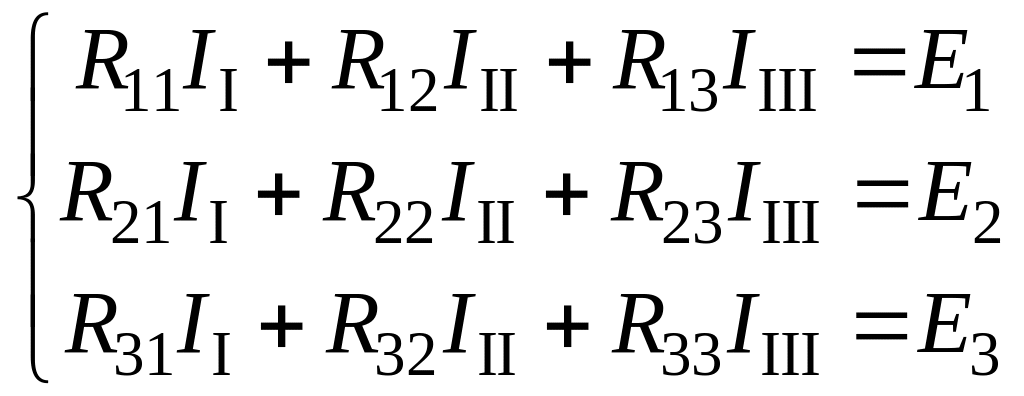, (4.2)

или в матричной форме

, (4.3)

где 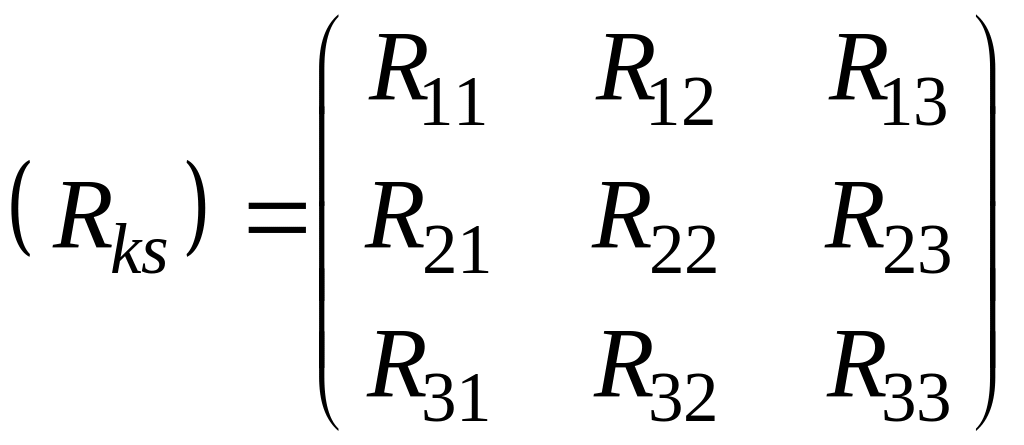 квадратная симметричная матрица сопротивлений, количество строк и столбцов которой равняется n;

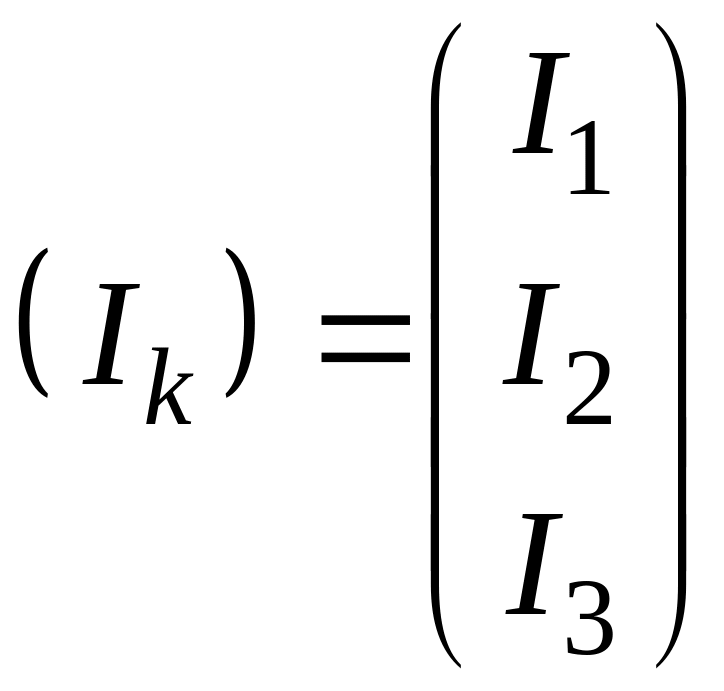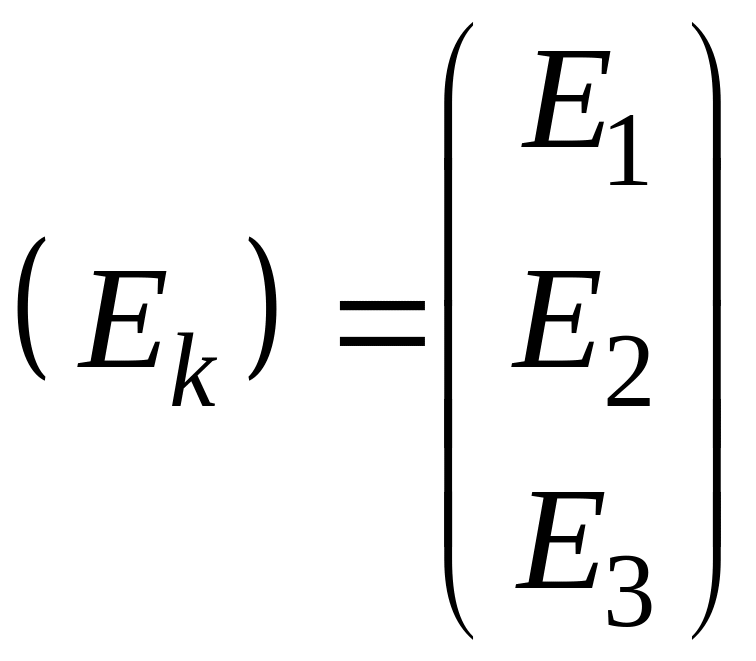;  матрицы контурных токов и ЭДС соответственно.

Итак, МКТ разрешает решить задачу Анализа цепи с количеством уравнений n = NM+1 .Найдем с (4.2) первый контурный ток

,

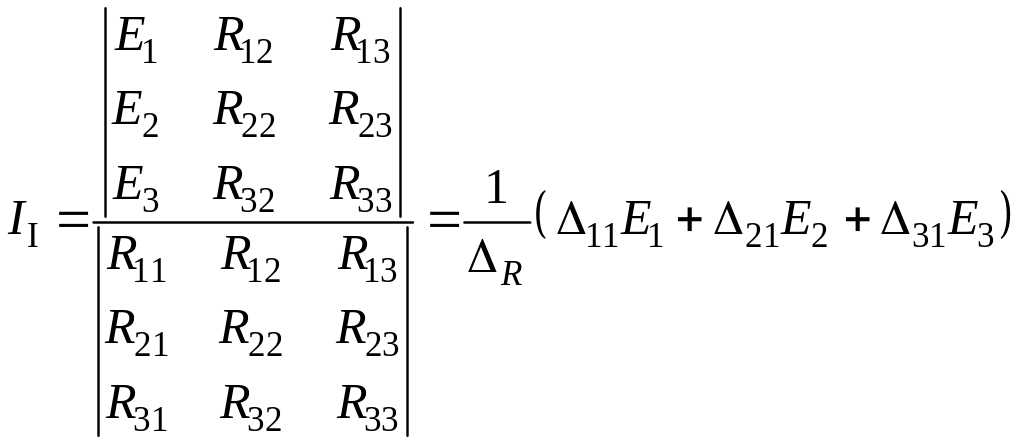где , , ,  определитель и алгебраические дополнение матрицы ребер.

Аналогично можно найти любой (m-и) контурный ток в схеме:

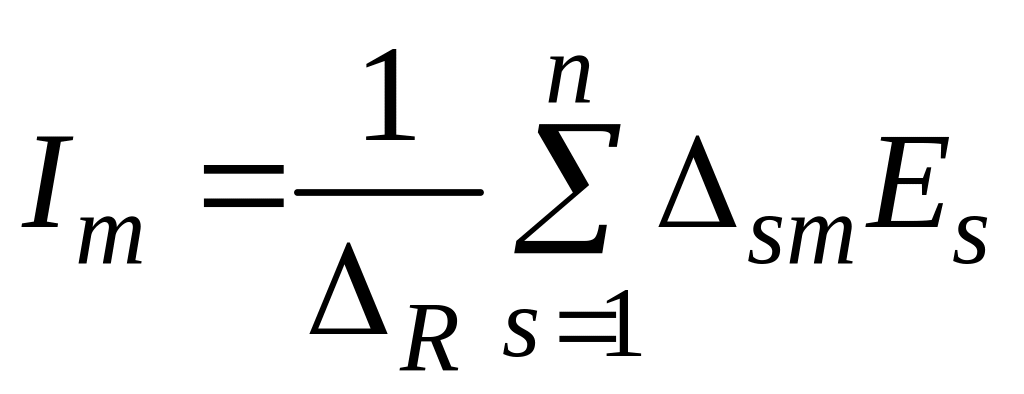, (4.4)

где n = NM+1  количество независимых контуров; m = 1,..., n; s = 1,..., n;

,  определитель и алгебраические дополнение матрицы ребер;

 элемент матрицы-столбца контурных ЭДС.

Токи внутренних веток определяются как линейная комбинация контурных токов. Для схемы (рис.4.1) ; ; .

4.2 Метод узловых потенциалов

Распределение токов и напряжений в электрической цепи не изменится, если один из узлов (любой) заземлить, т.е. сделать его потенциал нулевым.

Базисным носит название узел, потенциал которого равняется нулю. Напряжения других узлов схемы, которые отсчитываются относительно базисного узла, носят название узловых напряжений. Принято узловые напряжения направлять к точке заземления (рис.4.2a). Ток в ветке, которая соединяет узел с базисным узлом, определяется по закону Ома: ; . Напряжение между узлами, ни один из которых не являются базисными, определяется по второму закону Кирхгофа (рис.4.2б): ; .

а) б)

Рисунок 4.2

Анализируя электрический круг по методу МУН необходимо провести эквивалентную замену источников ЭДС источниками тока. Проведем такую замену для электрического цепи (рис.4.1). Обозначим токи источников , а токи в ветках  (рис.4.3).

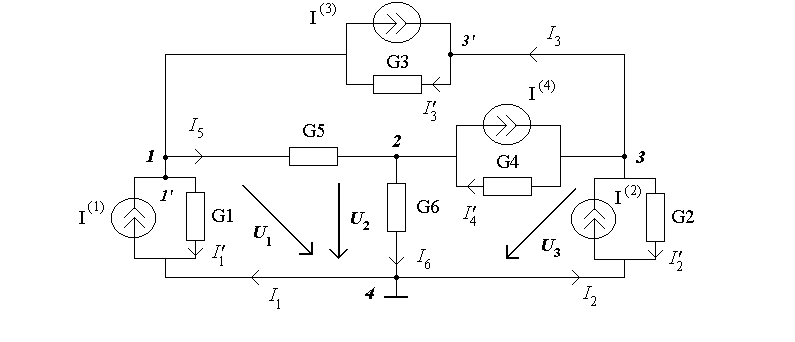
Рисунок 4.3

Изберем как базисный узел 4, и запишем по первому закону Кирхгофа уравнения для узла 1:

, (4.5)

или .

Воспользуемся законом Ома и выразим токи через узловые напряжения:

; ; .

Подставив эти значения к последнему уравнения, будем иметь

;

.

Сгруппировав слагаемые, запишем

. (4.6)

Обозначим  собственная проводимость k-го узла,  которая равняется сумме проводимостей веток, близлежащих к k-му узлу ( , , );

 взаимная проводимость k-го и s-го узлов,  которая равняется сумме проводимостей веток, что соединяют эти узлы, со знаком "минус" ( , ; );

 узловой ток (любого) k-го узла, который равняется алгебраической сумме токов независимых источников, которые сходятся в k-м узле ( , , ). Токи источников, которые втекают в узел (вытекают из узла) входят в узловой ток со знаком «плюс» (со знаком «минус»).

Учитывая эти обозначения, запишем уравнения (4.6) в виде:

.

Записав аналогичные уравнения для узлов 2 и 3, получаем систему:

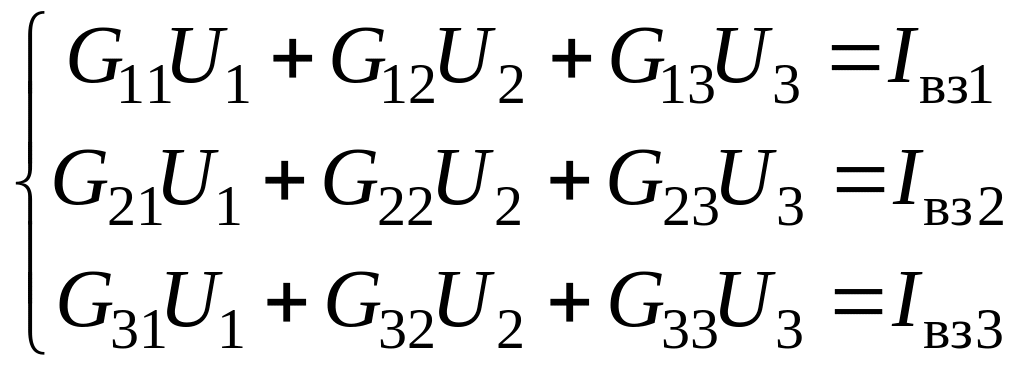. (4.7)

или в матричной форме

,

где 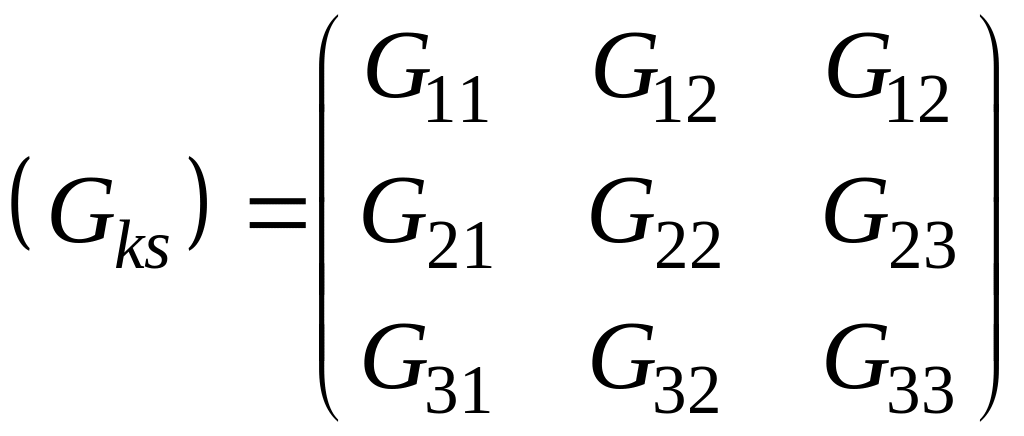, , 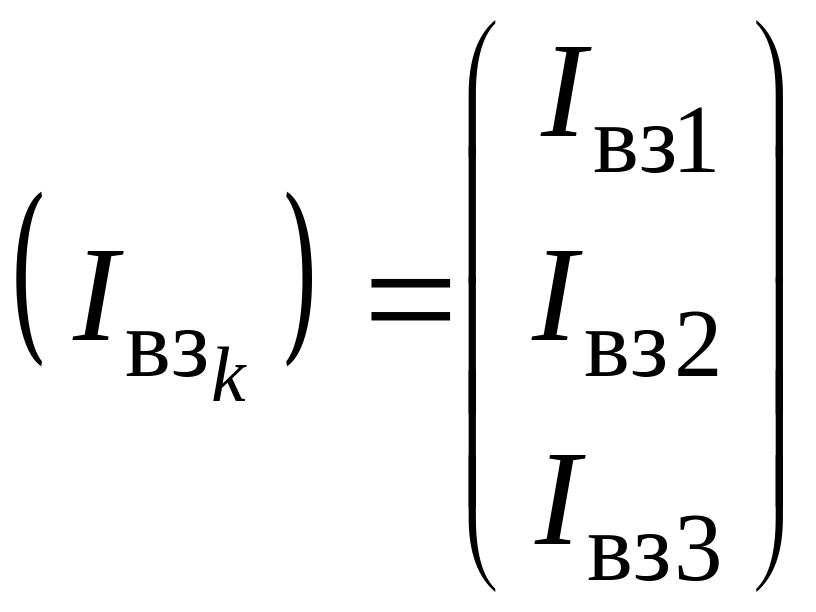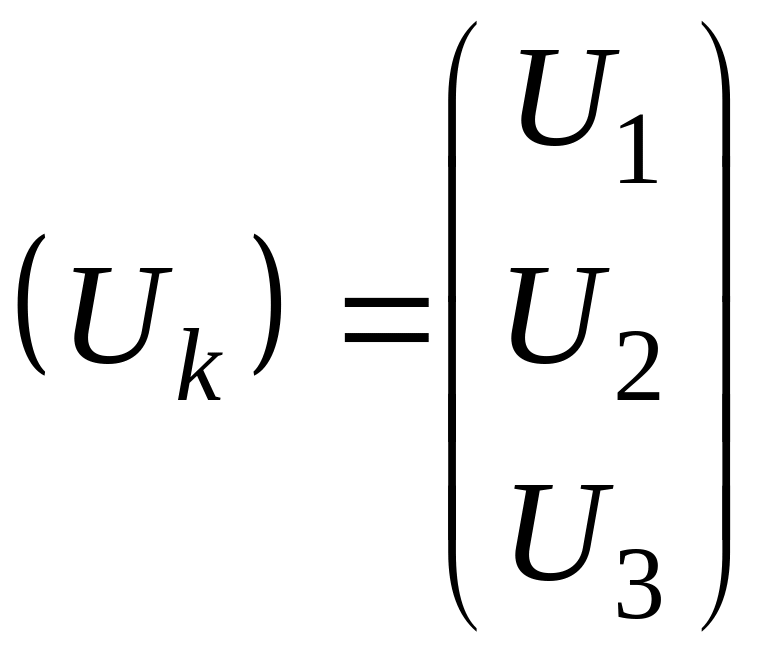 матрицы проводимостей, узловых токов и узловых напряжений, соответственно.

Определим из системы (4.7) узловое напряжение :

.

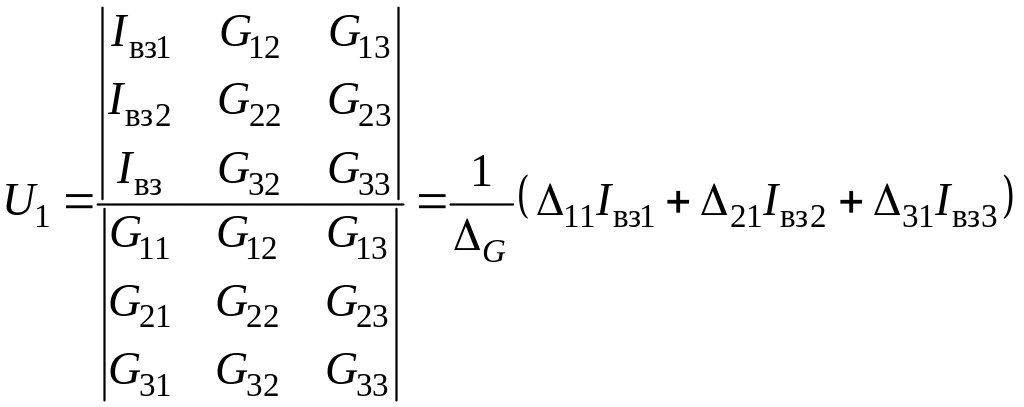Аналогично получаем узловое напряжение любого узла по формуле

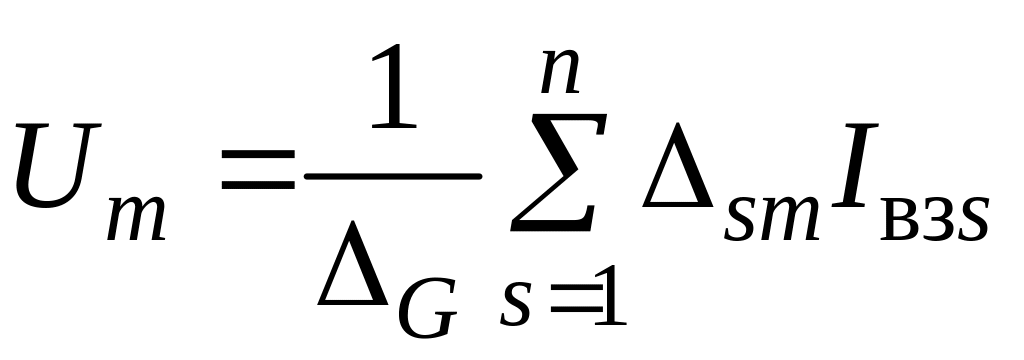, (4.8)

где ,  определитель и алгебраические дополнение матрицы проводимостей [G]; n=M1  количество независимых узлов; m = 1,...,n ; s = 1,..., n.

Напряжения на проводимостях, которые не соединенные с базисным узлом, определяются как линейная комбинация узловых напряжений. Для схемы (рис.4.3)

; ; .

Токи веток определяются по закону Ома: ; ; ; ; ; .

Токи веток выходной схемы (рис.4.1) , определяются по первому закону Кирхгофа с учетом избранных направлений. Например, для узла 1' (рис.4.3) имеем: , откуда ; для узла 3': , откуда , и т.п..

Пример. Для схемы (рис.4.4) по методу МКТ найти ток , если 1 ком; 2 ком; = 1 В; = 4 В, = 2 В.

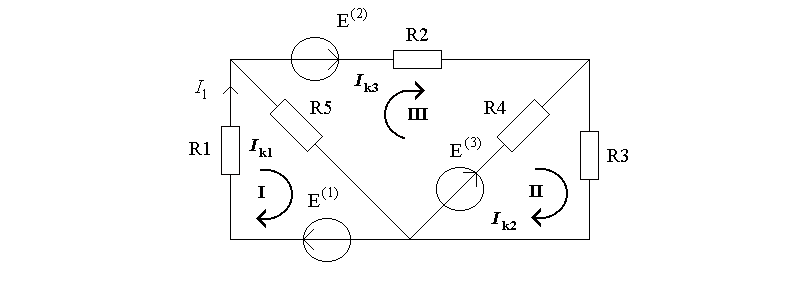
Рисунок 4.4

Обозначив контуры и избрав их обход по часовой стрелке, запишем матрицы (R_ks) и (E_k):

; .

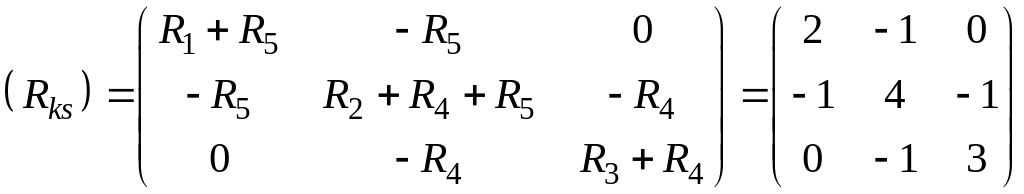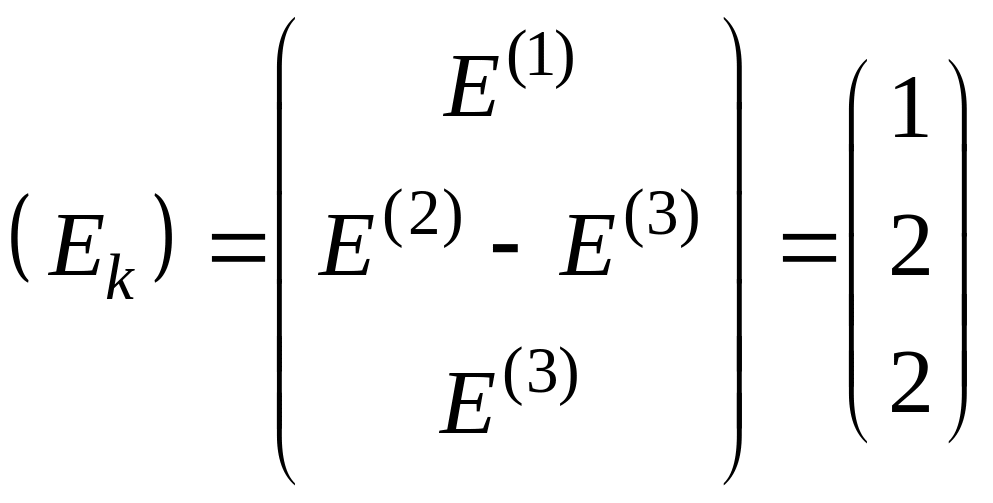По формуле (4.4) определяем первый контурный ток, который будет одновременно и током в ветке .

.
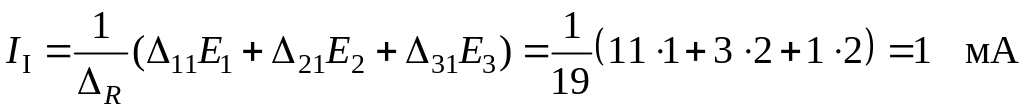