Например, для схемы (рис.2.6) будем иметь

; ; ; .

Эту схему можно подать также как пассивный двухполюсник с входным сопротивлением , к которому подключен источник ЭДС (Е), которое вызывает на внешних зажимах напряжение U. Тогда .

3 Эквивалентное преобразование ребер треугольника в звезду иi наоборот. Эквивалентное преобразование схем с источниками

Рассмотрим схему (рис.3.1а). В данной цепи нет групп ребер, соединенных последовательно или параллельно относительно друг друга.

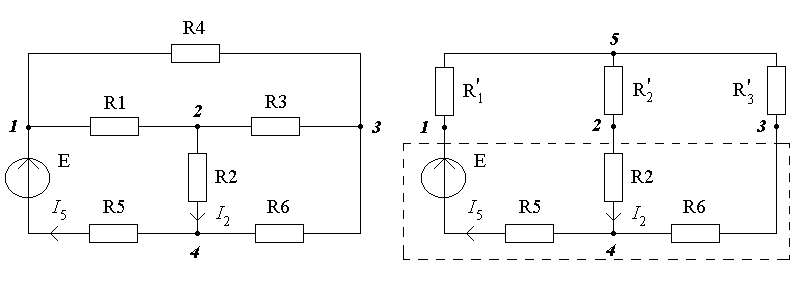
а) б)

Рисунок 3.1

Если цепь с четырьмя и больше узлами не может быть изображена схемой со смешаными соединениями элементов, то она носит название сложноразветвленной цепи. Такие цепи содержат ветки, которые входят в состав так называемых звезд ( , , ; , , ) и треугольников ( , , ; , , ). Такие соединение иногда создают трудности в расчетах элeктрических цепей, и возникает необходимость преобразования треугольника ребер в эквивалентную ЗВЕЗДУ и наоборот для перехода к цепи со смешанным соединением.

3.1 Преобразование треугольника ребер в ЗВЕЗДУ

Пусть известны сопротивления , , , которые образовывают между узлами 1-2-3 треугольник ребер. Определим сопротивления , , , соединенные в эквивалентную ЗВЕЗДУ между теми же самыми узлами (рис.3.2).

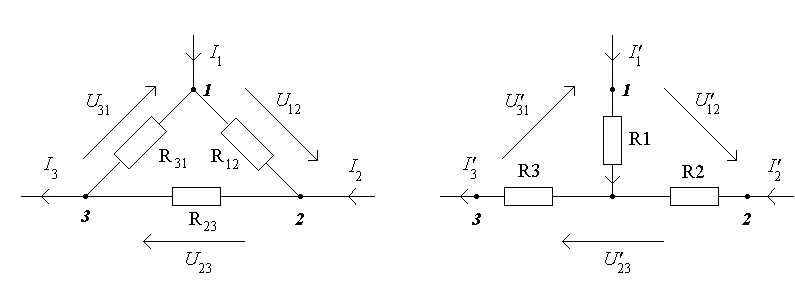Рисунок 3.2

В соответствии с принципом эквивалентных преобразований внешние токи и напряжения не должны изменяться:

; ; ; ; ; .

Чтобы получить формулы перехода от треугольника к звезде, воспользуемся таким приемом. Предположим, что ток . Тогда входное сопротивление со стороны узлов 1-2 для треугольника составит

, а для звезды .

Поскольку , то . Аналогично запишем Входные сопротивления со стороны других узлов. При обозначенных условиях

; ; (3.1)

; ; (3.2)

; . (3.3)

Чтобы определить значение , вычтем из (3.1) уравнение (3.2) и прибавим уравнение (3.3):

;

.

Из последнего уравнения получаем . Проводя замену индексов по цепи 1-2-3-1, можно получить формулы для ребер звезды и :

; ; . (3.4)

Итак, сопротивление луча звезды, соединенного с некоторым узлом, равняется произведению ребер сторон треугольника, соединенных с тем самым узлом, поделенному на сумму ребер всех его сторон.

3.2 Преобразование звезды ребер в треугольник

Для нахождения формул соответствия решим уравнение (3.4) относительно ребер , , . Поделим третье уравнения на первое и второе, а потом подставим к первому.

: ; ;

: ; .

Подставим значение и к первому уравнению, предварительно преобразовав его: .

Тогда будем иметь

;

; .

Формулы для , получают аналогично:

; .

Итак, сопротивление стороны треугольника, близлежащей к двум узлам, равняется сумме ребер лучей звезды, близлежащих к тем самым узлам, плюс произведение этих ребер, разделенных на сопротивление противоположного луча звезды.

Пример. Выполнить расчет токов , в схеме (рис.3.1), пользуясь преобразованием треугольника ребер к звезде. Заменим треугольник ребер между узлами 1-2-3 эквивалентной звездой (рис.3.1б). Часть схемы, обозначенная пунктиром, остается без изменений. Согласно с (3.4) будем иметь

; ; .

Итак, полученная эквивалентная схема (рис.3.1б) имеет только смешанное соединение элементов. В таком случае расчет токов упрощается. Например, ; .

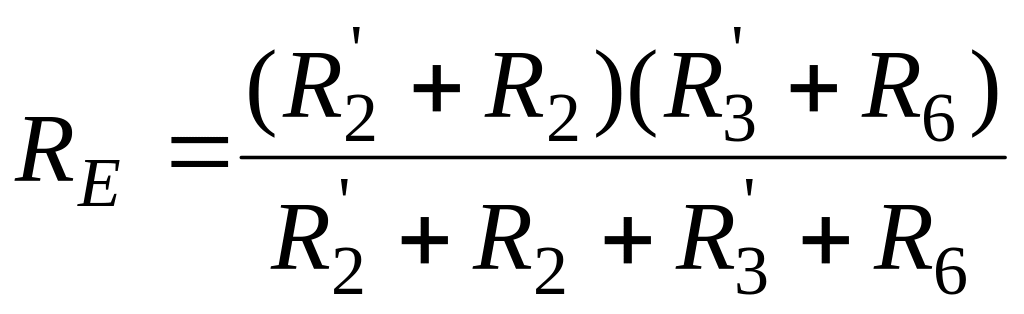Ток можно найти по формуле разброса токов

.

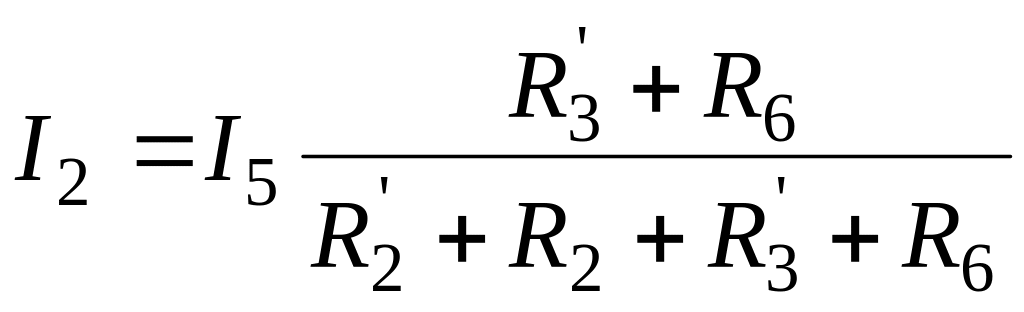3.3 Эквивалентные преобразования схем с источниками

1. Закон Ома для участка цепи с источником.

Рассмотрим понятие одноконтурной (pис.3.3а) и двухузловой схемы (pис.3.3б). Эти схемы характерны тем, что имеют один контур и один независимый узел соответственно.

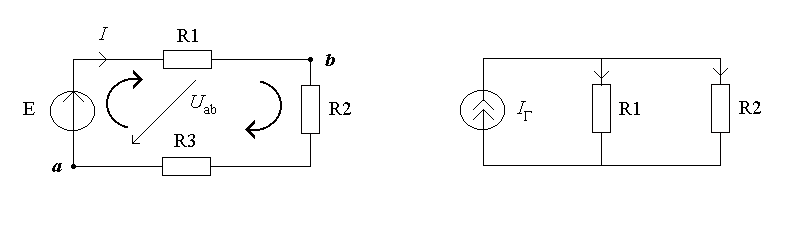
а) б)

Рисунок 3.3

Найдем ток в первой схеме. Согласно второму законом Кирхгофа имеем одно уравнение: , откуда .

Но для данной схемы ток можно найти иначе. Обозначим напряжение между точками a и b: . Тогда для двух условных контуров будем иметь два уравнения:

; .

Из первого получаем закон Ома для участка цепи с источником напряжения:

.

2. Реальные источники электрической энергии и их эквивалентные схемы.

Выше (лекция 1) был определен идеальный источник напряжения, напряжение на зажимах которого не зависит от тока, который в нем проходит и равняется E.

Реальный источник напряжения  активный элемент, который можно подать в виде идеального источника напряжения и последовательно соединенного с ним пассивного элемента , который учитывает потери энергии в источнике (рис. 3.4а).

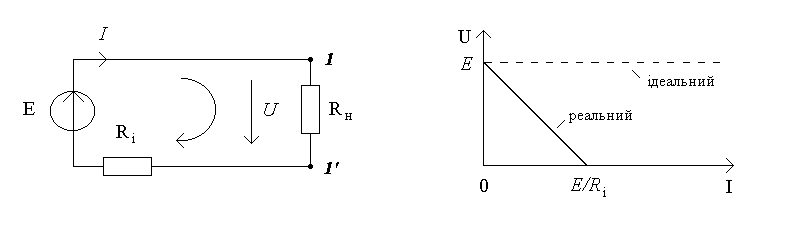
а) б)

Рисунок 3.4

По закону Киpхгофа можно записать , откуда получаем выражение для вольт-амперной харaктeристики реального источника напряжения: (pис.3.4б). Харaктерные точки ВАХ: , ; , . Штриховой линией изображена ВАХ идеального источника напряжения: Е = const.

Выясним, при каких условиях реальный источник приближается к идеальному. Найдем напряжение на зажимах реального источника, к которому подключается сопротивление нагрузки (pис.3.4а):

. (3.5)

Из (3.5) видно, что , если отношение . Итак, чтобы источник напряжения можно было рассматривать как идеальный, необходимо чтобы .

Реальный источник тока  активный двухполюсник, который состоит из идеального источника тока и параллельно соединенного с ним пассивного элемента , который учитывает потери (рис. 3.5а).

Согласно первому закону Кирхгофа можно записать: . Это выражение описывает ВАХ реального источника тока (pис.3.5б). Характерные точки ВАХ такие: , , ; , , . На том же рисунке штриховой линией показано ВАХ идеального источника тока: .

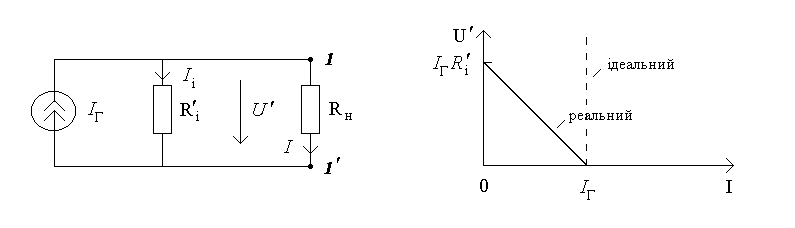
а) б)

Рисунок 3.5

Найдем ток в ребре нагрузки, который подключен к реальному источнику тока (рис.3.5а). По формуле разброса токов

. (3.6)