2 Основные законы и методы расчета
ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
2.1 Элементы топологической структуры цепи
Реальные электрические цепи подаются в виде моделей, в которых все элементы являются идеальными.
Схема ‑ графическая модель электрической цепи, которая изображает ее с помощью идеальных элементов.
Топология схем ‑ раздел, который изучает соединение между собой идеальных элементов, которые входят в электрический круг. Основные элементы топологической структуры цепи (ветка, узел, контур ‑ рассмотрим на примере цепи (рис.2.1а).
а) б)
Рисунок 2.1
Ветка - часть схемы цепи, по которой проходит один и тот же ток. Узел - точка схемы цепи, в которой сходятся не меньше трех веток. Если количество веток равняется двум, узел носит название простого (его можно отстранить).
Контур - запертое очерчивание, которое проходит через узлы и ветки. Количество узлов схемы обозначим M, количество веток - N. Для схемы (рис.2.1а) - M = 4, N = 6.
Граф схемы - графическое представление электрической цепи с сосредоточенными параметрами, в которой ветки изображены отрезками линий – дугами (ребрами), а узлы - точками (вершинами). Граф, который может быть изображен на плоскости без сечения дуг (ребер), носит название планарного графа.
Дерево графа схемы - подграф как совокупность дуг графа, которые совмещают все его вершины, не образовывая контуров. На рис.2.2 показан планарный граф схемы (рис.2.1а) и два из возможных 6-ти деревьев графа.
Хорды графа (главные ветки) - подграф как совокупность дуг графа, которые не входят в выбранное дерево.
Рисунок 2.2
-
количество веток дерева графа;
- количество главных веток дерева.
2.2 Задачи Анализа и синтеза электрических цепей.
Основные законы электрических цепей
Анализ цепи - определение электрического состояния цепи, т.е. определение токов и напряжений в ветках цепи по известным значениям параметров цепи.
Синтез цепи - определение топологии цепи и значений параметров идеальных элементов, из которых составляется круг, которые дают возможность получить заданную характеристику.
Рассмотрим три Основные законы теории электрических цепей.
1. Закон Ома: величина тока в замкнутой
электрической цепи прямо пропорциональна
электродвижущей силе и обратно
пропорциональна сопротивлению
электрической цепи:
.
2. Первый закон Кирхгофа: алгебраическая сумма токов, которые сходятся в узле, в любой момент времени равняется нулю:
.
При этом токи, которые входят в узел, надо брать с одним знаком (например, с "плюсом"), а те, что выходят из узла, - с противоположным ("минусом"). Тогда первый закон Кирхгофа можно сформулировать так: сумма токов, которые сходятся в узле, равняется сумме токов, что выходят из узла. Для каждого из узлов схемы (рис.2.1а) получим такие уравнения:
1.
; 3.
;
2.
; 4.
.
Количество независимых уравнений, которые составляются на основе первого закона Кирхгофа, равняется количеству веток дерева: n=M-1. В данном случае n = 3 (сумма левых частей уравнений для четырех узлов равняется 0, т.е. одно уравнение лишнее).
3. Второй закон Кирхгофа: алгебраическая сумма электродвижущих сил, действующих в запертом контуре электрической схемы, равняется алгебраической сумме спада напряжений на всех участках этого контура в любой момент времени:
,
где n количество ЭДС; m количество пассивных элементов контура
Спады напряжений и ЭДС, направление которых совпадает с направлением обхода контура, берут со знаком "плюс", а все напряжения и ЭДС противоположного направления ‑ со знаком "минус". Значение напряжений записываются в одной части уравнения, а значение ЭДС - в другой. Для схемы (рис.2.1) имеем такие уравнения.
I контур:
;
II
контур:
;
III
контур:
.
Количество независимых уравнений (контуров), которые составляются на основе второго закона Кирхгофа, равняется количеству главных веток дерева и представляет m = N-M+1 = 6-4 + 1 = 3.
Слагаемые рассмотренной системы уравнений определяют из соотношений:
; 
; 
.
Если учесть взаимное соответствие направлений ЭДС и падений напряжений (рис.2.3), второй закон Кирхгофа можно сформулировать так: алгебраическая сумма падений напряжений в запертом контуре равняется нулю.
Рисунок 2.3
2.3 Основные методы расчета электрических цепей
Метод уравнений Кирхгофа. Метод
базируется на решении независимых
уравнений, которые составлены для
заданной цепи по первому и второму
законам Кирхгофа. Предварительно
необходимо определить количество веток
в данной цепи, задать предполагаемые
направления токов во всех ветках и
направления обходов в контурах. Если N
количество веток,
M – количество узлов схемы, то
полученная система уравнений будет
содержать N независимых уравнений: 
.
Решение системы найдем подстановкой напряжений в первую группу уравнений или токов в другую. В обоих случаях получим N токов или напряжений.
Рассмотрим
пример для схемы (рис.2.1а) при E = const,
т.е. рассчитаем режим схемы с постоянным
током; учитывая, что
,
,
получим схему (рис.2.1б):
.
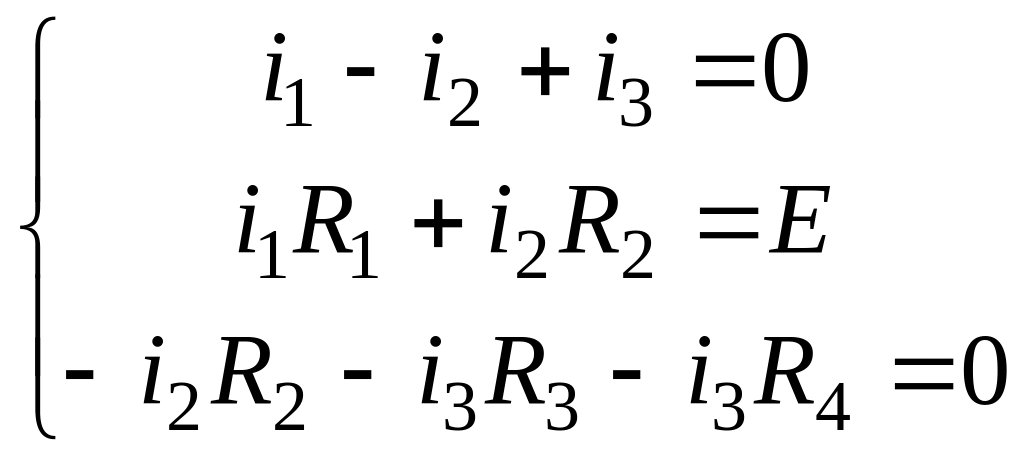Из первого уравнения найдем
и подставим в третье:
;
.
Выразим
и найдем ток
из последнего уравнения:
;
.
Метод эквивалентных преобразований. Преобразования носят название эквивалентных, если при изменении одной части схемы на другую, более простую, токи и напряжения в части схемы, которая не была преобразована, остаются неизменными.
Последовательное соединение элементов цепи соединение нескольких элементов, по которым в них проходит один и тот же ток (рис.2.4).
а)
б)
Рисунок 2.4
В соответствии с принципом эквивалентного
преобразования при переходе от
последовательно соединенных ребер
к эквивалентному сопротивлению
,
внешние токи и напряжения в схемах (рис.
2.4а) не изменяются, т.е.
.
По закону Ома можно записать 
.
Сократив
обе части этого уравнения на i, будем
иметь
.
Рассмотрим Последовательное соединение n индуктивностей (рис. 2.4б). Рассуждая аналогично, будем иметь:
;
.
Сократив на производную токи по времени,
получим:
.
2. Параллельное соединение элементов соединение нескольких элементов так, чтобы все они были под одним и тем же напряжением (рис.2.5а).
а) б)
Рисунок 2.5
В соответствии с принципом эквивалентного
преобразования при переходе от параллельно
соединенных проводимостей
к эквивалентной проводимости
,
внешний ток и напряжение не изменяются,
т.е.
.
Из последнего уравнения по закону Ома можно записать
.
Сократив обе части этого уравнения на u, будем иметь
.
(2.1)
Рассмотрим параллельное соединение емкостей (рис.2.5б). Рассуждая аналогично, будем иметь:
;
.
Сократив
на производную напряжения по времени,
получим:
.
Рассмотрим параллельное соединение
двух сопротивлений. Согласно (2.1) для
участка цепи с R1, R2 (рис.2.6)
.
Поскольку
,
,
,
.
Найдем ток в каждой из параллельных
веток
,
если известен общий ток I и значение
ребер
,
.
По закону Ома
;
.
Тогда 
;
.
Полученное выражение имеет название формулы разброса токов: ток в одной из параллельных веток равняется общему току, умноженному на сопротивление противоположной ветки и поделенному на сумму ребер обеих веток.
3. Смешанное соединение это объединение последовательного и параллельного участков электрической цепи. Различных вариантов соединений может быть много, поэтому общей формулы для определения эквивалентного сопротивления (проводимости) нет. При расчетах таких электрических цепей рассматривают отдельные участки цепи с последовательным и параллельным соединением и применяют соответствующие формулы.
Рисунок 2.6