15 Индуктивно-связанные цепи при синусоидном действии
Предположим,
что к системе двух индуктивно-связанных
катушек подводиться синусоидная ЭДС.
Тогда в каждой из катушек будут протекать
токи:
, 
.
Согласно формуле (14.5) мгновенное значение напряжения на зажимах первой катушки будет иметь вид:
.
Переходя к комплексно-временным функциям, будем иметь
.
Учитывая комутативность операции взятия мнимой части, получаем
;
; 
,
где
комплексное
сопротивление катушки
;
комплексное сопротивление связи;
сопротивление
связи.
С учетом введенных определений коэффициент связи определяется по формуле:
.
Рассмотрим
последовательное соединение двух
индуктивно-связанных катушек, к которым
подводиться синусоидное напряжение
:
1. Согласованное включение (рис.15.1).
Рисунок 15.1
Запишем уравнения по второму закону Кирхгофа для мгновенных значений напряжений:
;
.
Перейдем к комплексной форме записи:
.(15.1)
Векторная диаграмма, построенная по уравнениям (15.1), изображена на рис.15.2а. Уравнения (15.1) можно переписать в таком виде:
,
где
.
Поскольку
эквивалентная индуктивность имеет вид
,
делаем вывод, чтосогласованное соединение
позволяет увеличить общую индуктивность
цепи.
Рисунок 15.2
2. Встречное включение (рис.15.3).
Рисунок 15.3
Рассуждая аналогично, находим:
;
.
Перейдем к комплексной форме записи:
. (15.2)
Векторная диаграмма, построенная по уравнениям (15.2), изображена на рис.15.2б. Уравнения (15.2) можно переписать в таком виде:
,
где
.
Поскольку эквивалентная индуктивность
имеет вид
,
делаем вывод, что встречное соединение
позволяет уменьшить общую индуктивность
цепи.
Как видим, индуктивность взаимосвязанных катушек зависит от коэффициента связи. На этом принципе построены приборы, предназначенные для постепенной смены индуктивности, которые называются вариометрами. Вариометр позволяет изменять индуктивность за счет разного включения двух катушек.
Явление взаимоиндукции широко применяется в технике, на нем основана работа трансформаторов, индукционных катушек в системе зажигания автомашин и т.п..
15.1 Трансформатор
Трансформатор - это устройство для преобразования параметров (амплитуд и фаз) напряжений и токов; он также используется для согласования источника и приемника электрической энергии (нагрузки).
Обмотка - совокупность витков или катушек, которые выполняют определенную функцию в электротехническом устройстве, в частности в трансформаторе.
Обмотка трансформатора, к которой подключен источник, называется первичной; обмотка, к которой подключена нагрузка, называется вторичной.
Рассмотрим трансформатор без феромагнитного сердечника (рис.15.4).
Рисунок 15.4
Указанное на схеме направление токов соответствует встречному включению. Итак, из-за отсутствия источника во вторичной обмотке, катушки подключены встречно. Тогда уравнения по второму закону Кирхгофа для первичного и вторичного контуров можно записать в таком виде:
,
(15.3)
или для комплексных амплитуд
.
(15.4)
По
уравнению (15.4) можно получить эквивалентную
схему трансформатора. Для этого прибавим
и вычтем слагаемое
в первом уравнении и слагаемое
во втором:
,
или сгруппировав слагаемые, перепишем:
.
(15.5)
Как видим, система (15.5) содержит уравнения,
которые составлены по второму закону
Кирхгофа для схемы (рис. 15.5), причем
разница токов
устанавливается соответственно первому
закону Кирхгофа.
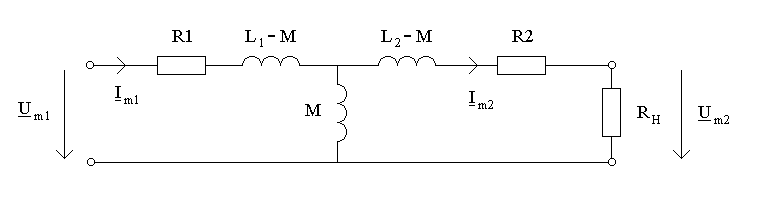
Рисунок 15.5
Итак, полученная схема (рис.15.5) эквивалентна схеме (рис.15.4). Это позволяет сделать вывод: электрические цепи с индуктивно-связанными катушками можно заменить эквивалентними цепями с электрически “связанными” элементами. Такой метод преобразования схем называется развязкой индуктивных цепей.
15.2 Идеальный трансформатор
Идеальный трансформатор характеризуется
тем, что у него отсутствуют потери (
) и магнитные потоки рассеивания. Анализ
свойств идеального трансформатора
позволяет получить некоторые рассчетные
соотношения, которые приблизительно
выполняются также для реальных
трансформаторов.
Смена напряжений и токов в трансформаторе характеризуется коэффициентами трансформации по напряжению и току:
; 
.
В идеальном трансформаторе мощность
первичной и вторичной обмоток одинаковы:
,
или
.
Тогда
.
Определим
коэффициент трансформации идеального
трансформатора в режиме короткого
замыкания. В этом режиме
,
.
Тогда из второго уравнения системы
(15.4) найдем:
,
откуда
.
Эта равенства выполняются также для
модулей комплексных амплитуд и комплексных
действующих значений:
.
В идеальном трансформаторе коэффициент связи k приближается к единице:
,
звiдцепейя
.
С учетом последнего выражения коэффициент трансформации будет представлен:
.
Известно,
что величина индуктивности пропорциональна
квадрату количеству витков обмотки:
;
.
Тогда
.
Если n > 1, трансформатор называется
понижающим, если n < 1
повышающим.
В соответственности с изменением напряжений и токов в трансформаторе наблюдается также трансформация сопротивлений:
,
где сопротивление нагрузки.
Итак, входное сопротивление трансформатора
может отличаться от сопротивления
нагрузки в
раз, что используют для согласования
по мощности.
ПЕРЕЧЕНЬ ССЫЛОК
1. Попов В.П. Основы теории цепей: Учебник для вузов по спец. "Радиотехника". Г.: Высш. школа, 1985. ( 496с.
2. Белецкий А.Ф. Теория линейних электрических цепей: Учебник для вузов. ( М.: Радио и связь, 1986. ( 544с.
3. Агасьян М.В., Мартиненко О.Г. Основы електрорадiотехнiчних цепей: Подручник. ( К.: Высшая шк., 1993. ( 486с.
4. Теоретические основы электротехники. В 3-х ч. Ч.I. Атабеков Г.И. Линейные электрические цепы: Учебник для вузов. ( М.: Энергия, 1978. ( 592с.
5. Зернов Н.В., Карпов В.Г. Теория радиотехнических цепей. ( Л.: Энергия, 1972. ( 816с.
6. Шебес М.Р., Каблучная М.В. Задачник по теории линейних электрических цепей: Учеб. помоги для электротехнич., радиотехнич. спец. вузов. ( М.: Высш. шк., 1990. ( 544с.