2. Влияние сопротивления нагрузки (рис.12.7б).

Преобразуем параллельное соединение элементов C и (B и G) в последовательное по формулам (10.1): ; .

С учетом соотношений , , будем иметь

.

На частоте, близькой к резонансной, получим:

.

Если , тогда , или и единицей в знаменателе можно пренебречь:

; . (12.10)

Зная параметры последовательной эквивалентной схемы (рис.12.8в), , , получаем

;

. (12.11)

Чем меньше сопротивление , тем меньше эквивалентная добротность и тем более широкая полоса пропускания. Итак, для улучшения выборочных свойств цепи необходимо выполнить условие: ; .

13 Параллельный резонансный контур

Параллельный резонансный контур  резонансный контур, который состоит из индуктивного и емкостного элементов, соединенных параллельно (рис.13.1а). Сопротивление растекания конденсатора может быть пересчитано в последовательно соединенное сопротивление (рис.13.1б). Так же, как и для последовательного контура, параметры R, L, C считаются первичными параметрами параллельного контура, причем активное сопротивление равняется сумме ребер катушки и конденсатора при последовательном обходе: .

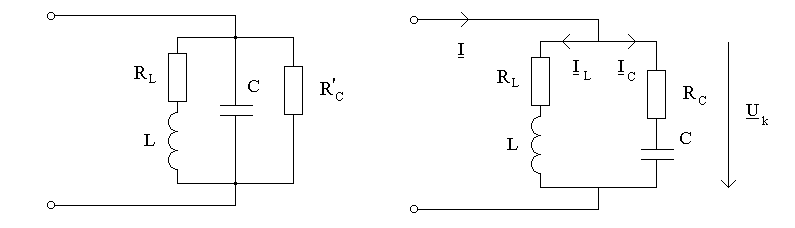
а) б)

Рисунок 13.1

Обозначим сопротивления параллельных веток , и найдем эквивалентное сопротивление параллельного контура

.

Около резонансной частоты , слагаемые и равняются характеристическому сопротивлению . Поскольку для резонансного контура выполняется соотношение , , слагаемыми и в числителе можно пренебречь:

. (13.1)

По определению, резонанс в цепи наблюдается, если сопротивление цепи является чисто активным. Это становится возможным, если .

Найдем вторичные параметры параллельного контура.

1. Резонансная частота: .

2. Характеристическое сопротивление: .

3. Добротность: , .

4. Эквивалентное резонансное сопротивление

; ; .

13.1 Частотные характеристики полного сопротивления параллельного контура

Аналогично последовательному контуру полное сопротивление параллельного резонансного контура определяется как модуль комплексного входного сопротивления, которое обозначено выше . Согласно формуле (13.1)

, (13.2)

где  реактивное сопротивление,  обобщенная расстройка.

Запишем в показательной форме:

, (13.3)

где  модуль , или полное сопротивление контура;

 аргумент ,  фазовая характеристика.

Найдем активную и реактивную составляющие сопротивления :

,

откуда ; . (13.4)

Графики частотных зависимостей, которые построены по (13.3)  (13.4), изображены на рис.13.2. Проанализируем эти графики. Вид кривых , и непосредственно вытекает из аналитической записи.

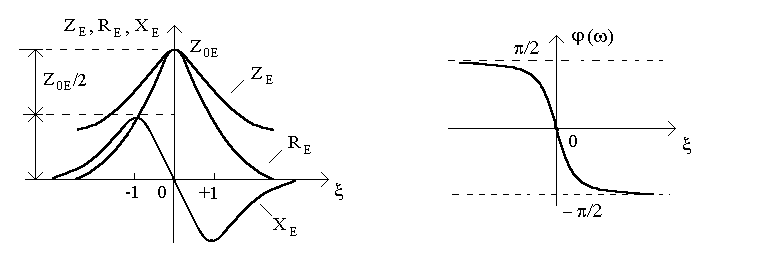
а) б)

Рисунок 13.2

Рассмотрим более подробно график : 1) в области малых расстроек , , т.е. это прямая с отрицательным наклоном; 2) при ; 3) в области больших расстроек , т.е. это гипербола; 4) при , ведь на низких частотах характер реактивности определяет индуктивная ветка; при , ведь на частотах характер реактивности сопротивления определяется емкостью.

13.2 Токи и напряжения в параллельном контуре.

Векторная диаграмма токов

Рассмотрим параллельный контур вида (рис.13.1б). Найдем токи веток , и напряжение на контуре , считая известным ток общей ветки . Расчет сделаем для комплексных действующих значений.

Согласно закону Ома ; ; .

На частоте резонанса выполняются соотношения: ; . Тогда резонансные значения токов и напряжения будут такими: ;

; . (13.5)

Поскольку действующее (амплитудное) значение токов в ветках контура в Q раз превышает действующее (амплитудное) значение тока в общей ветке, резонанс в параллельном контуре носит название резонансном токов.

Итак, резонанс токов - явление резонанса на участке электрической цепи, которая имеет параллельно соединенные индуктивные и емкостные элементы.

Соответственно к найденным выражениям на рис.13.3 приведено векторную диаграмму токов и напряжения в параллельном контуре.

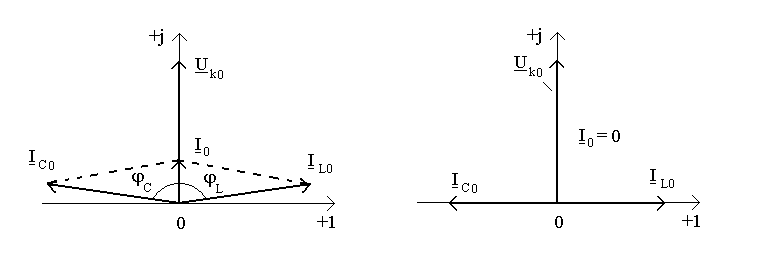а) б)

Рисунок 13.3

Диаграмма (рис.13.3а) изображенная для случая, когда . В таком случае фазовые углы и близки к значению 90, но не равняются ему: ; . Общий ток по величине весьма мал, а по фазе совпадает с напряжением . При резонансе выполняется соотношение . Ток называют током контура.

Векторная диаграмма (рис.13.3б) соответствует идеальному контуру без потерь ( ), который настроен в резонанс. В таком случае токи и точно равняются друг другу и противоположны по фазе: . Поэтому ток в неразветвленном участке цепи равняется нулю. Но при этом в самом контуре циркулирует ток .

13.3 Резонансные кривые параллельного контура

Перейдем от полученных выше частотных характеристик входного сопротивления (13.3) к характеристике напряжения на контуре. Будем считать, что действующее значение тока, который питает контур, неизменно: I = const. Такая ситуация эквивалентна питанию контура генератором тока ( , ). Комплексное действующее значение напряжения на контуре: .

Если I=const, напряжение на контуре зависит от частоты так же, как входное сопротивление (с точностья до постоянного коэффициента). Тогда резонансная кривая напряжения на контуре будет такой:

. (13.6)

Рисунок 13.4

Уравнения резонансных кривых токов находим из выражения (13.5) при условии, что добротность контура достаточно высокая ( , ):

; ; (13.7)

; . (13.8)

Проанализируем полученное выражения и соответствующие графики (рис.13.4):

1) Поскольку кривая является симметричной, а кривая тока получена умножением на проводимость , то максимум смещается в сторону частот, меньших чем резонансная ( );

2) при (рис.13.5,а); при (рис.13.5б).

3) Поскольку кривая получена умножением симметричной кривой на проводимость , то максимум кривой смещается в сторону частот, больших чем резонансная ( ). Граничные значения тока такие: (рис.13.5а); (рис.13.5б).

а) б)

Рисунок 13.5

13.4 Влияние внутреннего сопротивления генератора и сопротивления нагрузки на выборочные свойства параллельного контура

При реальных условиях, когда контур питается реальным генератором, ток I изменяется со сменой напряжения на контуре. Это может существенно повлиять на вид частотных характеристик. В этом случае для исследования выборочных свойств контура следует заменить источник питания эквивалентной схемой с идеальным источником тока (рис.13.6).

Цепь (рис.13.6б) можно рассматривать как некоторый контур, который шунтируется активным сопротивлением и питается в точках 1-1' постоянным током .

Если сопротивление , которое подключено параллельно контуру, пересчитать в последовательное сопротивление по формуле (12.10), добротность эквивалентного контура (по правую сторону точек 1-1') будет представлять

, (13.9)

где .

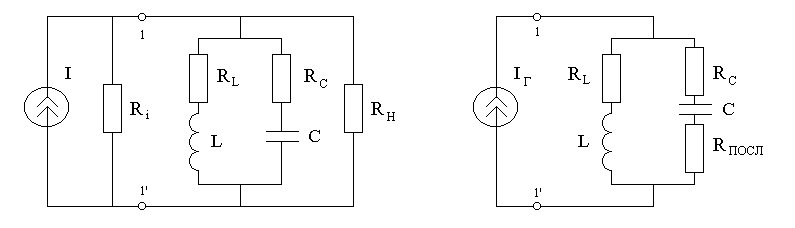
а) б)

Рисунок 13.6

Эквивалентная добротность зависит от собственной добротности и от соотношения сопротивления и внутреннего сопротивления генератора (или сопротивления нагрузки , или и вместе). С уменьшением ( ) эквивалентная добротность уменьшается, т.е. полоса пропускания увеличивается: .

Уравнение резонансной кривой напряжения с учетом влияния ( ) будет иметь вид:

.

Эта характеристика приближается к идеальной резонансной кривой (13.6) лишь при . Если же и контур питается от источника напряжения с ЭДС E, напряжение на контуре вобщем не зависит от частоты, она остается равной значению ЭДС источника E.

Итак, в отличии от последовательного контура, использование параллельного резонансного контура необходимо с точки зрения выборочности тольки в том случае, когда внутреннее сопротивление генератора тока достаточно большое ).