12 Резонансные кривые тока и напряжения последовательного контура

12.1 Резонансная кривая тока. Абсолютная, относительная

и обобщенная расстройка

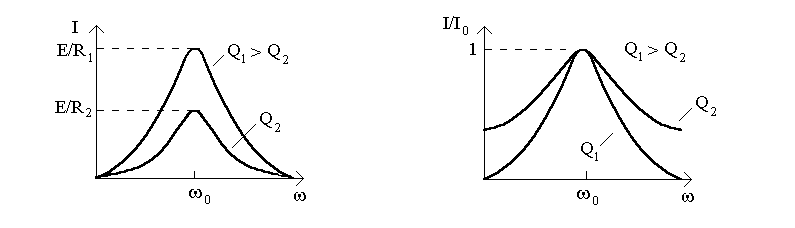
Кривые зависимости модуля комплексного амплитудного (действующего) значения тока или напряжения от частоты генератора называются резонансными кривыми. Уравнение резонансной кривой тока имеет вид:

. (12.1)

Уравнение (12.1) можно записать иначе:

.

Разделив это выражение на резонансное значение тока , будем иметь нормированную резонансную кривую тока:

. (12.2)

На рис.12.1а,б показаны резонансные кривые токов в соответствии с выражениями (12.1) и (12.2) для различных значений добротности .

а) б)

Рисунок 12.1

При расчетах резонансных контуров в радиотехнических устройствах исследуют их поведение главным образом в области частот, близких к резонансной частоте , т.е. когда частота генератора равняется:

; ,

где  абсолютная расстройка, которая является малой величиной по сравнению с резонансной частотой. Расстройка может быть как положительной , так и отрицательной ( , ).

Отношение называется относительной расстройкой. Величина называется обобщенной расстройкой. С учетом введенных обозначений формула (12.2) будет такой:

. (12.3)

Найдем формулы для расчета обобщенной расстройки:

Учитывая, что , получаем точную формулу для вычисления :

.

Но для частот, близких к резонансной частоте контура , выполняются такие приблизительные соотношения: ; .

Тогда

.

Итак, конечная приблизительная формула для нахождения будет иметь вид

.

Резонансная кривая может быть представлена как функция абсолютных, так и функция относительных расстроек (рис.12.2а):

. (12.4)

Если по оси абсциссс откладывать обобщенную расстройку , получим обобщенную частотную характеристику (12.3), которая объединяет все возможные варианты контуров с любой величиной Q (рис.12.2б). Кривая (12.3) не зависит от добротности.

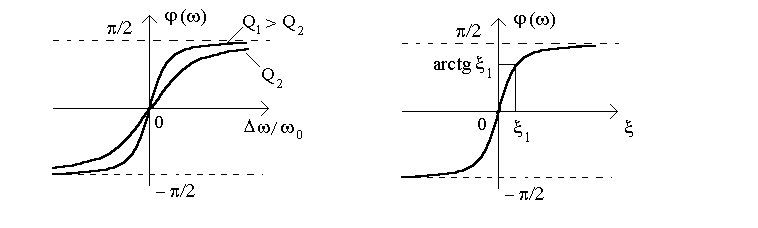
Фазовая характеристика контура также может быть выражена как функция относительной или обобщенной расстройки:

. (12.5)

Фазовые характеристики типа (12.5) изображены на рис.12.3.

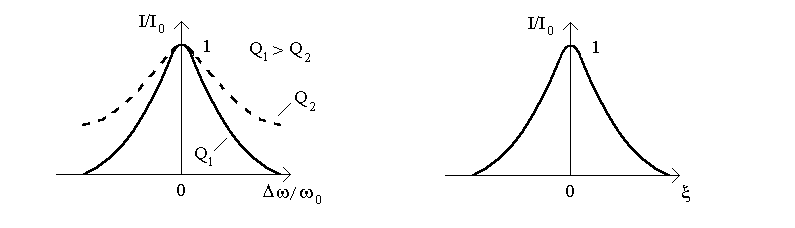
а) б)

Рисунок 12.2

а) б)

Рисунок 12.3

12.2 Резонансные кривые напряжений

Резонансная кривая напряжения  это зависимость модуля комплексного действующего или амплитудного значения напряжения от частоты. Для последовательного резонансного контура согласно закону Ома выполняются такие соотношения для напряжений: ; ; . Подставим сюда значение тока

.

Тогда будем иметь

; ; .

Соответственно, модули полученных выражений являются резонансными кривыми напряжений последовательного резонансного контура:

; (12.6)

; (12.7)

. (12.8)

Анализируя графики, которые построены по этим формулам (рис.12.4), можно сделать такие выводы:

1. Кривая совпадает с резонансной кривой тока с точностью до постоянного множителя. При ; , ; при ; , .

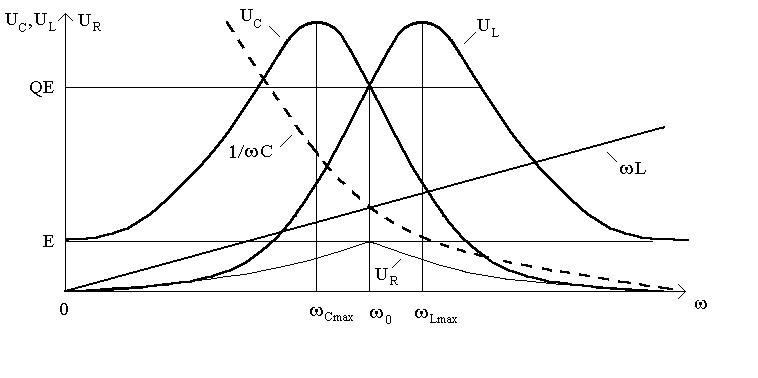
Рисунок 12.4

2. Поскольку кривая I является симметричной, а кривая напряжения получена умножениям кривой тока на емкостное сопротивление , из рисунка видно, что максимум перемещается в сторону частот, меньших по резонансу.

Можно показать, что , где d  затухание.

При напряжение (рис.12.5а). При напряжение (рис.12.5б).

3. Поскольку кривая получена умножением симметричной кривой тока I на индуктивное сопротивление , то максимум перемещается в сторону частот, больших по резонансной частоте . Можно показать, что

.

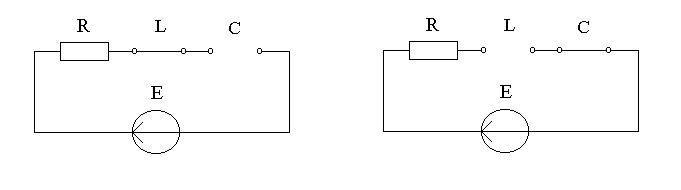
Как видно из рис.12.5, значение напряжения на индуктивности для нулевой и бесконечной частот равняются: ; .

а) б)

Рисунок 12.5

12.3 Виборочность резонансного контура. Полоса пропускания

Выборочность или селективность - это свойство контура из набора колебаний различных частот выделять (пропускать) колебание близкое к резонансной частоте.

То, насколько контур является выборочным, можно оценить по характеру резонансных кривых: чем "острее" резонансная кривая, тем более выборочным является контур. Формула (12.4) показывает, что чем больше добротность Q, тем выше выборочность.

Частотные характеристики резонансного контура по форме значительно отличаются от идеальной П-подобной характеристики. Поэтому частоты, которые пропускаются (выделяются) контуром, определяют условно, вводя понятие полосы пропускания.

Полоса пропускания (П)  это область частот близ резонансной частоты, в пределах которой ток (напряжение) уменьшаются не больше, чем в раз по сравнению с резонансным значением (рис.12.6а). Иначе полоса пропускания - это полоса частот, в пределах которой затухание остается меньшим по определенному значению.

Чтобы определить полосу пропускания, воспользуемся формулой (12.3). По определению полосы пропускания . Т.е.

,

откуда находим два значения обобщенной расстройки, которые соответствуют границам полосы пропускания: (рис.12.6б).

Чтобы определить абсолютное значение полосы пропускания (рис.12.6а), воспользуемся формулой . Учитывая, что , находим связь между полосой пропускания и добротностью:

; .

Для низкодобротных кривых абсолютные расстройки и . Для высокодобротных кривых абсолютные расстройки приблизительно одинаковые, поэтому .

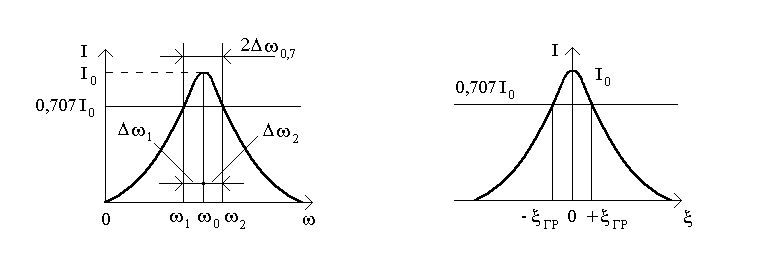
а) б)

Рисунок 12.6

12.4 Влияние сопротивлений источника и нагрузки на выборочные свойства последовательного контура

1. Влияние сопротивления источника (генератора).

Резонансные кривые тока и напряжения в контуре были найдены из таких предположений: ЭДС источника E = const, внутреннее сопротивление . Выясним, как влияет сопротивление реального генератора на свойства контура.

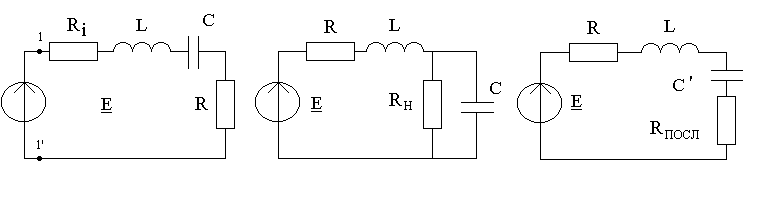
Эквивалентную схему (рис.12.7а) можно рассматривать как резонансный контур, который имеет активное сопротивление и питается в точках 1-1' постоянным напряжением. Для этого контура можно применить все установленные выше соотношения. В частности . (12.9)

Итак, чем больше внутреннее сопротивление , тем меньше эквивалентная добротность цепи и более широкая полоса пропускания. Итак, с увеличением сопротивления выборочность системы ухудшается, т.е. с точки зрения выборочности последовательный резонансный контур следует применять в случае выполнения соотношения .

а) б) в)

Рисунок 12.7