Артоболевский. Теория механизмов и машин. Задачи / Артоболевский. Теория механизмов и машин. Задача 048

48. _{Определить степень подвижности механизма. При наличии звеньев, создающих пассивные связи или лишние степени свободы, их указать и не учитывать при подсчёте степени подвижности механизма. Каждую кинематическую пару четвёртого} класса заменить одним звеном, входящим в две кинематические пары пятого класса. Расчленить механизм на группы Ассура, написать формулу его строения и указать его класс.

Степень подвижности плоского механизма определяется формулой Чебышева:

W=3×n–2×p_н–1×p_в, где

n – количество звеньев механизма;

p_н – количество низших кинематических пар (0–1, 0–3, 0–6, 0–7, 1–2, 2–3, 2–4, 4–5, 5–6, 5–7);

p_в – количество высших кинематических пар.

W=3×7–2×10–1×0=1.

Класс группы Ассура определяется числом кинематических пар, входящих в замкнутый контур.

Порядок группы Ассура определяется числом кинематических пар, которыми группа присоединяется к остальному механизму.

Вид группы Ассура определяется сочетанием видов кинематических пар, входящих в группу.

Расчленение начинается с начального механизма:

Начальный механизм первого класса.

W=3×1–2×1=1.

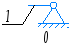
Группа Ассура второго класса, второго порядка, первого вида.

W=3×2–2×3–1×0=0.

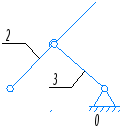
Группа Ассура третьего класса, третьего порядка.

W=3×4–2×6–1×0=0.

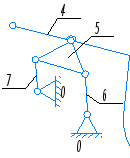
Механизм третьего класса (определяется наивысшим классом групп Ассура).

Формула строения механизма:

.