
Алгоритм решения тз методом потенциалов
1. Построить опорный план.
2. Вычислить потенциалы поставщиков и потребителей и , решив систему уравнений вида .
3. Вычислить оценки
![]() для всех свободных клеток по формуле
для всех свободных клеток по формуле
![]() .
Если
,
то полученный план является оптимальным.
При этом если все
.
Если
,
то полученный план является оптимальным.
При этом если все
![]() ,
то полученный оптимальный план
единственный. В случае если в оптимальном
плане хотя бы одна оценка
,
то полученный оптимальный план
единственный. В случае если в оптимальном
плане хотя бы одна оценка
![]() ,
имеем бесчисленное множество оптимальных
планов с одним и тем же значением целевой
функции. Если же найдется оценка
,
имеем бесчисленное множество оптимальных
планов с одним и тем же значением целевой
функции. Если же найдется оценка
![]() для некоторой клетки
для некоторой клетки
![]() ,
то следует выполнить перераспределение
плана перевозок, загрузив данную
свободную клетку.
,
то следует выполнить перераспределение
плана перевозок, загрузив данную
свободную клетку.
Пример 1.1. В пунктах
![]() производится однородная продукция в
количествах
производится однородная продукция в
количествах
![]() единиц. Готовая продукция поставляется
в пункты
единиц. Готовая продукция поставляется
в пункты
![]() ,
потребности которых составляют
,
потребности которых составляют
![]()
![]() единиц. Стоимость
перевозки единицы продукции из пункта
в пункт
заданы матрицей
единиц. Стоимость
перевозки единицы продукции из пункта
в пункт
заданы матрицей
![]() :
:
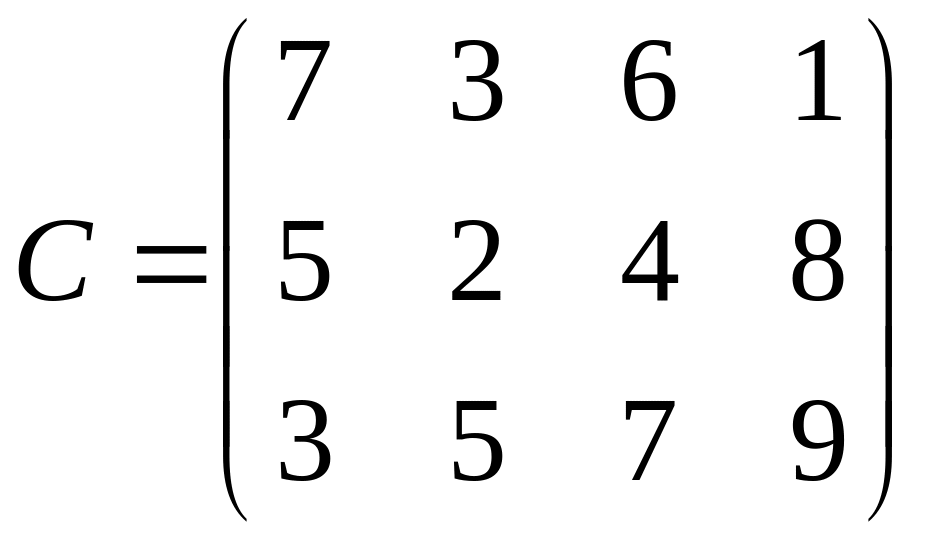 .
.
Требуется:
1) методом потенциалов найти план перевозок продукции, при котором минимизируются суммарные затраты по ее доставке потребителям;
2) вычислить суммарные затраты
![]() .
.
Решение. 1) Определим суммарные запасы продукции и суммарные потребности:
![]() ,
,
![]() .
.
Поскольку
 ,то
есть отсутствует баланс между производимой
продукцией и потребностями, то данная
задача относится к задачам открытого
типа. Вводим фиктивного поставщика
,то
есть отсутствует баланс между производимой
продукцией и потребностями, то данная
задача относится к задачам открытого
типа. Вводим фиктивного поставщика
![]() ,
который имеет запас продукции в объеме
,
который имеет запас продукции в объеме
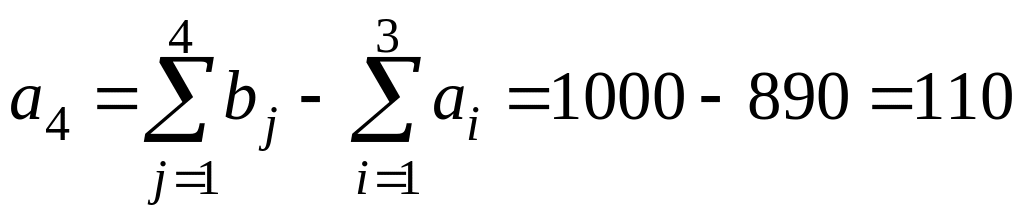 (ед.). Все тарифы на доставку продукции
фиктивного поставщика равны нулю, т.е.
(ед.). Все тарифы на доставку продукции
фиктивного поставщика равны нулю, т.е.
![]() .
Данные задачи занесем в таблицу 1.
.
Данные задачи занесем в таблицу 1.
Таблица 1.
Поставщики |
Потребители |
Запас груза, ai |
|||
B1 |
B2 |
B3 |
B4 |
||
A1 |
7
|
3 160 |
6
|
1 200 |
360 |
A2 |
5
|
2 30 |
4 120 |
8
|
150 |
A3 |
3 160 |
5
|
7 220 |
9
|
380 |
A4 |
0 110 |
0
|
0
|
0
|
110 |
Потребность в грузе, bj |
270 |
190 |
340 |
200 |
1000 |
Начальный опорный план получим по правилу «минимального элемента».
Загрузку начинаем с клетки, которой
соответствует наименьший тариф
![]() всей матрицы тарифов. В нашем случае
минимальным тарифом является
всей матрицы тарифов. В нашем случае
минимальным тарифом является
![]() ,
который соответствует клетке
,
который соответствует клетке
![]() .
В эту клетку вписываем
.
В эту клетку вписываем
![]() .
Исключаем четвертый столбец. У поставщика
.
Исключаем четвертый столбец. У поставщика
![]() осталось еще 160 единиц продукции, которые
поместим в клетку
осталось еще 160 единиц продукции, которые
поместим в клетку
![]() .
Исключаем первую строку. Но потребителю
.
Исключаем первую строку. Но потребителю
![]() необходимо еще 30 ед. продукции, которые
берем у поставщика
необходимо еще 30 ед. продукции, которые
берем у поставщика
![]() ,
и помещаем в клетку
,
и помещаем в клетку
![]() .
Исключаем второй столбец. Оставшиеся
у поставщика
120 ед. продукции помещаем в клетку
.
Исключаем второй столбец. Оставшиеся
у поставщика
120 ед. продукции помещаем в клетку
![]() .
Исключаем вторую строку. Необходимые
потребителю
.
Исключаем вторую строку. Необходимые
потребителю
![]() 220 ед. продукции берем у поставщика
220 ед. продукции берем у поставщика
![]() и помещаем в клетку
и помещаем в клетку
![]() .
Исключаем третий столбец. В пункте
оставшиеся 160 ед. продукции помещаем в
клетку
.
Исключаем третий столбец. В пункте
оставшиеся 160 ед. продукции помещаем в
клетку
![]() .
Исключаем третий столбец. Оставшиеся
110 единиц продукции помещаем в клетку
.
Исключаем третий столбец. Оставшиеся
110 единиц продукции помещаем в клетку
![]() .
.
Полученный нами план является
невырожденным, так как выполняется
условие базисных клеток:
![]() ,
и число заполненных клеток тоже 7. А
значит, получено опорное решение, которое
запишем матрицей
,
и число заполненных клеток тоже 7. А
значит, получено опорное решение, которое
запишем матрицей
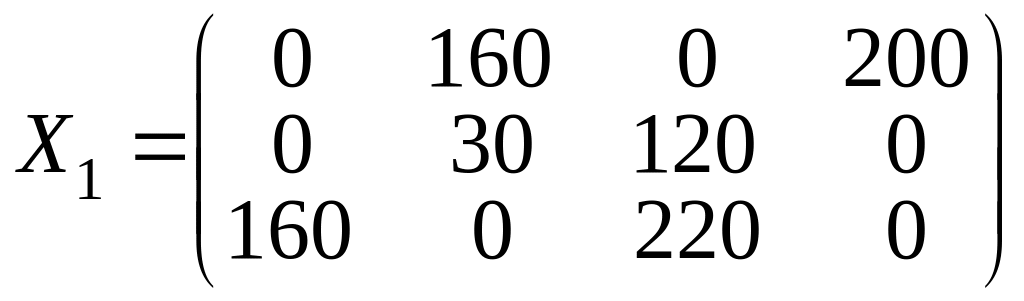 .
.
Методом потенциалов проверим, является ли полученное решение оптимальным. Для этого каждому поставщику и потребителю поставим в соответствие число, называемое потенциалом. Потенциалы выбираем так, чтобы их сумма для каждой загруженной клетки была равна тарифу перевозки единицы груза, т.е.
![]() ,
,
где – потенциал -го поставщика; – потенциал -го потребителя; – тариф заполненной клетки.
В нашем случае получаем следующие уравнения:
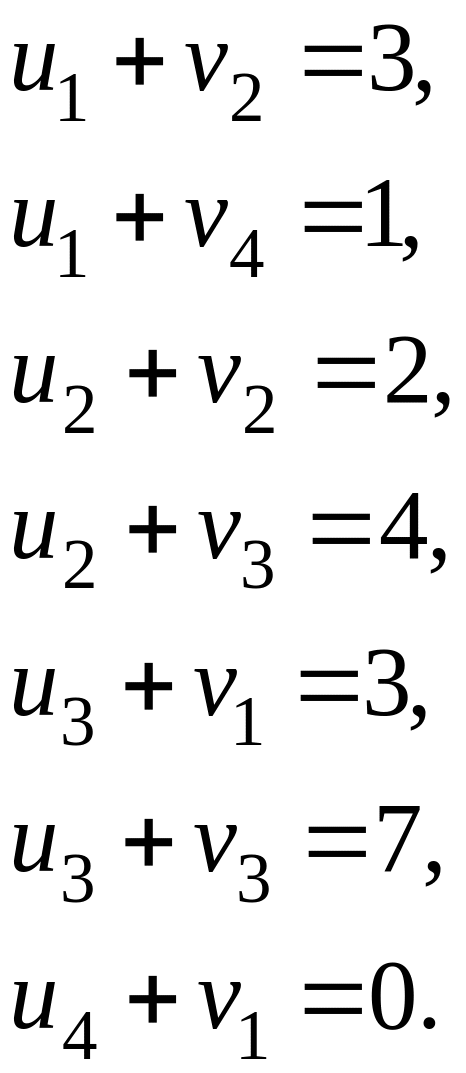
Полагая
![]() ,
получаем следующие значения потенциалов:
,
получаем следующие значения потенциалов:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Все полученные данные заносим в таблицу 2.
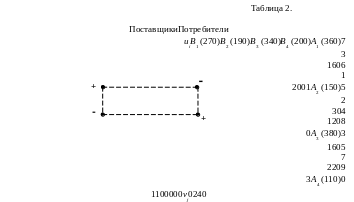
Далее вычисляем оценки свободных клеток по формуле:
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Так как
![]() ,
и
,
и
![]() то полученный план не является оптимальным.
Наиболее потенциальной клеткой является
клетка
то полученный план не является оптимальным.
Наиболее потенциальной клеткой является
клетка
![]() .
Поэтому строим для клетки
замкнутый цикл, который в таблице 2
выделяем пунктирной линией:
.
Поэтому строим для клетки
замкнутый цикл, который в таблице 2
выделяем пунктирной линией:
![]() .
.
Свободной клетке условно приписываем знак «+», тогда следующей клетке по ходу часовой стрелки – знак «» и т.д., знаки чередуются.
В отрицательных вершинах цикла определяем наименьшую загрузку клетки, т.е.
![]() .
.
Количество продукции, равное 110 ед., прибавляем к поставкам в клетках со знаком «+» и вычитаем из поставок в клетках со знаком «».
Получаем новый план, который заносим в таблицу 3.

Проверим, является ли полученный план оптимальным. Для этого каждому поставщику и потребителю поставим в соответствие потенциал. Вычислить потенциалы так же, как это делали выше:
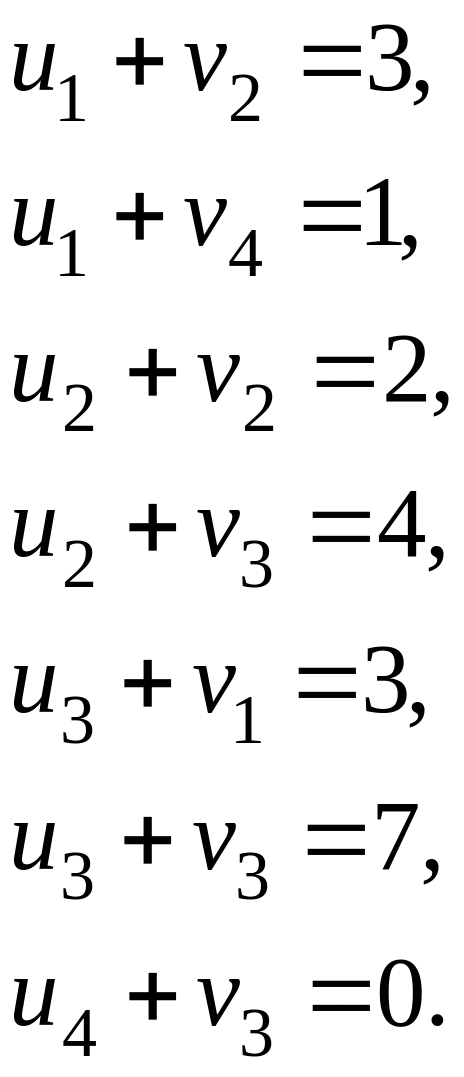
Полагая
![]() ,
получим следующие значения потенциалов:
,
получим следующие значения потенциалов:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
,
,
![]() ,
,
![]() .
.
Вычислим оценки свободных клеток:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Поскольку все , то полученный план является оптимальным, который можно представить в виде матрицы
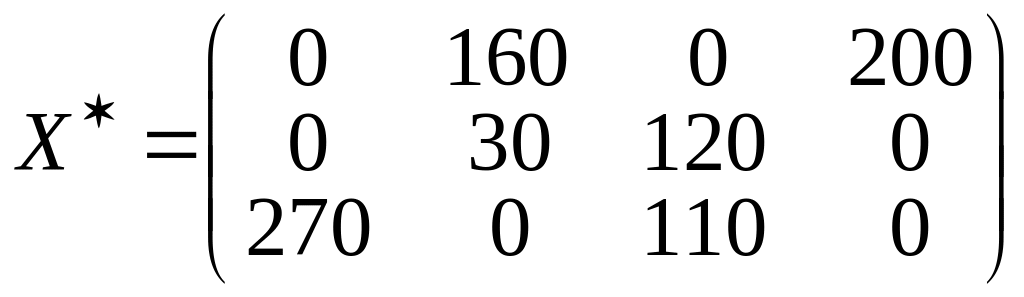 .
.
2) Суммарные затраты при этом будут составлять:

Потребитель B3 не дополучил 110 единиц продукции.
Ответ: оптимальный план перевозок
определяется матрицей
,
суммарные затраты при этом составят
![]()
Пример 1.2. В пунктах
производится однородная продукция в
количествах
![]() единиц. Готовая продукция поставляется
в пункты
,
потребности которых составляют
единиц. Готовая продукция поставляется
в пункты
,
потребности которых составляют
![]()
![]() единиц. Стоимость
перевозки единицы продукции из пункта
в пункт
заданы матрицей
:
единиц. Стоимость
перевозки единицы продукции из пункта
в пункт
заданы матрицей
:
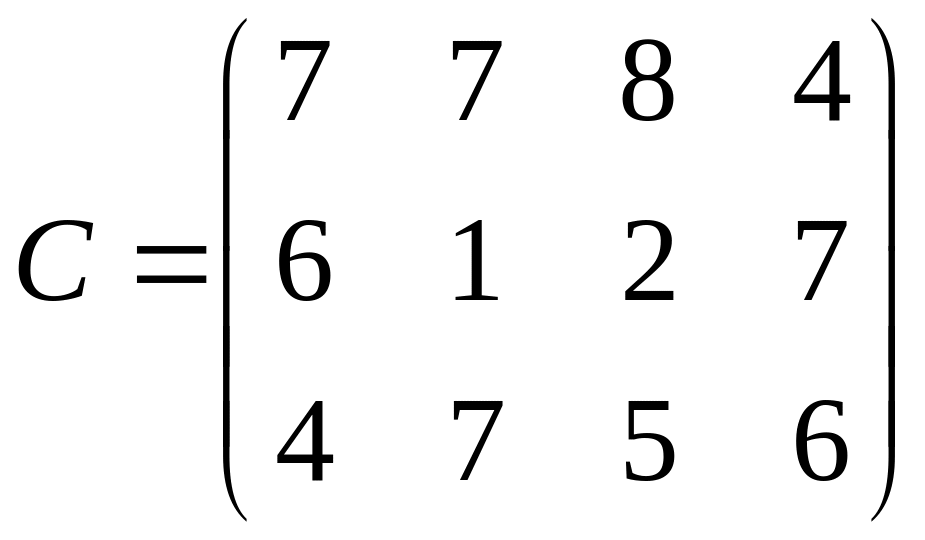 .
.
Требуется:
1) методом потенциалов найти план перевозок продукции, при котором минимизируются суммарные затраты по ее доставке потребителям;
2) вычислить суммарные затраты .
Решение. 1) Определим суммарные запасы продукции и суммарные потребности
![]() ,
,
![]() .
.
Поскольку
 ,то
есть отсутствует баланс между производимой
продукцией и потребностями, то данная
задача относится к задачам открытого
типа. Введем фиктивного потребителя
,то
есть отсутствует баланс между производимой
продукцией и потребностями, то данная
задача относится к задачам открытого
типа. Введем фиктивного потребителя
![]() ,
который нуждается в продукции в количестве
,
который нуждается в продукции в количестве
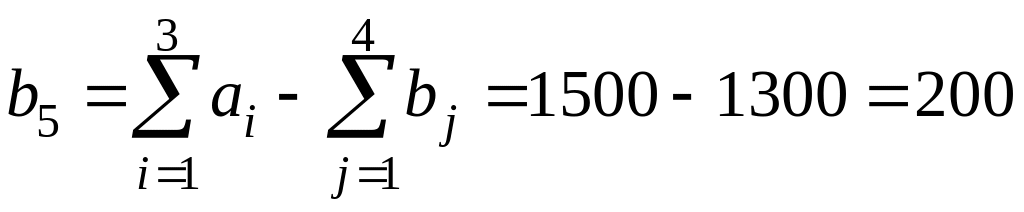 (ед.). Все тарифы на доставку продукции
фиктивному потребителю равны нулю, т.е.
(ед.). Все тарифы на доставку продукции
фиктивному потребителю равны нулю, т.е.
![]()
![]() .
.
Данные задачи занесем в таблицу 1.
Таблица 1.
Поставщики |
Потребители |
ui |
||||
B1 (200) |
B2 (650) |
B3 (150) |
B4 (300) |
B5 (200) |
||
A1 (500) |
7
|
7 |
8
|
4 300 |
0 200 |
0 |
A2 (900) |
6 100 |
1 650 |
2 150 |
7
|
0 0 |
0 |
A3 (100) |
4 100 |
7 |
5
|
6
|
0
|
2 |
vj |
6 |
1 |
2 |
4 |
0 |
|
Начальный опорный план получим по правилу «минимального элемента».
Загрузку начнем с клетки, которой
соответствует наименьший тариф
всей матрицы тарифов. В нашем случае
минимальным тарифом является
![]() ,
который соответствует клетке
.
В эту клетку вписываем
,
который соответствует клетке
.
В эту клетку вписываем
![]() .
Исключаем второй столбец. У поставщика
осталось еще 250 единиц продукции, которые
располагаем следующим образом: 100 единиц
в клетку
.
Исключаем второй столбец. У поставщика
осталось еще 250 единиц продукции, которые
располагаем следующим образом: 100 единиц
в клетку
![]() и 150 единиц в клетку
.
Исключаем вторую строку и третий столбец.
Но потребителю
и 150 единиц в клетку
.
Исключаем вторую строку и третий столбец.
Но потребителю
![]() необходимо еще 100 ед. продукции, которые
берем у поставщика
,
и помещаем в клетку
.
Исключаем первый столбец и третью
строку. 500 единиц продукции у поставщика
размещаем следующим образом: 300 единиц
в клетку
и 200 единиц – в клетку
необходимо еще 100 ед. продукции, которые
берем у поставщика
,
и помещаем в клетку
.
Исключаем первый столбец и третью
строку. 500 единиц продукции у поставщика
размещаем следующим образом: 300 единиц
в клетку
и 200 единиц – в клетку
![]() .
.
Полученный нами план является вырожденным,
так как не выполняется условие базисных
клеток:
![]() ,
а число заполненных клеток равно 6.
,
а число заполненных клеток равно 6.
В одну из базисных клеток, например, в
клетку
![]() таблицы 1 вписываем число нуль
«нуль-загрузку», и эту клетку считаем
базисной.
таблицы 1 вписываем число нуль
«нуль-загрузку», и эту клетку считаем
базисной.
Заметим, что нельзя вписывать 0 в клетки
![]() и
,
поскольку образуется цикл. Если вписывать
0 в другие незанятые клетки, то произойдет
перераспределение продукции, количество
которого равно 0. И в итоге заполниться
клетка
.
и
,
поскольку образуется цикл. Если вписывать
0 в другие незанятые клетки, то произойдет
перераспределение продукции, количество
которого равно 0. И в итоге заполниться
клетка
.
Таким образом будет выполнено условие занятости базисных клеток: . В результате получено опорное решение, которое запишем матрицей
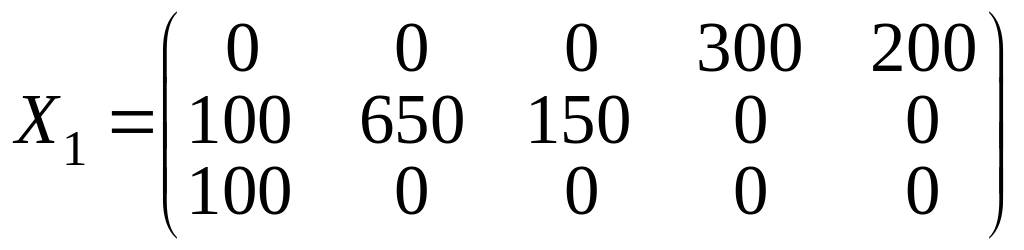 .
.
Методом потенциалов проверим, является ли полученное решение оптимальным. Для этого каждому поставщику и потребителю придается число, называемое потенциалом. Потенциалы выбираем так, чтобы их сумма для каждой загруженной клетки была равна тарифу перевозки единицы груза, т.е.
,
где – потенциал i-го поставщика; – потенциал j-го потребителя; – тариф заполненной клетки.
В нашем случае получаем следующие уравнения:
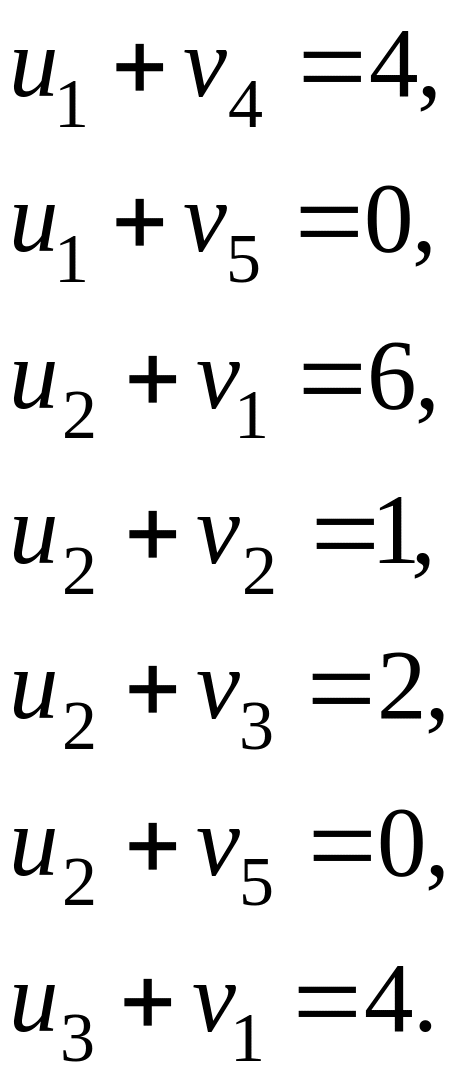
Полагая , получаем следующие значения потенциалов:
![]()
![]()
![]()
![]()
![]()
![]() .
.
![]()
![]()
Все полученные данные заносим в таблицу 1.
Далее вычисляем оценки свободных клеток по формуле:
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Поскольку все , то полученный план является оптимальным и единственным. Представим его в виде матрицы
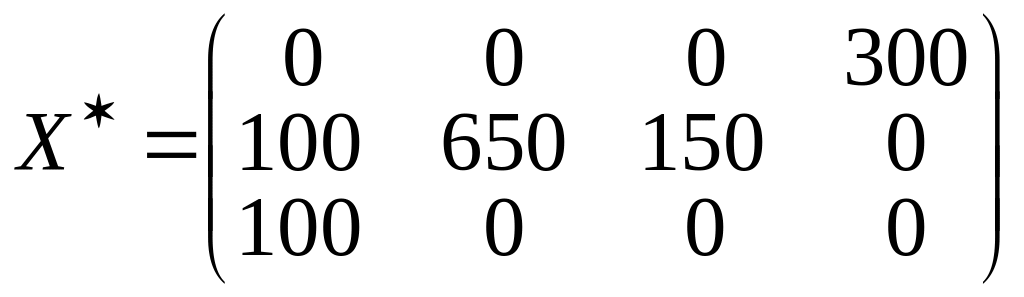 .
.
2) Суммарные затраты при этом будут составлять:
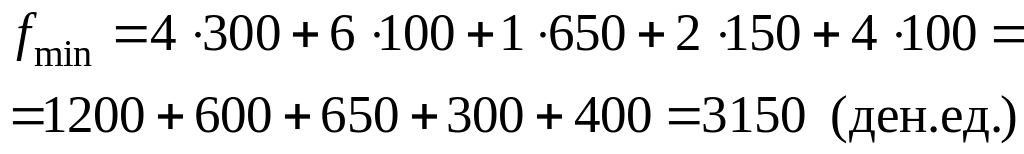
В пункте A1 нераспределенными остались 200 единиц продукции.
Ответ: оптимальный план перевозок определяется матрицей
,
суммарные затраты при этом составят
![]()
