Тема 3. Дифференциальные уравнения порядка выше первого. §1. Простейшие случаи понижения порядка.
Дифференциальное
уравнение порядка
имеет вид:
. (1.1)
В некоторых случаях порядок уравнения может быть понижен, что обычно облегчает его интегрирование.
Случай
1.
Дифференциальное уравнение не содержит
искомой функции и ее производных до
порядка
,
т.е. имеет вид:
. (1.2)
Замена
понижает порядок
.
Пример 1. Проинтегрировать дифференциальное уравнение
. (1.3)
Решение.
Замена:
.
Тогда
и уравнение (1.3) перепишется в виде
.
(1.4)
Уравнение (1.4) – первого порядка. Интегрируем уравнение (1.4). Это уравнение с разделяющимися переменными:
,
,
или
,
откуда
.
Возвращаемся к прежним переменным:
. (1.5)
,
и находим
.
Ищем
потерянные решения. Интегрируя уравнение
(1.5), мы делили на константу
,
т.е. теряли семейство решений:
,
или
,
или
.
Разделяя
переменные при интегрировании в уравнении
(1.4), делили на неизвестную
:
,
т.е.
.
Подставляя в исходное уравнение (1.3),
убеждаемся, что это решение.
В
процессе решения также делили на
выражение
,
т.е.
.
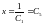Подставляем в уравнение (1.3) и убеждаемся,
что
решением не является.
Итак, все решения уравнения (1.3) – это двухпараметрическое семейство функций и два однопараметрических семейства и .
Случай
2.
Дифференциальное уравнение не содержит
независимой переменной
,
т.е. имеет вид:
. (1.6)
В
этом случае порядок уравнения можно
понизить, взяв
за новую независимую переменную, а за
новую неизвестную функцию:
:
.
Пример 2. Решить уравнение
. (1.7)
Решение. Замена: . По правилу дифференцирования сложной функции находим
.
Уравнение (1.7) принимает вид:
, (1.8)
порядок уравнения понижен. Уравнение (1.8) является уравнением с разделяющимися переменными. Интегрируем данное уравнение
,
,
,
где
.
Отсюда
,
и имеем два уравнения первого порядка:
1) 
,
,
;
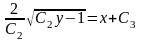2)
,
,
Эти два ответа можно объединить одной формулой:
,
или
,
где
– любое действительное число. Потерянных
решений нет.
Случай 3. Порядок дифференциального уравнения легко понижается, если удается преобразовать его к такому виду, что правая и левая части равенства являются полными производными от каких-либо функций.
Пример 3. Решить уравнение
. (1.9)
Решение. Переписываем уравнение (1.9) в виде
. (1.10)
Замечаем,
что
,
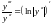а
.
Тогда равенство (1.10) можно записать как
равенство полных производных:
.
Таким образом, функции
и
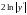отличаются на постоянную, т.е.
. (1.11)
Порядок уравнения понижен.
Потенцируем равенство (1.11):
или
(1.12)
Опять применим тот же прием. Переписываем (1.12) в виде
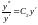
и получаем
.
Откуда
.
Порядок полученного уравнения понижается. Потенцируем:
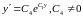(1.13)
Интегрируем уравнение (1.13):
,
отсюда
,
или
,
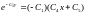или
,
где
–
любое действительное число.
Логарифмируя полученное выражение, получаем
.
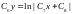Ищем потерянные решения:
. (1.14)
входит
в семейство решений (1.14) при
.
Случай
4.
Дифференциальное уравнение однородно
относительно
,
т.е. если дифференциальное уравнение
имеет вид
,
то существует такое число
,
что справедливо тождество
.
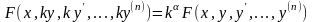В
этом случае говорят, что
– однородная функция порядка
по всем своим аргументам, начиная со
второго.
Порядок
уравнения можно понизить заменой
:
.
Пример 4. Решить уравнение
. (1.15)
Решение. Проверяем, что дифференциальное уравнение (1.15) однородно, переписывая его в виде:
.
Имеем
,
,
где
функция
– однородная порядка
.
Полагаем
,
тогда
, (1.16)
.
Подставляем полученные выражения в (1.15):
,
или
,
или
. (1.17)
Порядок исходного уравнения понизили.
Интегрируем уравнение (1.17)
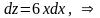
и возвращаемся к прежним переменным:
,
или
где
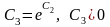– любое действительное число.