Розв’язання задачі двоїстим симплекс-методом

Мета – навчитися будувати двоїсті задачі, розуміти економічну інтерпретацію двоїстих задач та визначати початковий опорний план двоїстим симплекс – методом

Розв’язання. Запишемо двоїсту задачу до заданої. Для цього:

1. Всі нерівності системи обмежень є виду " ≥ "

2. Складемо цільову функцію двоїстої задачі

Число змінних двоїстої задачі дорівнює числу обмежень прямої.

3. Запишемо матрицю А коефіцієнтів при змінних отриманої системи і транспонуємо її

;

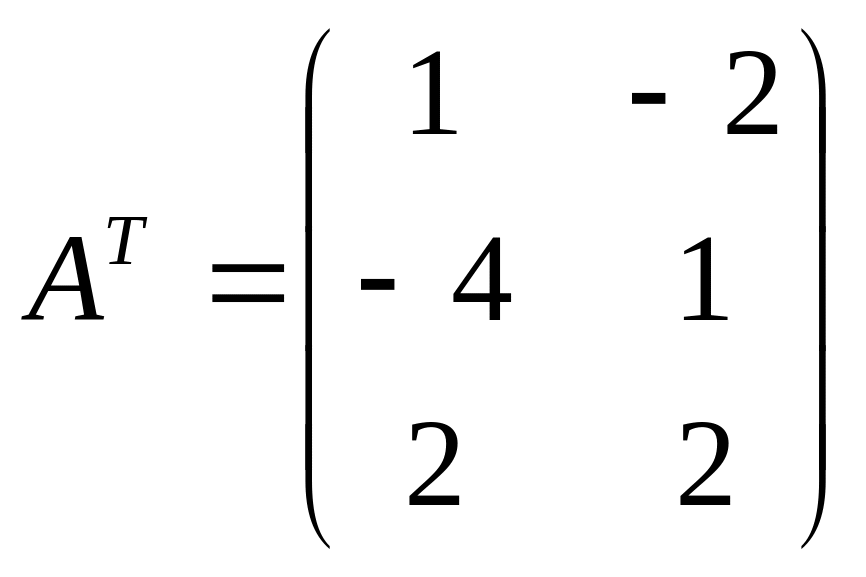
4. Запишемо систему обмежень двоїстої задачі: ; .

Розв’яжемо пряму задачу. Для цього зведемо її до канонічної форми:

при обмеженнях

Запишемо систему обмежень у векторній формі:

де ; ; ; ; ;

Розв’язання задачі будемо здійснювати двоїстим симплекс-методом поетапно.

Етап 1. Знайдемо псевдоплан прямої задачі, зведеної до канонічної форми. Помножимо перше і друге рівняння системи обмежень на (─1) і отримаємо таку задачу:

при обмеженнях

Вектор є розв’язком системи лінійних рівнянь, але цей розв’язок не може бути оптимальним планом задачі, оскільки серед його компонент є від’ємні числа. Такий розв’язок (план) називається псевдопланом задачі.

Етап 2. Складаємо симплекс-таблицю (табл. 7)

Таблиця 9

i	Базис		A0	C1=-8	C2=-8	C3=-20	C4=0	C5=0
				A1	A2	A3	A4	A5
1	A4	0	-2	-1	4	-2	1	0
2	A5	0	-1	2	-1	-2	0	1
m+1			0	8	8	20	0	0

З табл.9 бачимо, що планом двоїстої задачі є вектор Y(0,0) Компоненти оптимального плану двоїстої задачі збігаються з відповідними числами рядка симплекс-таблиці розв’язку прямої задачі. Ці числа стоять у стовпцях векторів, які відповідають додатковим змінним. Значення цільової функції на цьому плані

Оскільки в рядку від’ємних чисел немає, а серед чисел стовпця вектора A₀ є два від’ємних числа (─2 і ─1), то згідно з двоїстим симплекс-методом можна перейти до повної симплекс-таблиці. В нашому прикладі це можна зробити, оскільки в рядках векторів A₄ і A₅ є від’ємні числа. Якщо в цих рядках всі числа додатні, то задача розв’язку немає.

Етап 3. Щоб перейти до наступного псевдоплану, треба вибрати розв’язуваний рядок і розв’язуваний стовпець. Вектор, що підлягає виведенню з базису, визначаємо так: серед від’ємних чисел стовпця A₀ вибираємо найбільше за абсолютною величиною значення. В нашому прикладі це 2. Таким чином, з базису виводимо вектор A₄. Рядок A₄ є розв’язуваним, його вилучаємо з базису.

Далі визначаємо, який вектор треба ввести в базис. Обчислюємо відношення компонент (m+1) рядка до відповідних від’ємних компонент вектора, який вводимо в базис A₄, і серед них обираємо найменше значення за абсолютною величиною

для всіх <0.

Маємо

Стовпець, який відповідає мінімальному відношенню, є вектор A₃, його вводимо в базис. Використовуючи жорданові виключення переходимо до нової симплекс-таблиці (табл. 10).

Таблиця 10

i	Базис		A0	C1=-8	C2=-8	C3=-20	C4=0	C5=0
				A1	A2	A3	A4	A5
1	A3	-20	1	0,5	-2	1	-0,5	0
2	A5	0	1	3	-5	0	-1	1
m+1			-20	-2	48	0	10	0

З табл. 8 видно, що отримано новий план двоїстої задачі Y(10;0). Значення цільової функції на цьому плані Отже, двоїстий симплекс-метод дає можливість здійснювати перехід від одного плану двоїстої задачі до іншого.

В стовпці немає від’ємних чисел, але в рядку оцінок є одне від’ємне число. Зробимо перетворення таблиці звичайним симплекс-методом (табл. 11).

Таблиця 11

i	Базис		A0	C1=-8	C2=-8	C3=-20	C4=0	C5=0
				A1	A2	A3	A4	A5
1	A3	-20	0,83333	0	-1,1667	1	-0,3333	-0,1667
2	A1	-8	0,33333	1	-1,6667	0	-0,3333	0,33333
m+1			-19,333	0	44,6667	0	9,33333	0,66667

Оскільки, всі оцінки а в стовпці немає від’ємних чисел, то в табл. 11 знайдено оптимальний план прямої та двоїстої задач. = (1/3, 0, 5/6, 0, 0) та = (28/3;2/3). На цих планах значення цільових функцій прямої та двоїстої задач рівні:

Шукане мінімальне значення задачі буде

Змінні двоїстої задачі, як зазначалось вище, позначають умовні двоїсті оцінки, які визначають дефіцитність.

Застосування двоїстого симплекс-методу особливо ефективне під час аналізу моделі на чутливість.