Розв’язання задачі лінійного програмування з використанням методу штучного базису

Мета – навчитися розв’язувати задачу лінійного програмування з використанням штучного базису

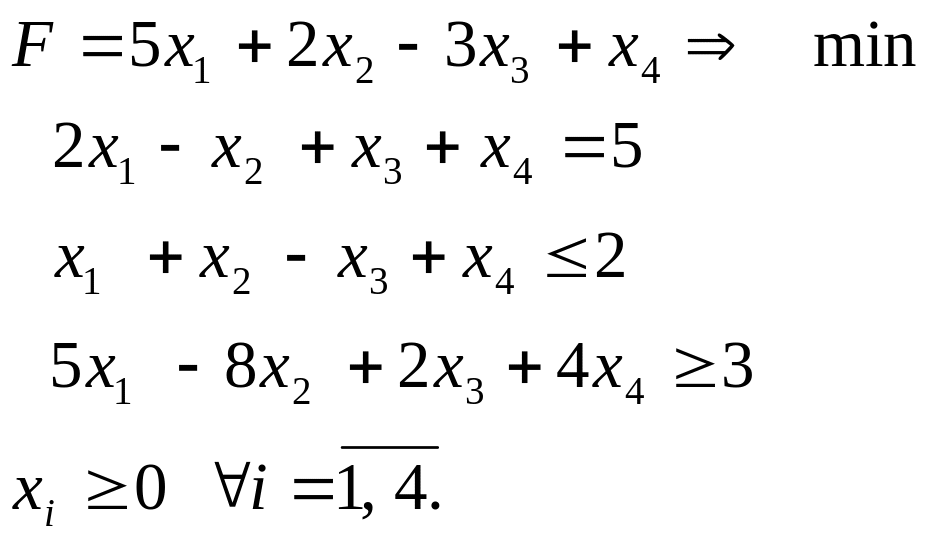
Зведемо задачу до канонічної форми:

Запишемо систему обмежень у векторній формі:

де

Кількість обмежень . Оскільки серед векторів немає ще двох одиничних векторів, то складаємо розширену задачу і вводимо штучні змінні .

де ─ деяке досить велике додатне число, конкретне значення якого не задається.

Вектори і одиничні, вони утворюють базис. Змінні і ─ базисні, змінні ─ вільні і прирівнюються до нуля. Опорний план розширеної задачі буде мати вигляд:

X_оп=(x₁=0; x₂=0; x₃=0; x₄=0; x₅=2; x₆=0; x₇=5; x₈=3;).

Використовуючи симплекс-метод для розширеної задачі, поступово вводимо в базис основні змінні замість штучних.

Після обмеженого числа ітерацій всі штучні змінні повинні бути виведені з базису.

Побудуємо симплекс-табл. 4.

Таблиця 4

i	Базис		A0	C1=-5	C2=-2	C3=3	C4=-1	C5=0	C6=0	C7=-M	C8=-M
				A1	A2	A3	A4	A5	A6	A7	A8
1	A7	-М	5	2	-1	1	1	0	0	1	0
2	A5	0	2	1	1	─1	1	1	0	0	0
3	A8	-M	3	5	-8	2	4	0	-1	0	1
m+1			0	5	2	-3	1	0	0	0	0
m+2			─8	─7	9	-3	-5	0	M	0	0

Обчислимо і :

У рядок записуємо числа без , а в рядок записуємо коефіцієнти при М.

Оскільки в рядку серед величин є від’ємні, то початковий опорний план розширеної задачі не є оптимальним. Треба перейти до наступного опорного плану. Обчислення виконуємо за допомогою симплекс-методу, однак розв’язуваний стовпець обираємо серед елементів рядка. Розв’язуваний стовпець відповідає найбільшому за абсолютною величиною від’ємному елементу рядка – це -7. Вектор, який вводиться, – . Знаходимо величину Розв’язуваний рядок – третій. Розв’язуваний елемент дорівнює 5.

Отже, з базису виведемо штучний вектор , коефіцієнти якого далі перераховувати не потрібно, а в базис вводимо вектор .

Використовуючи жорданові виключення перерахуємо елементи (табл.5).

Таблиця 5

i	Базис		A0	C1=-5	C2=-2	C3=3	C4=-1	C5=0	C6=0	C7=-M	C8=-M
				A1	A2	A3	A4	A5	A6	A7	A8
1	A7	-М	3,8	0	2,2	0,2	-0,6	0	0,4	1
2	A5	0	1,4	0	2,6	-1,4	0,2	1	0,2	0
3	A1	-5	0,6	1	-1,6	0,4	0,8	0	-0,2	0
m+1			-3	0	10	-2,6	-3	0	1	0
m+2			-3,8	0	-2,2	-0,2	-0,6	0	-0,4	0

Найбільше за абсолютною величиною від’ємне число рядка – -2,2. Вектор, який вводиться, – A₂. Знаходимо величину Розв’язуваний рядок – другий. Розв’язуваний елемент дорівнює 2,6. Отже, з базису виведемо вектор A₅.

Використовуючи жорданові виключення перерахуємо елементи (табл.6).

Таблиця 6

i	Ба-зис		A0	C1=-5	C2=-2	C3=3	C4=-1	C5=0	C6=0
				A1	A2	A3	A4	A5	A6
1	A7	-М	2,615385	0	0	1,38462	-0,7692	-0,8462	0,23077
2	A2	-2	0,538462	0	1	-0,5385	0,07692	0,38462	0,07692
3	A1	-5	1,461538	1	0	-0,4615	0,92308	0,61538	-0,0769
m+1			-2,7	0	0	0,38	-3,77	-3,846	0,23
m+2			-2,6	0	0	-1,38	-0,76	0,84	-0,23

Найбільше за абсолютною величиною від’ємне число рядка – -1,38. Вектор, який вводиться, – A₃. Знаходимо величину Розв’язуваний рядок – перший. Розв’язуваний елемент дорівнює 1,38462. Отже, з базису виведемо вектор A₇, коефіцієнти якого далі перераховувати не потрібно. Використовуючи жорданові виключення перерахуємо елементи (табл.7).

Таблиця 7

i	Базис		A0	C1=-5	C2=-2	C3=3	C4=-1	C5=0	C6=0
				A1	A2	A3	A4	A5	A6
1	A3	3	1,88889	0	0	1	-0,5556	-0,6111	0,16667
2	A2	-2	1,55556	0	1	0	-0,2222	0,05556	0,16667
3	A1	-5	2,33333	1	0	0	0,66667	0,33333	0
m+1			-9,1111	0	0	0	-3,5556	-3,6111	0,16667
m+2			0	0	0	0	0	0	0

Найбільше за абсолютною величиною від’ємне число (m+1) рядка – -3,61. Вектор, який вводиться, – A₄. Знаходимо величину Розв’язуваний рядок – третій. Розв’язуваний елемент дорівнює 0,33333. Отже, з базису виведемо вектор A₁. Використовуючи жорданові виключення перерахуємо елементи (табл.8).

Таблиця 8

i	Ба-зис		A0	C1=-5	C2=-2	C3=3	C4=-1	C5=0	C6=0
				A1	A2	A3	A4	A5	A6
1	A3	3	6,166667	1,83333	0	1	0,66667	0	0,16667
2	A2	-2	1,166667	-0,1667	1	0	-0,3333	0	0,16667
3	A5	0	7	3	0	0	2	1	0
m+1			16,16667	10,8333	0	0	3,66667	0	0,16667
m+2			0	0	0	0	0	0	0

У табл. 8 всі . Опорний план X_оп=(0; 1,166667; 6,166667; 0; 7; 0).

X_оп=(0; 1,166667; 6,166667; 0; 7; 0) є оптимальним планом задачі і . Оскільки початкова задача була на мінімум цільової функції, то .