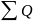График годового изменения альбедо (рис.5)

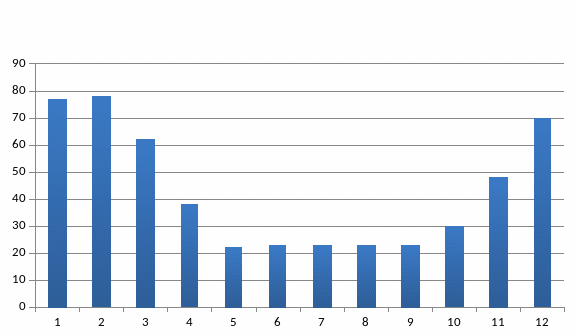
Распределение поглощенной и отраженной радиации (рис.6)

Месяц	1	2	3	4	5	6	7	8	9	10	11	12
	90	160	270	440	610	710	590	520	300	200	95	70

3. Тепловой режим почвы

Если почва однородна по вертикали, то ее температура /t/ на глубине Z в момент времени  определяется из уравнения теплопроводности (уравнение Фурье).

,

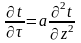где: а – температуропроводность, выражаемая в см²/ч с точностью до сотых.

Приближенно температуропроводность определяют по уменьшению амплитуды колебаний с глубиной

,

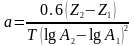где: Z₁ и Z₂ – глубины соответствующих слоев;

А₁ и А₂ – амплитуды на указанных глубинах.

Основными законами распространения температурных колебаний в почве являются следующие:

1. Закон неизменности периода колебаний с глубиной

Т(Z) = Const,

где: Z – глубина слоя.

2. Закон уменьшения амплитуды колебаний с глубиной

,

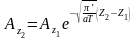где: Z₁ и Z₂ – глубины, на которых в разных почвах (а₁  а₂) амплитуды температурных колебаний с одинаковым периодом (Т₁ = Т₂) уменьшается в одинаковое число раз 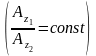и соотносятся между собой, как корни квадратные из температуропроводности этих почв.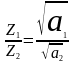

3. Закон сдвига фазы колебаний с глубиной (закон запаздывания)

,

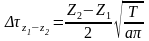где: Z₁ и Z₂ – глубины, на которых в одной и той же почве (а = Const) амплитуды температурных колебаний с разными периодами (Т₁  Т₂ ) уменьшаются в одинаковое число раз и относятся между собой, как корни квадратные из периодов колебаний.

.

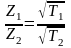3.1 Вычисление амплитуды колебаний почвы на разных глубинах и запаздывания максимума температуры

Исходные данные для вычисления амплитуды колебания почвы приведены в таблице №8.

Таблица 8

Глуби-на, м	Месяцы
0.2	-9.0	-9.0	–5.0	5.0	15.0	21.0	23.0	20.0	12.0	5.0	–2.0	–7.0
1.6	3.6	2.5	1.1	2.0	4.9	9.1	12.1	13.5	13.0	10.7	7.7	5.1
3.2	6.7	5.7	5.0	4.4	4.4	5.7	7.5	9.2	10.1	10.1	9.3	8.0

График годового хода температуры почвы на различных глубинах представлены на рис. 7.

Амплитуды колебаний температуры на различных глубинах определяются по графику, представленному на рис. 7.

Результаты сводятся в таблице №9.

Таблица 9

Амплитуда колебания температуры

Глубина, м	tmax	tmin	t
0,2	23,0	-9,0	32,0
1,6	13,5	1,1	12,7
3,2	10,1	4,4	5,7

Максимумы температуры по отношению к поверхности сдвинуты на глубине 1,6 м на один месяц, а на глубине 3,2 м – на два месяца.

На рис. 8 представлен график термоизоплет.

В нашем случае термоизоплеты – это линии, изображающие изменения температуры почвы во времени и в зависимости от глубины наблюдения.

Графики изменения температуры в зависимости от глубины в указанные сроки наблюдений приведены на рис. 9.

Вычисление градиентов температуры в различных слоях в сроки наблюдений сведены в таблицу 10. Градиент температуры в слое определяется как t/h, где t – разность температур, h – разность глубин. В нашем случае h = 1,4 м, 1,6 м.