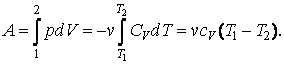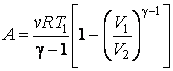- •Предмет молекулярная физика. Основные положения мкт и их анализ. Идеальный газ.
- •Статистический и термодинамический методы описания систем многих частиц. Основное уравнение молекулярно–кинетической теории идеального газа.
- •Температура. Молекулярно-кинетический смысл температуры. Основные понятия термометрии.
- •Уравнения состояние и законы идеального газа.
- •Распределение максвелла. Характерные скорости распределения максвелла и их сравнение (вывод).
- •13.Задачи термодинамики. Нулевое начало. Внутренняя энергия тел. Внутренняя энергия.
- •15. Работа в термодинамике. Вычисление работы в изопроцессах иг.
- •Теплота. Теплоёмкость. Общее выражение для теплоёмкости. Теплоёмкость иг в изопроцессах.
- •17.Первое начало термодинамики и его различные формулировки
- •19.Адиабатный процесс. Уравнение адиабаты (вывод).
- •22 Второе начало термодинамики и его различные формулировки.
- •24. Первая теорема карно. (доказательство)
- •Вторая теорема карно. Неравенство клаузиуса.
- •Энтропия как функция состояния.
- •Изменение энтропии в иг.
- •30.Метод термодинамических потенциалов. Внутренняя энергия и свободная энергия Гельмгольца.
- •31.Метод термодинамических потенциалов. Энтальпия и потенциал Гиббса.
- •32.Соотношение взаимности Максвелла и их значение.
- •33.Критерии устойчивости термодинамических систем. Принцип Ле Шателье-Брауна. Общие критерии термодинамической устойчивости
- •Принцип Ле-Шателье – Брауна
- •34.Различные формы уравнения состояния реального газа. Уравнение Ван-дер-Ваальса. Изотермы реального газа.
- •35.Изотермы газа Ван-дер-Ваальса. Метастабильные состояния.
- •36.Критические состояния. Свойства вещества в критическом состоянии.
- •37.Приведенное уравнение Ван-дер-Ваальса.
- •38.Внутренняя энергия газа Ван-дер-Ваальса.
- •41.Эффект Джоуля-Томсона. Интегральный коэффициент дросселирования (a0; b 0). Температура инверсии.
- •42.Поверхностное натяжение. Энергетический и динамический смысл коэффициента поверхностного натяжения. Методы определения.
- •43.Условия равновесия на границе двух сред (жидкость жидкость).
- •44.Условия равновесия на границе двух сред (жидкость тв. Тело). Смачивание.
- •45.Давление под искривлённой поверхностью. Капилляры и капиллярные явления. Формула Лапласа.
- •46.Фазы и фазовые превращения. Условия равновесия двух фаз химически однородного вещества.
- •47. Диаграмма состояния. Тройная точка. Равновесие трёх фаз химически однородного вещества.
- •48. Уравнение Клапейрона-Клаузиуса. Фазовые переходы.
- •49. Динамическое равновесие на границе жидкость-пар. Зависимость давления насыщенного пара от температуры.
- •53.Процессы переноса,их природа.Общее ур-е процессов переноса.
- •54.Вязкость. Закон Ньютона для вязкого трения. Коэффициент вязкости и способы его измерения.
- •55.Теплопроводность.Закон Фурье.Коэфф. Теплопроводности.
- •56.Диффузия.Закон Фика.Коэфф. Диффузии. Связь между коэфф-ми процессов переноса.
19.Адиабатный процесс. Уравнение адиабаты (вывод).
Адиабатным называют такой процесс, в котором к системе не подво-дится тепло и от системы не отводится тепло. При адиабатном процессе должна быть обеспечена идеальная теплоизоляция от внешней среды, в отличие от изотермического процесса, требующего идеального теплового контакта со средой. В реальных условиях процесс является адиабатным, если система снабжена хорошей теплоизоляцией или если процесс протекает настолько быстро, что не происходит заметного теплообмена с внешней средой.
Из первого закона термодинамики следует,
что при адиабатном процессе
![]() работа
производится только за счет изменения
внутренней энергии вещества:
работа
производится только за счет изменения
внутренней энергии вещества:
|
(4.9.1) |
Можно записать и в интегральной форме:
|
(4.9.2) |
Если вещество расширяется и совершает
работу над внешними телами, то
![]() и,
как следует ,
и,
как следует ,
![]() ,
т. е. внутренняя энергия вещества
уменьшается. Это и понятно: в адиабатном
процессе к системе нет притока теплоты
извне и единственный источник энергии
для совершения работы – это внутренняя
энергия самой системы. Соотношения
справедливы для любых адиабатных
процессов: равновесных или неравновесных,
для любых веществ, находящихся в любых
агрегатных состояниях, так как они
являются следствием закона сохранения
энергии.
,
т. е. внутренняя энергия вещества
уменьшается. Это и понятно: в адиабатном
процессе к системе нет притока теплоты
извне и единственный источник энергии
для совершения работы – это внутренняя
энергия самой системы. Соотношения
справедливы для любых адиабатных
процессов: равновесных или неравновесных,
для любых веществ, находящихся в любых
агрегатных состояниях, так как они
являются следствием закона сохранения
энергии.
Для идеального газа:
|
(4.9.3) |
Отсюда видно, что при адиабатном
расширении
![]() газ
охлаждается
газ
охлаждается
![]() ,
а при адиабатном сжатии
,
а при адиабатном сжатии
![]() газ
нагревается
газ
нагревается
![]() ,
хотя теплота при этом процессе не
подводится и не отводится.
,
хотя теплота при этом процессе не
подводится и не отводится.
Проинтегрировав, найдем работу, совершаемую идеальным газом при адиабатном процессе.
|
(4.9.4) |
Теплоемкость
![]() вынесена
из-под интеграла, т. к. для идеального
газа она не зависит от температуры.
вынесена
из-под интеграла, т. к. для идеального
газа она не зависит от температуры.
Чтобы найти уравнение адиабаты в
переменных
![]() подставим
вместо p его выражение из уравнения
Менделеева –Клапейрона
подставим
вместо p его выражение из уравнения
Менделеева –Клапейрона
![]() В
результате будем иметь
В
результате будем иметь
|
(4.9.5) |
Интегрирование последнего соотношения дает
|
(4.9.6) |
Откуда находим
|
(4.9.7) |
Выразим величину
![]() через
отношение теплоемкостей
через
отношение теплоемкостей
![]() В
результате будем иметь
В
результате будем иметь
![]() Подставив,
получим
Подставив,
получим
|
(4.9.8) |
Последнее соотношение есть уравнение адиабаты (уравнение Пуассона) в переменных T,V. Чтобы записать это уравнение в координатах p,V или T,p нужно произвести замену соответствующих переменных , воспользовавшись уравнением Менделеева – Клапейрона. В результате получим еще два эквивалентных уравнения адиабаты:
|
(4.9.9) |
|
(4.9.10) |
Выражение для работы можно записать иначе. Для этого уравнение адиабаты представим в виде:
|
(4.9.11) |
Отсюда находим
|
(4.9.12) |
Подставляя, и учитывая что
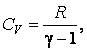 получим
получим
|
(4.9.13) |
Из уравнения Пуассона (4.9.9) следует, что
давление идеального газа в адиабатном
процессе
![]() убывает
быстрее, чем в изотермическом процессе
убывает
быстрее, чем в изотермическом процессе
![]() ,
так как всегда
,
так как всегда
![]() и,
таким образом,
и,
таким образом,![]() . Физически это объясняется тем, что при
адиабатном расширении давление газа
уменьшается не только за счет уменьшения
объема, но и по причине происходящего
при этом понижении температуры. Поэтому
и работа против меньшего внешнего
давления
. Физически это объясняется тем, что при
адиабатном расширении давление газа
уменьшается не только за счет уменьшения
объема, но и по причине происходящего
при этом понижении температуры. Поэтому
и работа против меньшего внешнего
давления
![]() (
(
![]() для
равновесного процесса) при адиабатном
процессе будет меньше, чем работа против
большего внешнего давления
для
равновесного процесса) при адиабатном
процессе будет меньше, чем работа против
большего внешнего давления
![]() при
изотермическом процессе. На рис. 1 работа
расширения от объема
при
изотермическом процессе. На рис. 1 работа
расширения от объема
![]() до
объема
до
объема
![]() при
адиабатном процессе равна площади
фигуры
при
адиабатном процессе равна площади
фигуры
![]() ,
а при изотермическом – площади фигуры
,
а при изотермическом – площади фигуры
![]() .
.
|
рис. 1 |
Наоборот, при адиабатном сжатии от
объема
до
объема
![]() давление
газа растет быстрее, чем при изотермическом
процессе, так как при адиабатном процессе
давление увеличивается не только за
счет уменьшения объема, но и вследствие
роста температуры газа. Поэтому и работа
при адиабатическом сжатии, равная
площади фигуры
давление
газа растет быстрее, чем при изотермическом
процессе, так как при адиабатном процессе
давление увеличивается не только за
счет уменьшения объема, но и вследствие
роста температуры газа. Поэтому и работа
при адиабатическом сжатии, равная
площади фигуры
![]() больше
работы сжатия при изотермическом
процессе, равной площади фигуры
больше
работы сжатия при изотермическом
процессе, равной площади фигуры
![]() .
.
21 ПОЛИТРОПНЫЕ ПРОЦЕССЫ. УРАВНЕНИЕ ПОЛИТРОПНЫ (ВЫВОД).
Политропический процесс — термодинамический процесс, во время которого удельная теплоёмкость c газа остаётся неизменной. Предельными частными явлениями политропного процесса являются изотермический процесс и адиабатный процесс. В случае идеального газа изобарный процесс и изохорный процесс также являются политропическими.
Для идеального газа уравнение политропы может быть записано в виде:
pVn = const
где величина
![]() называется показателем политропы.
называется показателем политропы.
В зависимости от процесса можно определить значение n:
1. Изотермический процесс: n = 1, так как PV1 = const, значит PV = const, значит T = const.
2. Изобарный процесс: n = 0, так как PV0 = P = const.
3. Адиабатный процесс: n = γ, это следует из уравнения Пуассона.
4. Изохорный процесс:
![]() ,
так как
,
так как
![]() ,
значит P1 / P2 = (V2 / V1)n, значит V2 / V1 = (P1 / P2)(1
/ n), значит, чтобы P1 и P2 обратились в 1, n
должна быть бесконечность.
,
значит P1 / P2 = (V2 / V1)n, значит V2 / V1 = (P1 / P2)(1
/ n), значит, чтобы P1 и P2 обратились в 1, n
должна быть бесконечность.