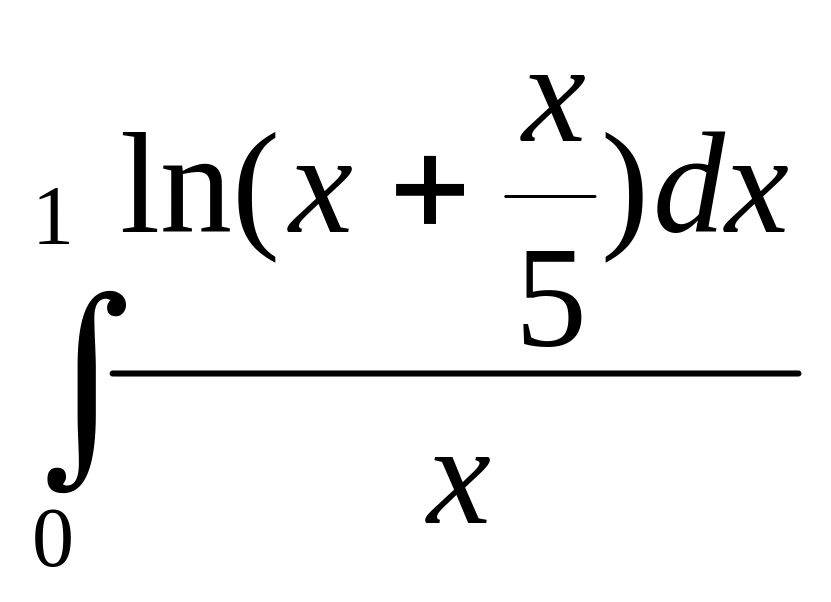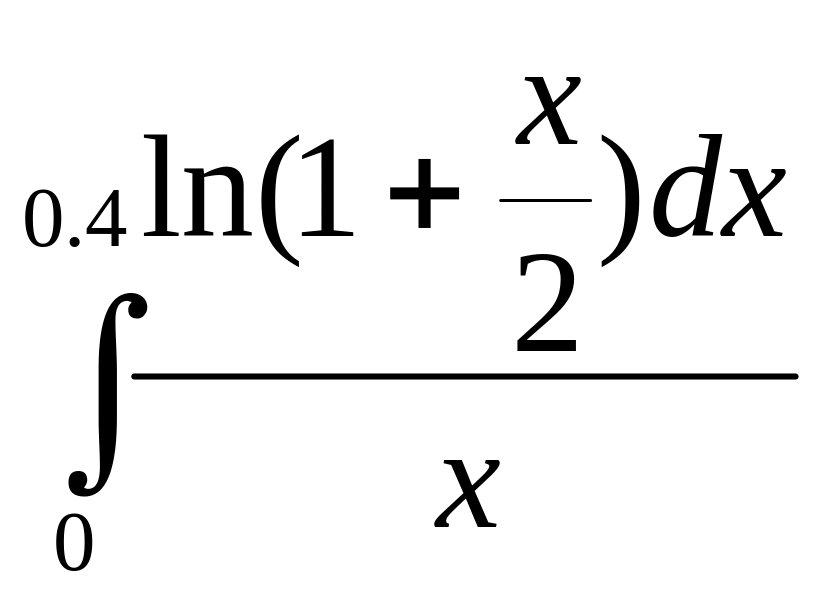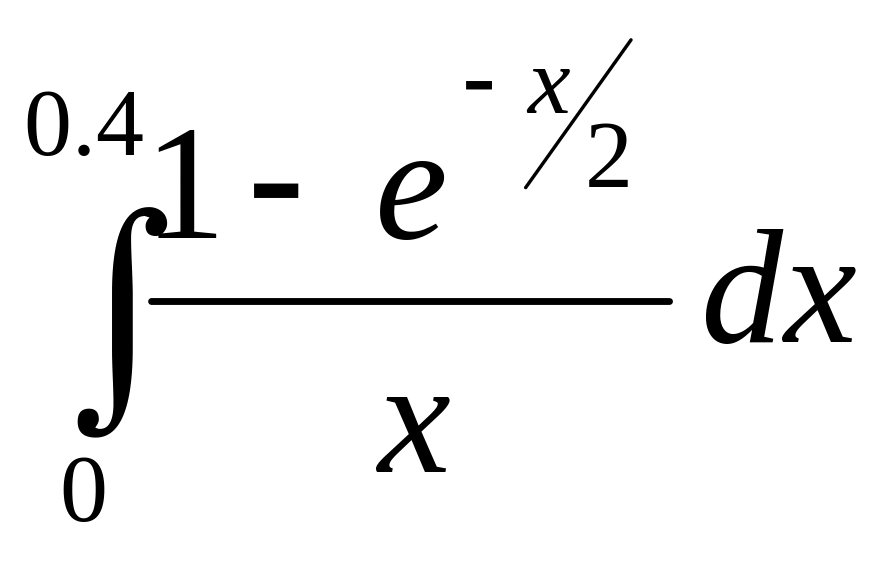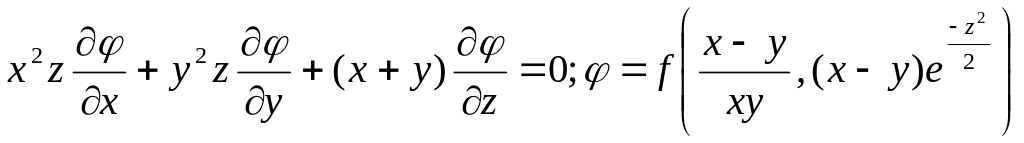- •Методические указания и задания
- •95007, Симферополь, Ялтинская 4,
- •2. Исследовать следующие ряды на сходимость.
- •3. Вычислить сумму ряда с точностью до :
- •4. Найти область сходимости степенного ряда:
- •5. Разложить функцию по формуле Маклорена , используя известные разложения:
- •6. Вычислить интеграл с точностью 0,001:
- •Функции многих переменных.
- •1. Найти и изобразить область определения функции:
- •2. Найти du, если:
- •3. Найти и от функций, заданных неявно в точке м0:
- •4. Проверить равенство смешенных производных для заданной функции:
- •7. Написать уравнение касательной плоскости и нормали к поверхности в заданной точке:
- •8. Исследовать функцию на экстремум:
- •9. Найти наибольшее и наименьшее значение функции
- •10. Приближенно вычислить с помощью дифференциала:
- •11. Найти условные экстремумы функции относительно заданного уравнения связи:
- •1. Вычислить несобственные интегралы (или установить их расходимость), пользуясь определением:
- •3. Исследовать на абсолютную и условную сходимость:
4. Найти область сходимости степенного ряда:
1. |
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11. |
12. |
13.
|
14.
|
15.
|
16. |
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
23.
|
24.
|
5. Разложить функцию по формуле Маклорена , используя известные разложения:
1.
f(x)= |
2.
f(x)= |
3.
f(x)= |
4.
f(x)= |
5.
f(x)= |
6.
f(x)= |
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
23.
|
24.
|
25.
|
26.
|
27.
|
|
6. Вычислить интеграл с точностью 0,001:
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
23.
|
24.
|
25.
|
26.
|
Функции многих переменных.
1. Найти и изобразить область определения функции:
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
4. ![]() .
.
5. ![]() .
.
6. ![]() .
.
7. ![]() .
.
8. ![]() .
.
9. ![]() .
.
10. ![]() .
.
11. ![]() .
.
12. ![]() .
.
13. ![]() .
.
14. ![]() .
.
15. ![]() .
.
16. ![]() .
.
17. ![]() .
.
18. ![]() .
.
19. ![]() .
.
20. ![]() .
.
21. ![]() .
.
22. ![]() .
.
23. ![]() .
.
24. ![]() .
.
25. ![]() .
.
2. Найти du, если:
1. |
2. |
3. |
4. |
5. |
6. |
7. |
8. |
9. |
10. |
11. |
12. |
13. |
14. |
15. |
16. |
17. |
18. |
19. |
20. |
21. |
22. |
23. |
24.
|
25.
|
|
3. Найти и от функций, заданных неявно в точке м0:
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]() .
.
6.
![]() .
.
7.
![]() .
.
8.
![]() .
.
9.
![]() .
.
10.
![]() .
.
11.
![]() .
.
12.
![]() .
.
13.
![]() .
.
14.
![]() .
.
15.
![]() .
.
16.
![]() .
.
17.
![]() .
.
18.
![]() .
.
19.
![]() .
.
20.
![]() .
.
21.
![]() .
.
22.
![]() .
.
23.
![]() .
.
24.
![]() .
.
25.
![]() .
.
4. Проверить равенство смешенных производных для заданной функции:
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
23.
|
24.
|
25. |
|
5.
Найти полные дифференциалы I и II порядка
от сложной функции
![]() ,
если:
,
если:
1.
|
2. |
3.
|
4.
|
5. |
6. |
7.
|
8. |
9.
|
10. |
11.
|
12. |
13.
|
14.
|
15.
|
16.
|
17. |
18. |
19.
|
20.
|
21.
|
22. |
23. |
24. |
25.
|
|
6. Проверить равенство :
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
23.
|
24.
|
25.
|