8. Найти общее решение дифференциального уравнения

Решение. Дано линейное однородное уравнение четвертого порядка с постоянными коэффициентами. В соответствии с общим методом решения таких уравнений составим характеристическое уравнение

.

Разложим левую часть уравнения на простейшие множители:

.

Видно, что уравнение имеет два действительных корня и . Кратность каждого из них равна 2. Фундаментальная система решений состоит из четырех функций:

; ; ;

Общее решение уравнения есть произвольная линейная комбинация этих решений:

Ответ:

9. Решить дифференциальное уравнение методом Лагранжа

Решение. Рассматривается неоднородное линейное уравнение второго порядка с постоянными коэффициентами. Метод Лагранжа, или метод вариации произвольных постоянных, состоит в том, что сначала находят общее решение соответствующего однородного уравнения, а затем общее решение неоднородного уравнения ищут в специальном виде. А именно, в таком же виде, как и общее решение соответствующего однородного уравнения, но считая коэффициенты не постоянными, а неизвестными функциями, которые находят так, чтобы неоднородное уравнение при подстановке обращалось в тождество. Используем этот метод для решения данного уравнения.

Соответствующее однородное уравнение

Характеристическое уравнение

имеет корни , , так что общее решение однородного уравнения

Тогда общее решение неоднородного уравнения будем искать в виде

.

Для нахождения функций и составим известную из теории систему

,

которая в нашем примере имеет вид

.

Умножим первое уравнение на , второе – на и сложим полученные уравнения. Тогда

,

то есть

, а .

Здесь - произвольная постоянная.

Из первого уравнения системы получим: , откуда

.

Тогда

Ответ:

10. Найти общее решение дифференциального уравнения

Решение. Данное неоднородное линейное уравнение второго порядка с постоянными коэффициентами имеет правую часть такого вида, что можно искать частное решение неоднородного уравнения по виду функции – правой части. Найдем сначала общее решение соответствующего однородного линейного уравнения

.

Характеристическое уравнение имеет действительный корень 6 кратности 2. Поэтому общее решение однородного уравнения имеет вид

Частное решение неоднородного уравнения будем искать в виде ,

так как есть функция вида и число не является корнем характеристического уравнения. Найдем

,

и подставим вместе с в неоднородное уравнение:

.

Для того чтобы равенство тождественно выполнялось, коэффициенты при функциях и в левой и правой части должны совпадать. Это условие выражено системой уравнений

, или ,

решая которую, получим A=16/25, В=-12/25.

Общее решение неоднородного линейного уравнения есть сумма общего решения соответствующего однородного и любого частного решения неоднородного. Складывая, получаем:

Ответ:

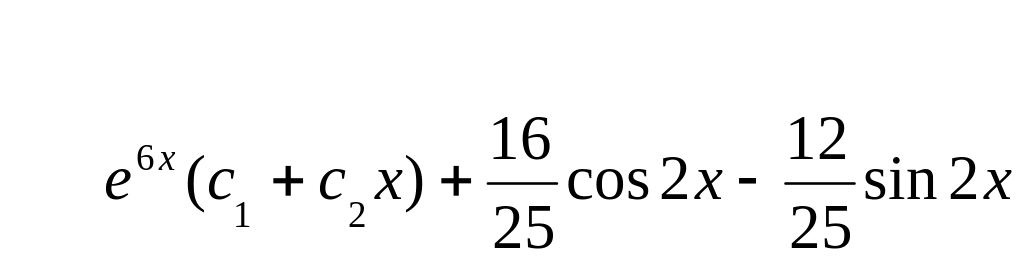
Тема 2. Ряды

1. Исследовать сходимость числового ряда .

Решение. Воспользуемся вторым (предельным) признаком сравнения для положительных числовых рядов. Вместе с данным рядом

(1) рассмотрим ряд (2).

Общий член ряда (1) , общий член ряда (2) .

Найдем

.

Так как этот предел конечный и не равен нулю, то оба ряда сходятся или расходятся одновременно. Но ряд (2) сходится как ряд Дирихле при (по интегральному признаку: , несобственный интеграл сходится, поэтому сходится и ряд (2)).

Ответ: данный ряд (1) сходится.

2. Исследовать сходимость числового ряда .

Решение. Воспользуемся признаком Даламбера для положительных числовых рядов. Общий член данного ряда . Следующий за п-ным членом . Найдем

.

Так как найденный предел меньше 1, то по признаку Даламбера ряд сходится.

Ответ: данный ряд сходится.

3. Исследовать сходимость знакочередующегося числового ряда . В случае сходимости исследовать на абсолютную и условную сходимость.

Решение. Воспользуемся признаком Лейбница для знакочередующихся числовых рядов. Согласно этому признаку ряд сходится, если

1) ;

2) числовая последовательность является монотонно убывающей.

Для данного ряда оба условия выполнены:

1) ;

2) , . Верно неравенство .

Поэтому ряд сходится по признаку Лейбница.

Составим ряд из модулей членов данного ряда: . Этот ряд расходится, так как является рядом Дирихле с . Поэтому исходный ряд не сходится абсолютно. Его сходимость является условной.

Ответ: данный ряд сходится условно.

4. Определить область сходимости степенного ряда .

Решение. Рассматривается ряд вида , где числовой коэффициент . Найдем радиус сходимости ряда по формуле :

.

То есть интервал сходимости данного ряда (-1; 1). Исследуем сходимость ряда на концах интервала.

Пусть х=-1. Тогда получаем знакочередующийся числовой ряд . Этот ряд расходится, так как не выполнено необходимое условие сходимости числового ряда: если ряд сходится, то . По этой же причине не сходится и ряд, полученный при х=1: , .

Ответ: область сходимости данного ряда – интервал (-1; 1).

5. Определить область сходимости степенного ряда .

Решение. Обозначим , и будем рассматривать данный ряд как степенной по степеням у. Найдем его радиус сходимости, , :

.

Тогда ряд сходится при , то есть на интервале (2; 4) изменения переменной х. Исследуем сходимость на концах интервала. Пусть х=4. Получаем числовой ряд . Этот положительный ряд сходится по второму признаку сравнения со сходящимся рядом Дирихле , :

.

Так как предел конечный и он отличен от нуля, то исследуемый ряд сходится вместе с рядом Дирихле.

При подстановке в степенной ряд х=2 получаем знакочередующийся ряд . Ряд, составленный из модулей его членов только что исследован. Он сходится. Поэтому данный знакочередующийся ряд сходится абсолютно.

Ответ: Область сходимости данного степенного ряда – отрезок [2; 4].

6. Найти четыре первых, отличных от нуля, члена разложения в ряд функции по степеням ,

Решение. 1-й способ. Если функция имеет производные достаточно высокого порядка в окрестности точки , то первые члены разложения ее в степенной ряд можно непосредственно найти по формуле (ряд Тейлора для ):

Найдем

Все найденные значения отличны от нуля. Поэтому первые четыре члена

искомого разложения образуют сумму

2-й способ. Можно воспользоваться известным разложением в биномиальной ряд

(*)

Преобразуем функцию к виду

и используем формулу (*), полагая в ней . Получим тот же результат, что и первым способом.

Ответ: Первые четыре члена разложения функции в ряд

7. Разложить функцию в ряд по степеням , используя разложения основных элементарных функций.

Решение. Преобразуем функцию к виду

и воспользуемся стандартными разложениями

Тогда получаем степенной ряд, в котором чередуются члены этих рядов с коэффициентами cos и sin :

Ответ:

8. Вычислить с помощью ряда определенный интеграл с точностью до 0.001.

Решение. По-видимому, в условиях допущена ошибка, так как данный интеграл – несобственный (так как ), и он расходится. Если бы в числителе подынтегральной функции был знак «-», то интеграл бы сходился. Тогда (бы!) используя стандартное разложение

,

мы разложили бы подынтегральную функцию в ряд

и проинтегрировали данный сходящийся степенной ряд почленно:

Далее, находя последовательно каждый член этого ряда, будем оценивать его, так как остаток знакочередующегося сходящегося ряда не превосходит по модулю первого отброшенного члена.

;

;

.

Итак, с точностью до 0.001

.

9. Найти первые четыре члена разложения в степенной ряд решения дифференциального уравнения при начальных условиях , .

Решение. Будем искать решение дифференциального уравнения в виде суммы его ряда Тейлора по степеням х-1:

Первые два члена уже найдены в силу начальных условий. Чтобы найти , подставим в дифференциальное уравнение значение х=1, тогда

.

Чтобы найти , продифференцируем данное дифференциальное уравнение и подставим в полученное уравнение значение х=1, тогда

.

Четыре члена разложения уже найдены. Но два из них равны 0. Чтобы найти 4 ненулевых члена разложения, нужно продолжить дифференцировать обе части дифференциального уравнения.

;

Ответ:

10. Разложить в ряд Фурье функцию f(x) на интервале [-, ],

Решение. Заданная функция кусочно-монотонна и ограничена, поэтому она допускает разложение в ряд Фурье

,

где

Найдем эти коэффициенты. Так как функция равна нулю на интервале (0, ], будем считать верхний предел интегрирования равным нулю.

;

Ответ: всюду внутри интервала (-, ), кроме х=0. На концах интервала и при х=0 значения функции находятся непосредственно из ее задания. Они не совпадают со значениями суммы ряда S(x), которые, как известно из теории, в точках разрыва функции равны:

, то есть ; ;