
- •Тема 1. Дифференциальные уравнения
- •2. Найти общее решение дифференциального уравнения
- •3. Найти общее решение дифференциального уравнения
- •4. Найти общее решение дифференциального уравнения
- •5. Найти общее решение дифференциального уравнения
- •6. Найти общее решение дифференциального уравнения
- •8. Найти общее решение дифференциального уравнения
- •10. Найти общее решение дифференциального уравнения
- •Тема 2. Ряды
Контрольная работа №2
Вариант 11
Тема 1. Дифференциальные уравнения
1. Найти общее решение дифференциального уравнения
![]()
Решение. Это уравнение с разделяющимися переменными:
![]()
Преобразуем его
к виду с разделенными переменными,
разделив на
![]() :
:
![]()
Проинтегрируем последнее равенство:
![]()
![]()
![]()
Ответ:
![]() - общий интеграл данного дифференциального
уравнения.
- общий интеграл данного дифференциального
уравнения.
2. Найти общее решение дифференциального уравнения
![]()
Решение. Разделим обе части уравнения на х. Тогда видно, что это однородное уравнение:
![]() .
.
Введем новую
функцию
![]() или
или
![]() .
Тогда
.
Тогда
![]()
![]() .
Подставляя в уравнение, получим
.
Подставляя в уравнение, получим
![]()
![]()
![]() - уравнение с
разделяющимися переменными. Решим его:
- уравнение с
разделяющимися переменными. Решим его:
![]()
![]()
![]()
![]()
![]()
![]()
![]() - общий интеграл
данного дифференциального уравнения.
- общий интеграл
данного дифференциального уравнения.
![]()
Ответ:
![]() - общее решение уравнения
- общее решение уравнения
3. Найти общее решение дифференциального уравнения
![]()
Решение. Это линейное уравнение, так как неизвестная функция у(х) и ее производная входят в него в первой степени. Будем искать у(х) в виде
![]() .
Тогда
.
Тогда
![]() .
Подставив в уравнение, получим:
.
Подставив в уравнение, получим:
![]() .
.
Сгруппируем слагаемые:
![]() (*)
(*)
и найдем и(х) такую, что
![]()
Последнее уравнение – с разделяющимися переменными:
![]()
![]()
![]()
![]()
![]() .
Выберем одну из первообразных
.
Выберем одну из первообразных
![]() .
Тогда v(x)
найдем так, чтобы равенство (*) выполнялось
с найденным и(х):
.
Тогда v(x)
найдем так, чтобы равенство (*) выполнялось
с найденным и(х):
![]()
![]()
![]()
![]()
Следовательно,
![]()
Ответ:
![]() - общее решение уравнения
- общее решение уравнения
4. Найти общее решение дифференциального уравнения
![]()
Решение.
Это уравнение Бернулли. Разделим его
на
![]() :
:
![]() .
.
Сделаем замену
![]() .
Тогда
.
Тогда
![]() .
Подставив в уравнение, получим:
.
Подставив в уравнение, получим:
![]()
- линейное уравнение
относительно z(x).
Решим его так же, как в задаче 3:
![]() .
Тогда
.
Тогда
![]() .
Подставив в уравнение, получим:
.
Подставив в уравнение, получим:
![]() .
.
Сгруппируем слагаемые:
![]() (*)
(*)
и найдем и(х) такую, что
![]()
Последнее уравнение – с разделяющимися переменными:
![]()
![]()
![]()
![]()
![]() ,
,
![]() .
Выберем одну из первообразных
.
Выберем одну из первообразных
![]() и v(x)
найдем так, чтобы равенство (*) выполнялось
с найденным и(х):
и v(x)
найдем так, чтобы равенство (*) выполнялось
с найденным и(х):
![]()
![]()
![]()
![]()
Из последней цепочки равенств видно, что
![]() .
.
Отсюда
![]() ,
,
и
![]()
Но тогда
![]() ,
,
а
![]()
Ответ:
![]()
5. Найти общее решение дифференциального уравнения
![]()
Решение. Это уравнение вида
![]() ,
,
где
![]() ,
,
![]() .
Так как
.
Так как
![]() ,
то есть
,
то есть
![]() ,
,
то данное уравнение есть уравнение в полных дифференциалах. Оно может быть записано в виде
![]() ,
,
где
![]() (**)
(**)
Но тогда общим интегралом этого уравнения будет равенство
![]() .
.
Найдем функцию F(x,y), используя условия (**):
![]()
![]() .
Для того, чтобы это была одна и та же
функция, нужно
.
Для того, чтобы это была одна и та же
функция, нужно
![]() ,
,
где С – произвольная постоянная.
Ответ:
![]() - общий интеграл данного уравнения.
- общий интеграл данного уравнения.
6. Найти общее решение дифференциального уравнения
![]()
Решение.
Это уравнение второго порядка, не
содержащее в записи переменную х.
Оно допускает понижение порядка в
предположении, что
![]() ,
где р
– некоторая функция, а у(х)
– искомое решение. При этом
,
где р
– некоторая функция, а у(х)
– искомое решение. При этом
![]() .
Уравнение после замены примет вид
.
Уравнение после замены примет вид
![]() - уравнение с
разделяющимися переменными. Решим его.
- уравнение с
разделяющимися переменными. Решим его.
![]()
![]() или
или
![]()
или
![]()
![]()
![]()
![]()
Таким образом,
![]() или
или
![]() .
.
Решение первого
из этих уравнений
![]() .
Второе из них – уравнение с разделяющимися
переменными. Решим его:
.
Второе из них – уравнение с разделяющимися
переменными. Решим его:
![]()
![]()
![]()
![]()
![]()
Ответ:
;
,
где
![]() - произвольные постоянные.
- произвольные постоянные.
7. Найти решение задачи Коши
![]()
Решение.
Уравнение допускает понижение порядка.
Обозначим
![]() .
Тогда
.
Тогда
![]() и уравнение примет вид:
и уравнение примет вид:
![]()
Это линейное уравнение 1-го порядка. Решим его, как задачу 3. Будем искать р(х) в виде
![]() .
Тогда
.
Тогда
![]() .
Подставив в уравнение, получим:
.
Подставив в уравнение, получим:
![]() .
.
Сгруппируем слагаемые:
![]() (*)
(*)
и найдем и(х) такую, что
![]()
Последнее уравнение – с разделяющимися переменными:
![]()
![]()
![]()
![]()
![]() .
Выберем одну из первообразных
.
Выберем одну из первообразных
![]() .
Тогда v(x)
найдем так, чтобы равенство (*) выполнялось
с найденным и(х):
.
Тогда v(x)
найдем так, чтобы равенство (*) выполнялось
с найденным и(х):
![]()
![]()
![]()
![]()
Следовательно,
![]()
Исключим произвольную
постоянную с,
используя начальное условие. Для этого
подставим в последнее равенство
![]() и
и
![]() .
Получим
.
Получим
![]()
![]()
![]()
![]()
Итак,
![]() .
.
Тогда
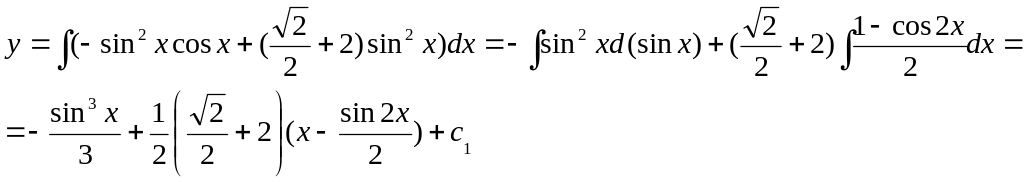
Остается найти
значение
![]() ,
используя начальное условие
,
используя начальное условие
![]() при
:
при
:
![]()
Отсюда
![]()
Ответ:
![]()
