3.4 Розрахунок пропускної здатності мережі

Мережа центрального офісу налічує 10 робочих станцій і 4 сервера. Від однієї станції надходить 63400 кадрів. Мережа працює цілодобово, в час найбільшого навантаження передається 20% від всього

числа кадрів, що передаються.

За годину через вузол мережі проходить:

• при Гаусовому розподілі N = 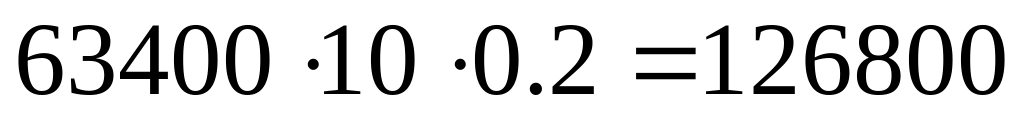кадрів;

• при нормальному розподілі N = 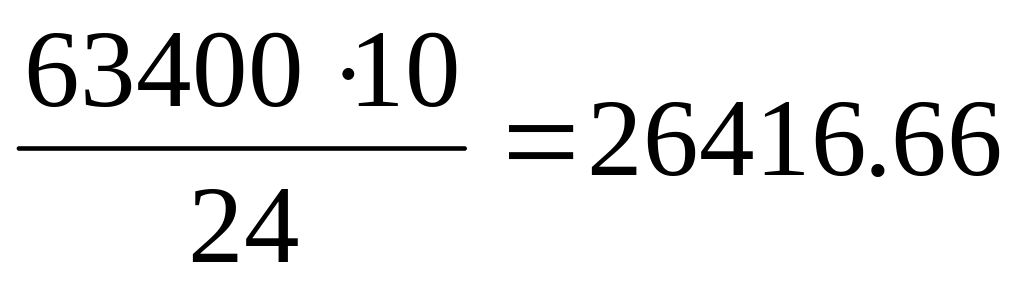кадрів.

Швидкість надходження кадрів знайдемо шляхом ділення отриманих чисел на 3600:

• при Гаусовому розподілі 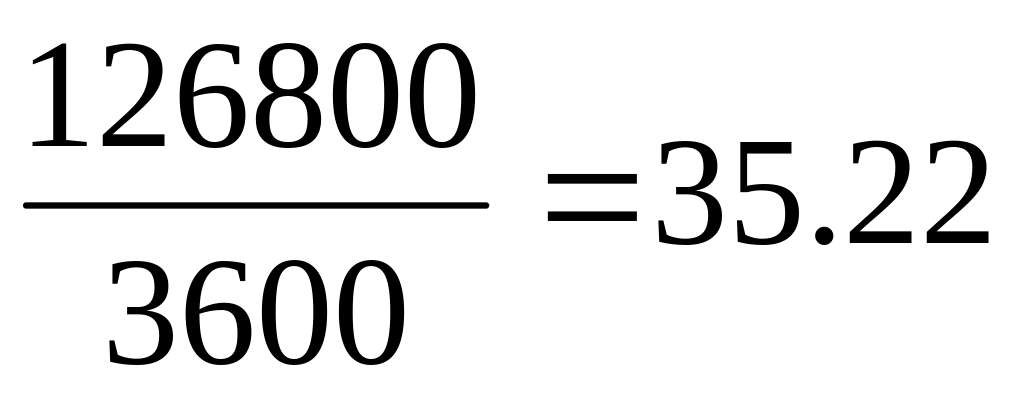кадр/сек;

• при нормальному розподілі 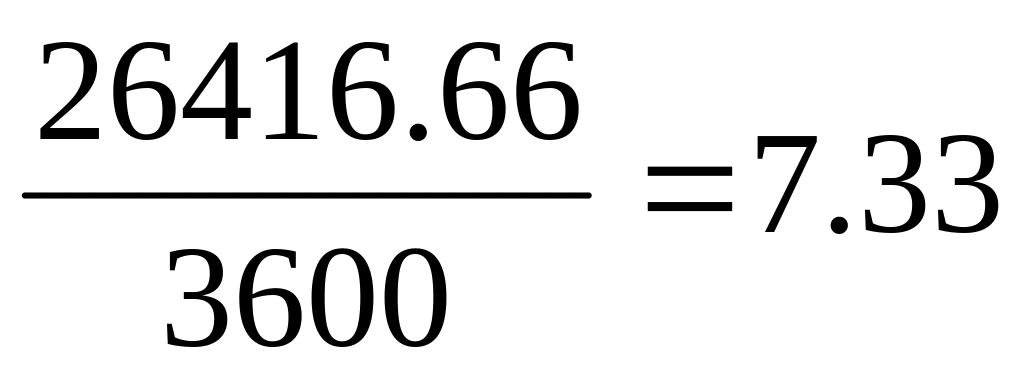кадр/сек.

Для розрахунку середньої швидкості обслуговування слід задатися певним значенням швидкості роботи глобальної мережі. Швидкість обміну інформацією в глобальній мережі дорівнює 2 Мбіт/с, або 2097152 біт/с. Тоді час, необхідний для передачі одного кадру довжиною 500 байт, складе 0,002 секунди.

Отже очікуваний час обслуговування рівний 0,002 секунди, тоді середня швидкість обслуговування (величина, зворотня до очікуваного часу обслуговування) складе 2000 кадрів за секунду.

З розрахунків виходить, що при таких швидкостях обслуговування і надходження кадрів даний канал справиться з трафіком, що надходить.

Ступінь використання технічних можливостей обслуговуючого пристрою (P) в системі можна визначити, поділивши середню швидкість надходження заявок на середню швидкість обслуговування:

• при Гаусовому розподілі Р = , тобто 1.76%;

• при нормальному розподілі Р = 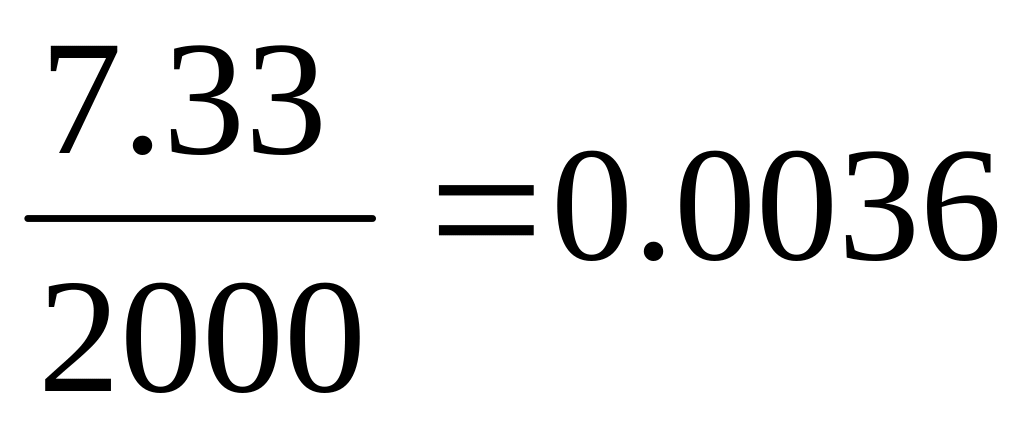, тобто 0. 36%.

Знаючи ступінь використання обслуговуючого пристрою, можна легко визначити вірогідність відсутності заявок (кадрів) в даний момент

часу P₀: P₀ = 1 - P.

• при Гаусовому розподілі P₀ = 1 – 0.0176 = 0,98 = 98%;

• при нормальному розподілі P₀ = 1 – 0.0036 = 0,99 = 99%.

Визначимо середнє число об'єктів в черзі, у теорії масового обслуговування середнє число об'єктів (unit) в системі зазвичай позначається L, а середнє число об'єктів в черзі - L_q. Для одноканальної системи L дорівнює середній швидкості надходження заявок, що ділиться на різницю між середньою швидкістю обслуговування і швидкістю надходження заявок:

• при Гаусовому розподілі L = ;

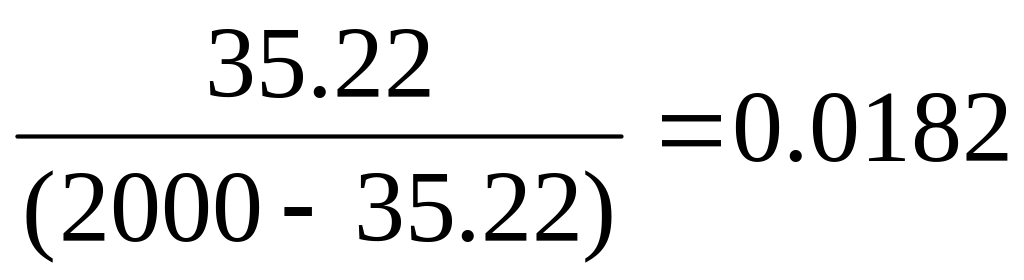• при нормальному розподілі L = .

Таким чином, в буфері маршрутизатора і лінії зв'язку у будь-який момент знаходиться трохи більше (0.36 – 1.82)% одного кадру. Щоб визначити середнє число об'єктів в черзі (L_q), перемножимо ступінь використання обслуговуючого пристрою (P) на число об'єктів в системі (L):

• при Гаусовому розподілі L_q = 0.0176*0.0182 = 0.00032;

• при нормальному розподілі L_q = 0.0036* 0.0036= 0.000012.

Розрахуємо середній час знаходження об'єкту в системі (t_ω) і середній час очікування в черзі (t_ωq). Середній час знаходження в системі є величиною, зворотною різниці між швидкістю обслуговування і швидкістю надходження заявок. Підставивши числа з нашого прикладу, знайдемо, що в даному випадку кожен кадр проводить в системі в середньому:

• при розподілі Гауса t_ω = сек;

• при нормальному розподілі t_ω = сек.

Черги в системі характеризуються ще часом очікування t_ωq, яке

рівне t_ωq = t_ω * P. Таким чином, для нашої мережі:

• при Гаусовому розподілі t_ωq = 0.000518 * 0.0176= 0.00000911 сек;

• при нормальному розподілі t_ωq = 0.000501 *0.0036 = 0.0000018 сек. [2]