5.4 Алгоритм шифрування aes

Advanced Encryption Standard (AES), також відомий, як Rijndael - симетричний алгоритм блокового шифрування (розмір блоку 128 біт, ключ 128/192/256 біт), фіналіст конкурсу AES і прийнятий як американський стандарт шифрування урядом США. Вибір був зроблений з розрахунком на повсюдне використання і активний аналіз алгоритму, як це було з його попередником, DES. За станом на 2006 рік AES є одним з найпоширеніших алгоритмів симетричного шифрування.

Цей алгоритм є симетричним блоковим шифром, який працює з блоками даних завдовжки 128 біт і використовує ключі завдовжки 128, 192 і 256 біт (версії AES-28; AES-192 і AES-256). Сам алгоритм може працювати і з іншими довжинами блоків даних і ключів, але ця можливість до стандарту не увійшла.

Біти даних нумеруються з нуля, починаючи із старших. У AES основним є поліноміальне представленням кодів. Так байт {01100011} слід представляти як: x6 +x5 + x + 1.

Алгоритм AES проводить операції над двовимірними масивами байт, що іменуються структурами (state). Структура складається з 4 рядів по Nb байт. Nb рівне довжині блоку, що ділиться на 32 (у даному стандарті Nb=4). Це дозволяє позначати структуру як sr,c або s[r,c], де 0<=r<4 і 0<=с<4..

Вхідний код (in), який є послідовністю 16 байт можна представити як: s[r,c] =in[r +4c].

При реалізації алгоритму AES використовуються операції складання байт (по модулю 2 = XOR) і множення. У алгоритмі AES при множенні байтів використовується багаточлен, що не приводиться: m(x)= x8 + x4 + x3 + x + 1. Обчислення твору М байтів {b1} на {b2} тут виконується згідно наступногоу алгоритму: M=[{b1}E{b2}] mod m(x).

В цьому випадку зворотна величина байта рівна: {b}-1 ={b} mod m(x)

для множення півбайтів (коди завдовжки 4 біта) використовується поліном, що не приводиться: m2(x) = x4 + 1.

Обчислення твору М півбайтів {a} на {b} тут виконується таким чином:

M=[{a}F{b}] mod m2(x), де M є півбайтом d. Операцію множення півбайтів {a} на {b} можна записати в матричному вигляді:

Як було сказано вище довжини ключів Nk (довжина, виміряна в 32 бітових словах) можуть приймати значення 4, 6 або 8 (для AES-128, -192 і -256, відповідно). Число ітерацій Nr (round), що реалізовуються в алгоритмі AES, складає відповідно 10, 12 і 14.

На кожному раунді алгоритму (число раундів залежить від довжини ключа) виконуються 4 дії (рис. 12):

1. Операція SubBytes, являє собою табличну заміну кожного байта масиву даних згідно наступній таблиці (табл. 6, рис. 13).

Замість даної табличної заміни можна виконати еквівалентну їй комбінацію двох операцій:

1.1. Обчислення мультиплікативної зворотної величини від вхідного значення в кінцевому полі GF(28); зворотною величиною від 0 є 0.

1.2. Вихідне значення b обчислюється таким чином:

b_i = a_iAa_{i + 4 mod 8} Aa_{i+5 mod 8} Aa_{i+6 mod 8} Aa_{i+7 mod 8} Ac_i , де n_i позначає i-й біт величини n, а - результат попередньої операції,

c - шіснадцяткова константа 63.

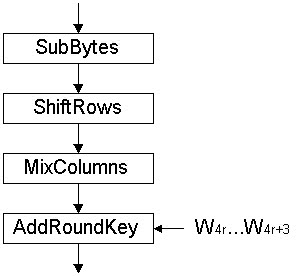
Рис. 12 Раунд алгоритму

Таблиця 6 - Таблиця замін операції SubBytes

Таблиця міняє вхідне значення 0 на 63 (шіснадцяткове значення), 1 - на 7C, 2 - на 77 і так далі.

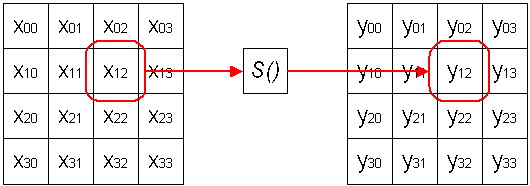
Рис. 13 Операція SubBytes

2. ShiftRows - циклічне зрушення управо кожного рядка матриці на певне число байт, залежне від номера рядка і розміру блоку. Для довжини блоків від 128 до 196 біт перший рядок не зрушується, другий рядок зрушується на 1 байт, третя на 2, четверта на 3. Для довжини блоку 256 біт третій рядок зрушується на 3 байти, четверта на 4 байти (рис. 14);

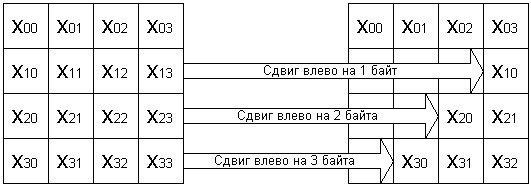
Рис. 14 Операція ShiftRows

3. Операція MixColumns. Виконує множення кожного стовпця масиву даних (рис. 15), який розглядається як поліном в кінцевому полі GF(2⁸), на фіксований поліном а(x): а(x)= 3x³ + x² + x + 2. Множення виконується по модулю x⁴ + 1.

4. Операція AddRoundKey виконує накладення на масив даних матеріалу ключа. А саме, на i-й стовпець масиву даних (i = 0...3) побітовою логічною операцією «исключающее ИЛИ» (XOR) накладається певне слово розширеного ключа W_4r+i, де r - номер поточного раунду алгоритму, починаючи з 1. Операція AddRoundKey представлена на рис. 16. Кількість раундів алгоритму R залежить від розміру ключа таким чином (табл. 7):

Таблиця 7 – Кількість раундів алгоритму R

Перед першим раундом алгоритму виконується попереднє накладання матеріалу ключа за допомогою операції AddRoundKey, яка виконує накладення на відкритий текст перших чотирьох слів розширеного ключа W₀…W₃. Останній же раунд відрізняється від попередніх тим, що в ньому не виконується операція MixColumns.

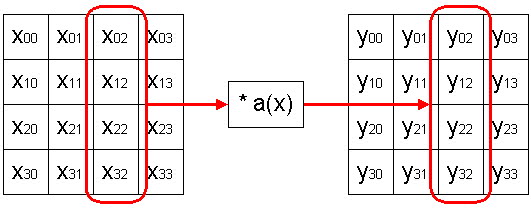
Рис. 15 Операція MixColumns

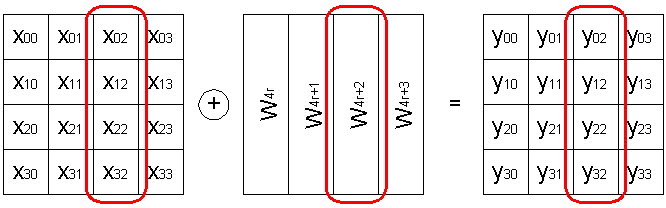
Рис. 16 Операція AddRoundKey

AES використовує ключі шифрування трьох фіксованих розмірів: 128, 192, і 256 біт. Залежно від розміру ключа, конкретний варіант алгоритму AES може позначатися як AES-128, AES-192 і AES-256 відповідно.

Розшифрування виконується застосуванням зворотних операцій в зворотній послідовності. Відповідно, перед першим раундом розшифрування виконується операція AddRoundKey (яка є зворотною самій собі), що виконує накладення на зашифрований текст чотирьох останніх слів розширеного ключа, тобто W_4R…W_4R+3.

Потім виконується R раундів розшифровування, кожний з яких виконує наступні перетворення (рис. 17):

Рис. 17 Раунд дешифрування

1. Операція InvShiftRows виконує циклічне зрушення управо трьох останніх рядків масиву даних на ту ж кількість байт, на яке виконувалося зрушення операцією ShiftRows при зашифровуванні.

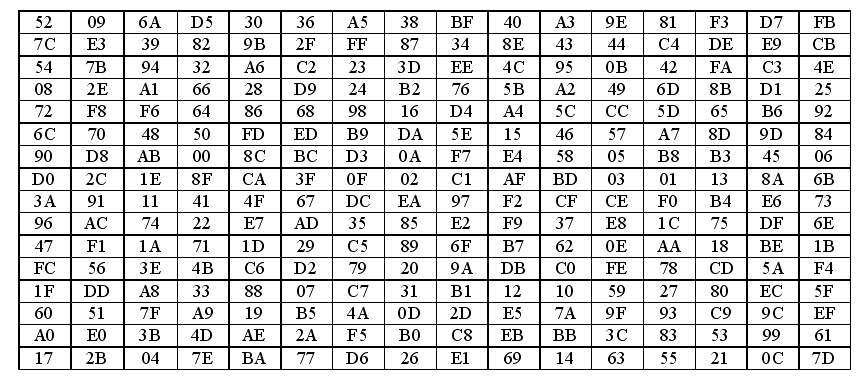
2. Операція InvSubBytes виконує побайтно зворотну табличну заміну, яка визначена наступною таблицею (табл.8). Дану табличну заміну можна виконати, застосувавши до вхідного байта перетворення, зворотне операції 1.2 (див. опис операції SubBytes), після чого обчислити мультиплікативну зворотну величину від результату попередньої операції в кінцевому полі GF(2⁸).

3. Операція AddRoundKey, як і при зашифрованії, виконує накладеання на оброблювані дані чотирьох слів розширеного ключа W_4r…W_4r+3. Проте, нумерація раундів r при розшифруванні проводиться у зворотний бік - від R-1 до 0.

Таблиця 8 - Таблиця заміни операції InvSubBytes

4. Операція InvMixColumns виконує множення кожного стовпця масиву даних аналогічно прямій операції MixColumns, проте, множення проводиться на поліном a^-1(x), визначений таким чином: a^-1(x) = Bx³ + Dx² + 9x + E. Аналогічно зашифровуванню, останній раунд розшифрування не містить операцію InvMixColumns. [3]