
- •Розділ 1 Поняття про інверсну населеність та енергетичні Рівні
- •1.1 Аналіз механізму утворення інверсних населеностей
- •1.2 Схема енергетичних рівнів рубінового лазера
- •Розділ 2 Режим модульваної добротності. Розрахунок енергетичних характеристик
- •2.1 Робота лазера в режимі модульваної добротності
- •2.1 Розрахунок енергетичних характеристик рубінового лазера
Міністерство освіти і науки, молоді та спорту України
Конотопський інститут СумДУ
Факультет денної форми навчання
КУРСОВА РОБОТА
з дисципліни: «Квантова електроніка»
на тему: Розрахунок енергетичних характеристик твердотілого лазера, який працює в режимі модульованої добротності
Виконав:
студент групи ЕП-91к Котлубаєв М.Є.
Перевірив:
викладач Бурик І.П.
Конотоп 2012
ЗМІСТ
Вступ…………………………………………………………………………. |
3 |
|||
РОЗДІЛ 1. |
Поняття про інверсну населеність та енергетичні Рівні |
|
||
1.1 |
Аналіз механізму утворення інверсних населеностей |
5 |
||
1.2 |
Схема енергетичних рівнів рубінового лазера |
9 |
||
Розділ 2. |
Режим модульваної добротності. Розрахунок енергетичних характеристик |
|
||
2.1 |
Робота лазера в режимі модульваної добротності |
21 |
||
2.2 |
Розрахунок енергетичних характеристик рубінового лазера |
22 |
||
Висновки……………………………………………………………………. |
29 |
|||
Список використаної літератури…………..…………………….. |
30 |
|||
Вступ
Перший рубіновий лазер з’явився в 1960 році. Його винахідником був Т. Нейман. Лазер працював на твердотільному рубіновому генераторі. Створенню першого лазера передували фундаментальні винаходи радянських і зарубіжних учених.
В наш час створені лазери з виходною енергією до 5000 Дж і імпульсом понад 20 ГВт, що не є граничним значенням. Такі великі потужності необхідні для різних практичних і наукових цілей, і можуть бути досягнуті тільки при імпульсній роботі лазера, при визначеній форміі тривалості випромінюючого імпульсу.
Рубін — це тверда кристалічна речовина, яка використовується в рубіновому лезері. Основою його є корунд — діелектричний кристал окислу алюмінію. Рубіном він стає тоді, коли невелику частину атомів А1 в цьому кристалі замінюють іони хрому Сг. Вміст атомів Сг в кристалі невеликий (0,05%). В рубіні, який використовується для лазерів, на кожний см3 кристала доводиться 1019 атомів Сг. Це складає приблизно одну десятитисячну від повного числа атомів. І проте саме з введенням атомів Сг кристал приймає характерний для рубіна червоний колір. Колір кристала обумовлений розташуванням енергетичних рівнів атомів Сг в рубіні.
Сьогодні лазери широко використовуються в різних областях людської діяльності. Вони міцно увійшли до побуту у вигляді лазерних дисків, указок, принтерів і т.д. У техніці зв'язку без лазерів неможливо представити сучасні волоконно-оптичні і атмосферні лінії зв'язку, оптичні підсилювачі, оптичний зв'язок між космічними апаратами. У технології могутні лазери використовуються для прецизійної обробки матеріалів і зміцнення поверхонь. У екології вони забезпечують високоточний моніторинг навколишнього середовища. У медицині лазери замінюють скальпель при якнайтонших хірургічних операціях, а також широко використовуються в діагностиці і лікуванні. У багатьох оборонних системах лазери також займають центральне місце.
Розділ 1 Поняття про інверсну населеність та енергетичні Рівні
1.1 Аналіз механізму утворення інверсних населеностей
Розглянемо більш
докладно схему рівнів, представлену на
рисунку 1.1
Будемо вважати, що кратність виродження
рівнів 1, 2 і 3 рівні:![]() .
Крім того, нехай все
.
Крім того, нехай все ![]() (оптичний діапазон). Рівні 1 і 2 зв’язані
випромінюванням, індукованим переходом
з імовірністю
(оптичний діапазон). Рівні 1 і 2 зв’язані
випромінюванням, індукованим переходом
з імовірністю ![]() .
.
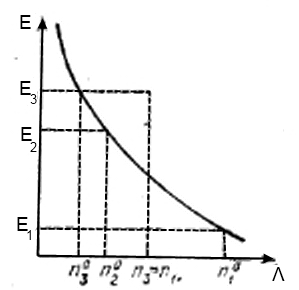
Рисунок 1.1 – До ідеї методу допоміжного випромінювання накачки в багаторівневих системах. Населеності рівней Е3 і Е1 зрівняні при насиченні випромінювання переходу 1→3, на переході 3→2 виникла інверсія [1]
Розпад рівня 2 проходить по двом каналам (2→1 і 2→3) з ймовірностями ω21 і ω23 відповідно. Рівень 3 розпадається з ймовірністю ω31. Зважаючи на умову термічним заселенням рівнів 2 і 3 можна знехтувати, поклав релаксаційні ймовірності ω12, ω13, ω32, які рівні нулю.
Тоді швидкісні рівняння для населеностей рівнів 1, 2 і 3 відповідно записуються у вигляді:
![]()
![]() (1.1)
(1.1)
![]()
де N – густина
частин,
які володіють рівнями енергії,
представленими на рисунку 1.2.
В стаціонарному режимі, коли всі
![]() для різниці населеностей n3
– n1
легко
отримати:
для різниці населеностей n3
– n1
легко
отримати:
![]() (1.2)
(1.2)
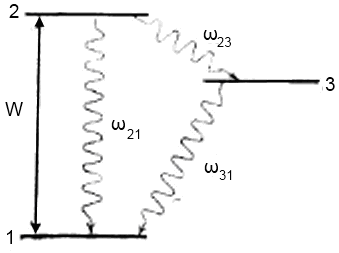
Рисунок 1.2 – До визначення умов досягнення інверсії в трьохрівневій системі оптичного діапазона. Прийнято традиційне позначення номерів рівнів[1]
Умовою інверсії на переході 3→1 є позитивність чисельника в дробі 15, що досягається при:
![]() (1.3)
(1.3)
Виконання нерівності (1.3) можливе лише при
![]() (1.4)
(1.4)
Сенс останньої умови зрозумілий: в процесі безвимпромінювальних переходів верхній рівень повинен населятись швидше, ніж спустошуватись. Забігаючи наперед, слід сказати, що схема рівнів на рисунку 3 і швидкісні рівняння (1.1) відповідають рубіновому лазеру. Для рубіну рівень 3 є метастабільним, а для ймовірностей безвипромінювальних переходів ω23, ω31, ω21 виконується нерівність:
![]() (1.5)
(1.5)
Тоді умова інверсії набуває вигляд:
![]() (1.6)
(1.6)
Сенс цієї умови простий: якщо з верхнього безпосередньо накачуваного рівня частинки поступають на метастабільний рівень значно швидше, ніж стікають з нього, то інверсія створюється і утримується, якщо верхній рівень накачується швидше, ніж спустошується метастабільний рівень.
В цих умовах різниця населеностей складає
![]() (1.7)
(1.7)
і при W→∞ прямує до N, що звичайно, як правило, не реалізується.
Так як в розглядуваній трьохрівневій схемі інверсія створюється по відношенню до основного стану, то виникає вона не одразу після включення накачки. Частинка повинні накопичитись на метастабільному рівні під дією накачки протягом деякого скінченного часу τ. Для відповіді на питання про те, коли різниця n3 – n1 стане додатною, необхідно розглянути перехідні процеси, тобто розв’язати систему диференціальних рівнянь (1.1). Не розглядаючи загальний розв’язок, звернемося до рубінового лазера. В цьому випадку ймовірність безвипромінювального переходу ω23 є найбільшою із усіх швидкостей процесів, які визначають розподіл частинок по рівням 1, 2 і 3. Для рубіна не тільки виконується умова (6), але і при всіх інтенсивностях накачки:
![]() (1.8)
(1.8)
Це означає, що на резонансному рівні 2 частинки не накопичуються, іх там немає, так як вони зразу ж передаються на метастабільний рівень 3. В лазерному циклі накачки, який показаний на рисунку3, рівень 2 грає роль посередника, який передає енергію збудження верхньому лазерному рівню 3, подібно тому я це робить азот в СО2 – лазері. Тоді, вважаючи n2 = 0, і отже, враховуючи n3 = N - n1, ми зводимо систему (1.1) до одного рівняння першого порядку:
![]() (1.9)
(1.9)
Звідси
легко
виходить
рівняння для інверсії ![]() :
:
![]() (1.10)
(1.10)
При початковій умові x(0) = -N розв’язання цього рівняння має вигляд:
![]() (1.11)
(1.11)
що при t→∞, як і слід було очікувати, переходить в (1.7). При запису в подальшомуаналізі віразу (11) передбачається, що накачка вмикається в момент
t = 0 і залишається в подальшому незмінною. Тимчасовий хід відносної інверсії x/N показаний на рисунку 1.3.
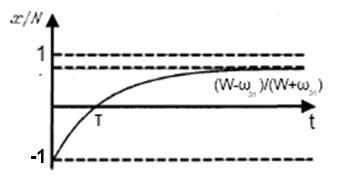
Рисунок 1.3 – Часовий хід відносної інверсії в трьохрівневій схемі при швидкості накачки W, яка вмикається в момент t = 0 [3]
Час просвітлення робочого переходу τ легко визначається з (1.11) прирівнюванням x(t) до нуля:
![]() (1.12)
(1.12)
В
практично недосяжному випадку максимальної
інверсії ![]() добуток Wτ
постійний:
добуток Wτ
постійний:
![]() (1.13)
(1.13)
Так як ймовірність індукованих переходів накачки пропорційна інтенсивності накачки, то цей добуток визначає максимальну енергію, необхідну для приведення системи в стан с від’ємним поглинанням. В загальному випадку:
![]() (1.14)
(1.14)
Сталість добутку Wτ пр великих інтенсивностях накачки, коли впливов всіх релаксаційних процесів можна знехтувати, має простий фізичний сенс: цей добуток пропорційний енергії, яка необхідна для переводу усіх частинок із основного стану на верхній лазерний рівень (формула (1.7) і рис. 3).
Доцільно підкреслити ще раз, що необхідність попередньої затрати енергії при створенні інверсії населеностей матастабільного рівня по відношенню до основного стану в оптичній трьохрівневій системі обумовлена тим, що доводиться переводити з рівня 1 через рівень 2 на рівень 3 принаймні половину всіх частинок. Інверсія в трьохрівневій системі створюється по відношенню до добре заселеному основному стану. Тому представляють великий інтерес схеми, в яких оптична накачка створює інверсію по відношенню до незачеленому термічному рівню, як це відбувається наприклад в газових лазерах при збудженні електронним ударом. Це може бути зроблено за допомогою чотирьох рівневої системи.
Також механізм утворення інверсних населеностей в рубіновому лазері можна пояснити за схемою на рисунку 1.4.
Інверсія виникає
тоді, коли верхній рівень заселений
більше чим нижній, тобто коли N3
- N2
>0. Ця нерівність виконується за умови
![]() .
.
У виді того, що![]() ,
умова існування негативної температури
між рівнями 2 і 3 записуються як
,
умова існування негативної температури
між рівнями 2 і 3 записуються як![]() .
.
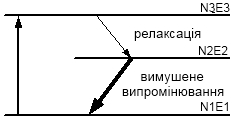
Рисунок 1.4 – Механізм створення інверсії населеності в трьохрівневих схемах [3]
Фізичний зміст цієї умови полягає в тому, що час життя часток на рівні 3 повинне бути якнайбільше для того, щоб на ньому накопичувалися частки, а час життя на рівні 2 – як можна меншим. Тільки в цьому випадку на частоті 32 при переході часток з рівня 3 на рівень 2.
Залежність населеностей рівнів від щільності (інтенсивності) збуджуючого випромінювання накачки можна показати на рисунку 1.5.
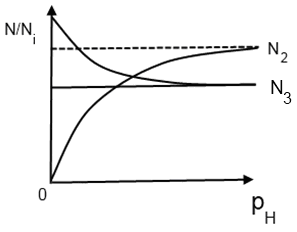
Рисунок 1.5 – Залежність населеностей рівнів від щільності (інтенсивності) збуджуючого випромінювання накачки [5]
При виборі трьохрівневій квантової системи, в якій повинна створитися інверсія, по першому типу час життя на допоміжному верхньому рівні повинен бути значно менше ніж час життя на рівні, щодо якого створюється інверсна населеність. Так, у трьохрівневій системі час життя на рівні 3 повинне бути порядку 32 10-7 …10-8 с, на рівні 2 – 21 10-3. Важливо, щоб верхній допоміжний рівень 3 був як можна ширше, тому що для накачування використається як правило газорозрядні лампи із широким спектром випромінювання.
