Добавил:

Studfiles2 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

Математический анализ

Файл:

Математический анализ. Конспект лекций / T2_Lection_Full

.pdf

Скачиваний:

251

Добавлен:

01.05.2014

Размер:

479.92 Кб

Скачать

☆

1 / 61 2 3 4 5 6 > Следующая >>>

Математический анализ. Конспект лекций.
Оглавление
Определенный интеграл и его приложения.....................................................................................................	3
Интеграл Римана .........................................................................................................................................................	3
Неравенство Коши-Буняковского......................................................................................................................	4
Свойства интеграла с переменным верхним пределом. Формула Ньютона-Лейбница.......	4
Формула замены переменных в определенном интеграле .................................................................	5
Интегрирование по частям в определенном интеграле........................................................................	5
Теорема о среднем для определенных интегралов .................................................................................	5
Примеры вычисления определенных интегралов ...................................................................................	6
Об интегрировании периодических функций.............................................................................................	6
Формула Тейлора с остаточным членом в интегральной форме.....................................................	7
Несобственные интегралы ....................................................................................................................................	7
Простейшие несобственные интегралы ........................................................................................................	8
Критерии сходимости несобственных интегралов..................................................................................	8
Примеры на сходимость несобственных интегралов.............................................................................	9
Признак Дирихле условной сходимости несобственного интеграла..........................................	10
Примеры на признак Дирихле ..........................................................................................................................	11
Вычисление несобственных интегралов....................................................................................................	11
Приложения определенного интеграла......................................................................................................	12
Простейшие методы численного интегрирования...............................................................................	17
Операционное исчисление.......................................................................................................................................	20
Преобразование Лапласа и его свойства.....................................................................................................	20
Изображения некоторых элементарных функций................................................................................	22
Восстановление оригинала по изображению...........................................................................................	22
Обыкновенные дифференциальные уравнения..........................................................................................	23
Основные определения и примеры................................................................................................................	23
Задача Коши................................................................................................................................................................	24
Метод Эйлера решения ДУ..................................................................................................................................	24
Линейные ДУ и преобразование Лапласа...................................................................................................	25
Классификация ДУ первого порядка.............................................................................................................	26
Теорема существования и единственности решения задачи Коши для ДУ первого
порядка ..........................................................................................................................................................................	29
Об уравнениях высшего порядка ....................................................................................................................	30
Особые решения ДУ первого порядка...........................................................................................................	30
Числовые ряды...............................................................................................................................................................	32
Общие понятия и определения ........................................................................................................................	32
Условия сходимости ряда....................................................................................................................................	32
Вычисление сумм рядов.......................................................................................................................................	33

Условия сходимости рядов для положительных общих членов....................................................	34
Перестановка слагаемых в рядах.....................................................................................................................	36
Признаки сходимости (условной) знакопеременных рядов............................................................	37
Примеры на сходимость рядов.........................................................................................................................	37
Признак Абеля-Дирихле.......................................................................................................................................	38
Функциональные последовательности и ряды ...........................................................................................	39
Основные понятия и определения .................................................................................................................	39
Теорема Вейерштрасса о мажорируемой сходимости.........................................................................	39
Теорема Вейерштрасса о непрерывности предельной функции...................................................	40
Интегрирование и дифференцирование функциональных рядов...............................................	40
Степенные ряды........................................................................................................................................................	41
Дифференциальное исчисление функций нескольких переменных ...............................................	44
Основные понятия и определения .................................................................................................................	44
Сходимость...................................................................................................................................................................	44
Непрерывность..........................................................................................................................................................	45
Частная производная.............................................................................................................................................	45
Производная по направлению..........................................................................................................................	46
Дифференцируемость. Дифференциал........................................................................................................	47
Геометрическая интерпретация дифференциала. Касательная плоскость. Нормаль.......	48
Экстремальные свойства градиента..............................................................................................................	49
Инвариантность формы первого дифференциала ................................................................................	49
Формула Тейлора .....................................................................................................................................................	49
Исследование функций на экстремумы.......................................................................................................	50
Нахождение наибольшего и наименьшего значения функции......................................................	52
Условный экстремум..............................................................................................................................................	52
Экзаменационные вопросы.....................................................................................................................................	55

Определенный интеграл и его приложения

Интеграл Римана

	f(x)
ξ1
	ξn
ξ2
	x
0 a = a0 a1 a2	an–1 an = b

Интегрируемая функция f(x) ограничена на интервале [a, b]:

Рассмотрим некоторое разбиение P интервала [a,b] (см. рис), содержащее a = a, a , .. a = b.

0 1 n

Для разбиений вводятся отношения частичного порядка. Например, (P1 мельче P2): P1 получается из P2 путем деления на более мелкие части и.т.п. Разумеется, не все разбиения сравнимы, а только те, которые содержат хотя бы одно общее ai, кроме концов интервала [a,b].

Для данного разбиения введем верхнюю U(P, f) и нижнюю L(P,f) интегральные суммы
(Дарбу) следующим образом:					'
(Дарбу) следующим образом:

			$ % &
	!"#				(
)	*+,	$ -			'
)	*+,	$ -			& )
	!"#
С измельчением разбиения P верхние суммы				уменьшаются, а нижние – увеличиваются.
С измельчением разбиения P верхние суммы					(
Введем тогда верхний и нижний интегралы
. / *+, % . / -
	0				0

Если нижний интеграл равен верхнему, говорят что функция f(x) интегрируема на

интервале [a,b] и существует интеграл Римана1 (определенный интеграл)

. /

Введем (для удобства) просто интегральную сумму, находящуюся между U и L и

являющуюся, соответственно, аппроксимацией' определенного интеграла:

2 & 3 4 3

(

Очевидно, определенный интеграл является пределом интегральных сумм.

С использованием S за счет линейности суммы можно легко доказать, что интеграл суммы равен сумме интегралов, а константа выносится за знак интегрирования (линейность операции интегрирования) и т.д.

Неравенство Коши-Буняковского

1) Для чисел

5 6 7 8 9

& 5

Доказательство:'

(

>'(' A >'('

>(' 5

7 &

=>( 5

(

;=>(

>(' 5

=>(

>( 5

7 C

=>'( >(' 5

& 5

(

2) Для интегралов

. D / :. / . D /

Доказательство: рассмотрим интегральную сумму

2 & 3 D 3

& 3 E D 3 E :& 3 & D 3

(

Устремим

и получим искомое соотношение.

FGH I 7

Свойства интеграла с переменным верхним пределом. Формула Ньютона-Лейбница

Пусть функция (x) интегрируема на [a, b], и некоторая точка											. Определим
интеграл с переменнымf				"				M		J
интеграл с переменнымf				верхним пределом			как функцию			J
		K . L /L N J $ K .							L /L 4 J
	F' x	f(x).			1M	1M		"
Очевидно,	( ) =		ВведемM
			O . L /L . L /L . L /L J
OP 7 F(x), таким1					"						f x
					образом, однаM		из первообразныхM				( ). С другой стороны,
				. / KJ			KJ	OJ OJ

где Φ(x) – любая из первообразных f(x). Полученная нами формула носит название формулы Ньютона-Лейбница. Согласно ей, приращение любой первообразной равно определенному интегралу. Формула устанавливает связь между определенным и неопределенным

интегралами; она часто (но не всегда) используется для вычисления значения определенного интеграла. Например, нельзя с ее помощью посчитать интеграл нечетной

функции f(x)
	. /

Формула замены переменных в определенном интеграле

Пусть имеются функции f(x) – непрерывная на интервале [a, b] и φ(t) – дифференцируемая
на [α, β], причем φ(α) = a, φ(β) = b.UТогда справедлива1следующая формула:
				. QR L SRT L /L . /
называемая	формулой замены			переменных.
W	формулой замены			V	1			1
W		U		W	1		U	1
Вывод ее опирается на такую же формулу для неопределенного интеграла:
. QR L SRT L /LX		V	. / X		R L Y .			QR L SRT L /L . /
		V					V
Интегрирование по частям в определенном интеграле
	1					1	1
Для определенного интеграла справеливо соотношение
					W		.	T D /
	. DT / D						.	T D /

называемое формулой интегрирования по частям.

1	Q D SP
Доказательство:
.Q D SP/
	1
	. T D / A

T D A DT
1	1
. T D / A . DT /
1		1
	W
. DT / D

Теорема о среднем для определенных интегралов

Пусть функция f(x) – непрерывная1 на интервале [a, b]. Тогда можно записать

. / Z Z

Это утверждение носит название теоремы о среднем для интегралов.

Доказательство: Применим обычную теорему о среднем и формулу Ньютона-Лейбница.

O ." L /L .1 / O O OT Z

Примеры вычисления определенных интегралов

[

*+ L

[

L /L

C . E

/ ]^ L /L

\ . E

*+ L ]^ L /L

. ]^

[

C A ]^ BL

` C

[

A W *+ BLX

` f+ B

` C

B f+ C A

XJ a

B . Gc]de / . C A / A Gc]de

. h / h h A C C

g . h / h

a . *+ h"/ i

[

i . *+ / h

*+ h

]^ / h

[

. ]^ / h

[

]^ h

J . h

[

A C i

. *+ h"/ h

Bi h

[

A C

[

A Ck

B jh

Об интегрировании периодических функций

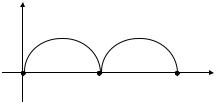
Пусть функция f(x) имеет период T. Тогда

/ . /

так:

Графически это можно изобразить

f(x)

…

Формальное доказательство:

. / L A n . L A n /L . L /L . L /L

J m

lmJ

. /

. / A . / A . / . /

Формула Тейлора с остаточным членом в интегральной форме

Формула Тейлора:

' o J

A ro

o(J

s J o

ol t J ol

и в форме Лагранжа:

в форме Пеано:

где остаточный член rk(x) можно записатьpq

Пусть функция

f x

PLp A C q

( ) имеет ( +1) непрерывную производную, тогда

" P

L /L

u w L L

A .

A . v L /w L

A v L w L "

u /vL PPL/L u

/w L L /L

ol L L o

. w L /v L x J A

J J A x A .

p A C q

где

" ol L L o

остаточный член

ro ".M

p A C q

Несобственные интегралы

– это интегралы от функций с особенностями, не позволяющими воспользоваться формулой Ньютона-Лейбница непосредственно.

Пусть задана функция f(x), которую требуется проинтегрировать на интервале [a, b]. Возможно несколько вариантов:

1) Особенность в b.

f(x)	a	1		1P	b
y	a	. / f*F . /			b
		. / f*F . /
			1PI1

2) Особенность в a.

y		a			b
		a			b
		1		1
	f(x)	1		1
	f(x)		. / f*F . /
			. / f*F . /
				PI P

0	a	a'	b	x	7

3) Особенность в +∞.

y		a
	f(x)	a	ly		1
	f(x)

			. /	f*F . /
				1Ily

0	a	b	x
0	a	b	1
4) Особенность в –∞.			1
		. /	f*F . /
		y	1I y

5) Несколько особенностей.

Интеграл разбивается на несколько подинтегралов так, чтобы на каждом интервале интегрирования была только одна особенность. Такой интеграл сходится (предел равен конечному числу), если сходятся все подинтегралы.

Простейшие несобственные интегралы

/				W C					V
C . V				C z						XJ z { C \|}~•€•\|‚ ƒ„€ z N C
J		/				W
z C .						W			J	„…\|}~•€•\|‚
z C .					f+					„…\|}~•€•\|‚
y		J		W C			VXy \|}~•€•\|‚ ƒ„€ z N C
B .	/V			W C			VXy \|}~•€•\|‚ ƒ„€ z N C
				C z
y	/V			W C			VXy „…\|}~•€•\|‚ z
g .	/V			W C			VXy „…\|}~•€•\|‚ z
J				C z						J
a . h					W					J
a . h		"	/ h							7 C C
y		"						" y
J
Критерии сходимости несобственных интегралов											1PP
			1							† ~\|~‡…‚ •~ˆ‰…	1PP
1) Критерий Коши										(хорош для теории, а не для практики).
			. / 4 † Š ‹ N 7 Œ J 4 J 4 J 4 P 4 PP 4 Y •. / • 4 ‹
											1P

Доказательство:

"
O . L /L I f*F O 4 J 4 4 P 4 PP 4 O T O TT ‹
	"I1	1PP

O T O TT . /

+∞

1 D / 1 /

. 4 † Y . 4 †

Ž /

сходится условно

Ž /

. Если сходится лишь

2) Интеграл

сходится абсолютно, если сходится

говорят,

что интеграл

Если интеграл сходится абсолютно, то он сходится:

. / 4 †

‹ N 7 Œ J N P PP N J

•. / • . / 4 ‹

•. / • 4 ‹

3) Пусть даны функции

, определенные на интервале [a, b].

Если интеграл от большей функции g(x) (мажоранты) сходится, то и интеграл от меньшей функции сходится:

Если интеграл от меньшей функции f(x) расходится, то и интеграл от большей функции

расходится:

. / † Y . D / †

Так получается за счет условия сходимости

1PP

4 P 4 PP 4

/ . D / 4 ‹J

Если существует предел1P

z N 7

f*F

расходятся"I1

одновременно:

то функции f(x) и g(x) сходятся или

4 Bz N N J

B D

D Bz

Примеры на сходимость несобственных интегралов

y *+

/ $ ‹ N 7 † 4

N J

C .

B B

J 1PP

1PP

/ ]^

]^ 1PP

1PP

•.

/ • •.

•

\1P

A . ]^

• T A •.

• T J

4 ‹ J N ‹

Покажем, что этот интеграл не сходится абсолютно:

•[

' [l •

/ †

. *+

/ & .

/ 6 & C

[

*+ / 6 tJ & C

6 tJ & .

[ '

'( 9

[ ' l•

y
B . + p h "/ \|}~•€•\|‚ ‘… \|ˆ’• + p h " h "
J		/			/
		/			/	I 7 „…\|}~•€•\|‚
g .	*+			“ .		I 7 „…\|}~•€•\|‚
J					J
		/			„…\|}~•€•\|‚ƒ~ •’• –’ƒ„€ˆ€—…•
a .		/			„…\|}~•€•\|‚ƒ~ •’• –’ƒ„€ˆ€—…•
	*+		”
Jy			”
˜ .		g A ˜ h "/					"
J							"	7
						f*F g A ˜ h		7	"
						"Iy		"	"	I 7 I †
						g A ˜ h " g A ˜ h h				I 7 I †
						"	N J
						g A ˜ h " h	N J

Признак Дирихле условной сходимости несобственного интеграла

Интеграл	1
	. R D / †
сходится, если выполнены два	следующих условия.
сходится, если выполнены два

1) Φ(x) – первообразная φ(x):	"
	O . R /
	O
Будем считать Φ(x) ограниченной функцией:

2) g(x) дифференцируема и монотонно убываетD ™к70:

Доказательство: Воспользуемся признаком Коши. b', b'' > b.

a	b'' b' b			1PP
				1PP
			1PP	•. R D / • 4 ‹
Запишем			1PP	1	1PP
			•. R D / • •. D /O •
				1PP
и воспользуемся формулой		интегрирования по частям. Получим
и воспользуемся формулой			1		1
			•	. O DT / A D O •
1PP			DO		D T A D TT B ‹
1PP				1PP	1PP
Рассмотрим две части суммы.				1P	šO D š / . DT / B ‹
• .	O DT / • .				šO D š / . DT / B ‹
1P				1P	1P

1 / 61 2 3 4 5 6 > Следующая >>>