Глава «Ряды Фурье» 1

§1 Постановка задачи приближения функций. Равномерное и среднеквадратическое приближение. 1

§2 Понятие о ряде Фурье. Коэффициенты Фурье. Многочлен наилучшего среднеквадратического приближения функции. 3

Свойства нормы 4

Глава «Ряды Фурье»

§1 Постановка задачи приближения функций. Равномерное и среднеквадратическое приближение.

Пусть на некотором множестве задана функция .

Приближением функции f называют ее замену на другую функцию g ,

(a) «более удобную» для целей исследования и (b) «достаточно близкую к f»

Прежде чем сформулировать математически постановку задачи приближения, необходимо решить, исходя из целей такого приближения, две «проблемы»:

1. Выбрать (задать) множество (класс) функций , в котором ищется приближение.

Например, пусть над функцией g необходимо выполнить некоторую операцию А , объект Аg существует, но алгоритм его отыскания не известен или слишком трудоемок (в том числе и технически). Тогда, естественно, приближение функции следует искать во множестве функций, операция А над которыми выполняется быстро и просто.

В инженерной практике: g(t) – сигнал на входе электронного устройства А, А[g(t)] – сигнал на выходе; известен алгоритм А[f] для гармонических сигналов. В качестве удобно использовать множество тригонометрических функций F={1, sin(kt), cos(kt); k=1,2,…}.

2. Выбрать (задать) “критерий отбора”, “меру близости”, “расстояние между f и g в D» 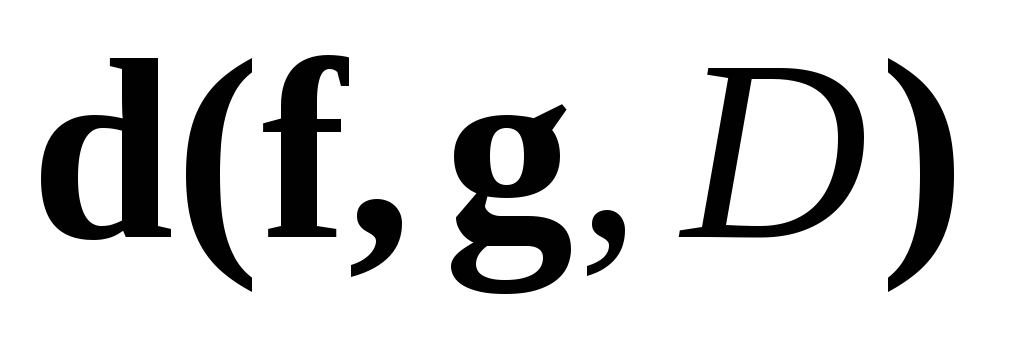После того как решены эти нематематические проблемы - (выбраны, заданы) 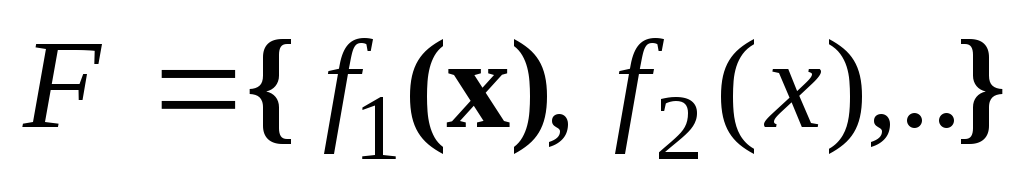, , 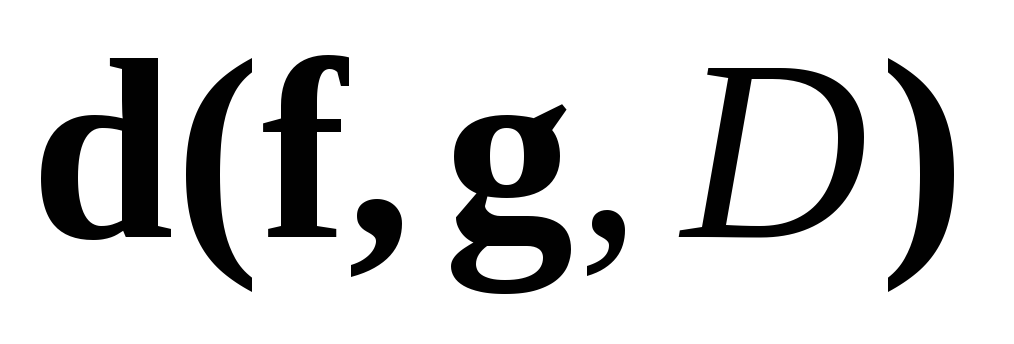математическая задача приближения формулируется так :

«В заданном классе функций найти «элемент наилучшего приближения» , «наиболее близкий» к f в соответствии с выбранным критерием ».

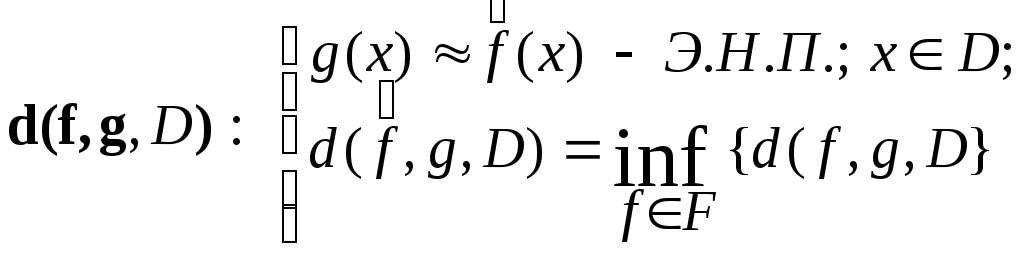Алгоритм решение поставленной задачи приближения:

1. Исследовать существование и единственность Э.Н.П.

2. Построить метод отыскания Э.Н.П.

3. Найти Э.Н.П. 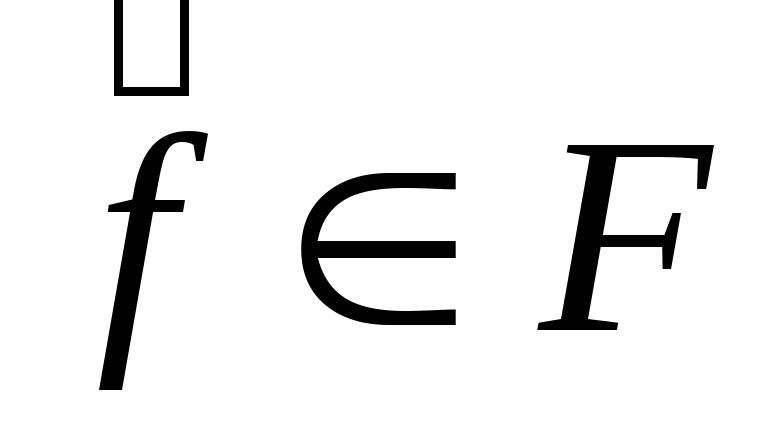и “вычислить” качество полученного приближения – .

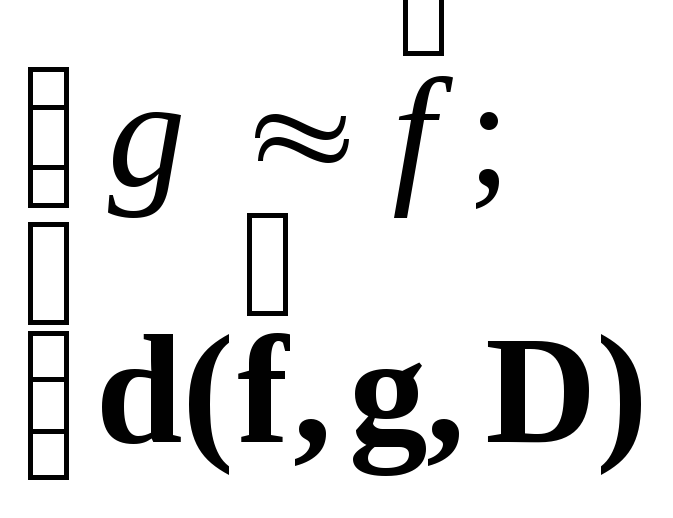Рассмотрим несколько примеров постановки и решения задачи приближения функций.

[I] В дифференциальном исчислении для целей локального исследования дифференцируемой функции g в окрестности точки дифференцируемости

1. приближение ищется во множестве полиномов степени ”n”

;

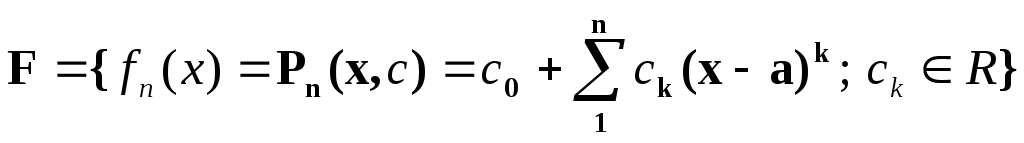2. в качестве критерия 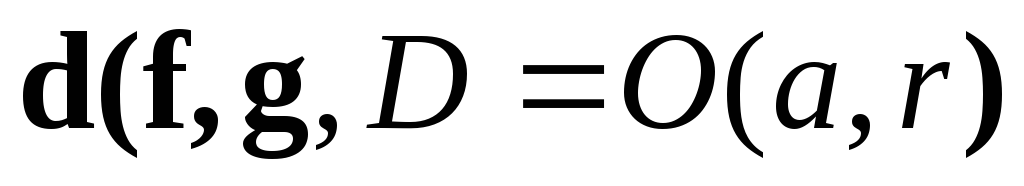используется скорость убывания остатка 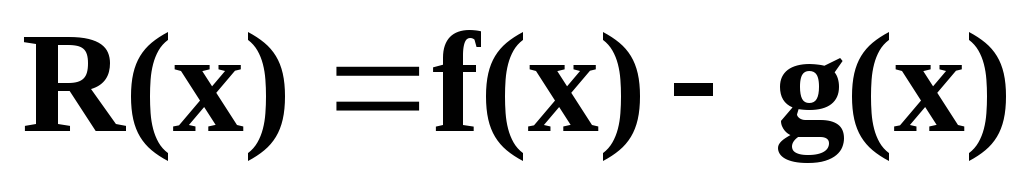по сравнению с функцие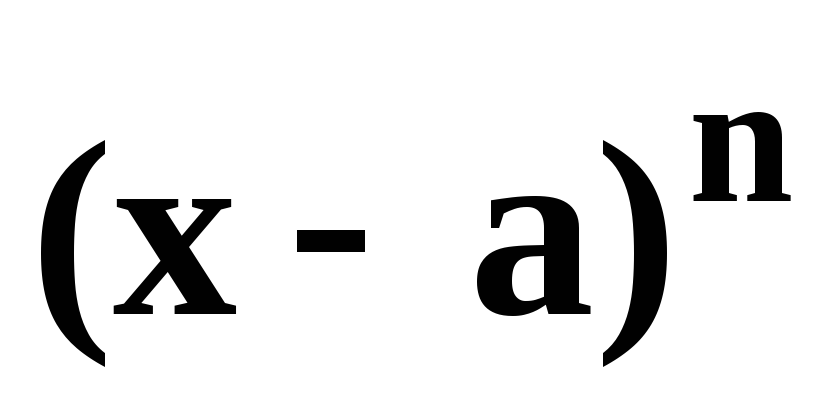й при .

 Известно, что полином наилучшего приближения существует, единственен и называется полиномом Тейлора

причем

[II]. В математике при решении задачи приближения функции g на конечном промежутке D=[a,b] в качестве «критерия отбора» – «расстояния от f до g» принимают неотрицательное число, называемое «нормой разности функций»

.

Элемент наилучшего приближения , соответствующий такому критерию, удовлетворяет соотношению

Существуют различные способы определения “нормы функции”, но все они должны удовлетворять условиям – аксиомам нормы:

а) Норма функции – неотрицательное число

б)

в) - норма суммы функций не больше суммы норм слагаемых.

Рассмотрим некоторые варианты введения нормы остатка R(x)=f(x)-g(x);

1. Равномерная норма для функций, непрерывных на промежутке:

2. Если функции f и g абсолютно интегрируемы на [a,b] ,

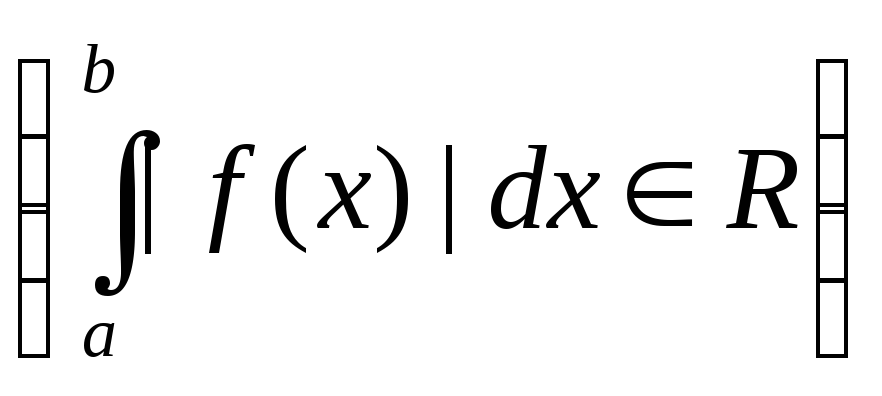- «расстояние» равно площади криволинейной трапеции

называется наилучшим приближением функции g «в среднем»;

2. Если функции f,g квадратично интегрируемы на [a,b] , вводится среднеквадратическая норма

Функция , минимизирующая эту норму, называется «наилучшим среднеквадратическим» приближением функции g на промежутке [a,b] (в заданном множестве(классе) функций) .

§2 Понятие о ряде Фурье. Коэффициенты Фурье. Многочлен наилучшего среднеквадратического приближения функции.

Пусть задана бесконечная система квадратично интегрируемых на конечном промежутке [a,b] функций F={f₁(x), f₂(x),..,f_k(x),…}, т.е. конечны интегралы

Введем для таких функций определения скалярного произведения, нормы и ортогональности функций.

1. Скалярным произведением функций 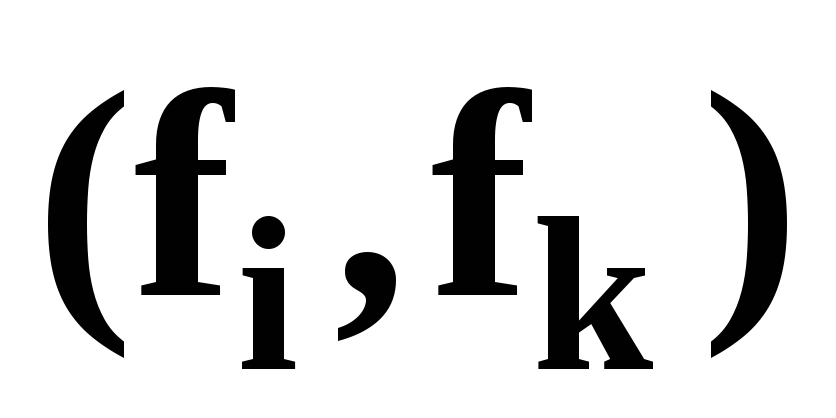называется вещественное число, равное интегралу от их произведения

Очевидные свойства С.П.

2. Нормой функции называется неотрицательное число, равное арифметическому значению квадратного корня из интеграла от квадрата функции :

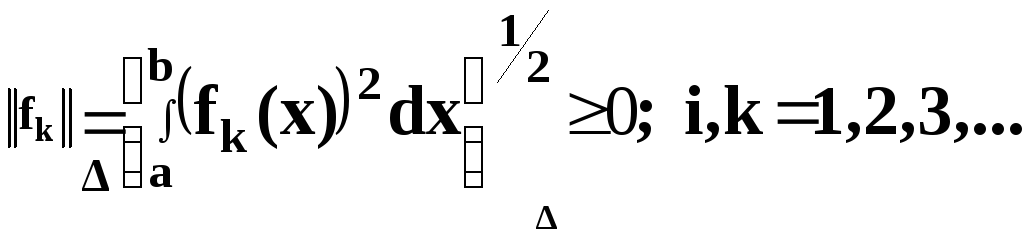
Свойства нормы

3. Две функции называются ортогональными на промежутке, если их скалярное произведение равно нулю. Множество F={f₁(x), f₂(x),..,f_k(x),…} попарно ортогональных функций называется ортогональным на промежутке.

Пример.

Множество тригонометрических функций , имеющих общий период , ортогонально на промежутке

Заметим, что для доказательства ортогональности множества необходимо вычислить шесть !! скалярных произведений

Например,

Пусть функция g(x) квадратично интегрируема и множество F={f₁(x), f₂(x),..,f_k(x),…} ортогонально на промежутке [a,b].

Рассмотрим бесконечный ряд и предположим, что

1. ряд сходится на промежутке, т.е. на [a,b] определена функция S(x) - сумма ряда

;

2. ряд почленно интегрируем на промежутке ;

3. имеет место равенство .

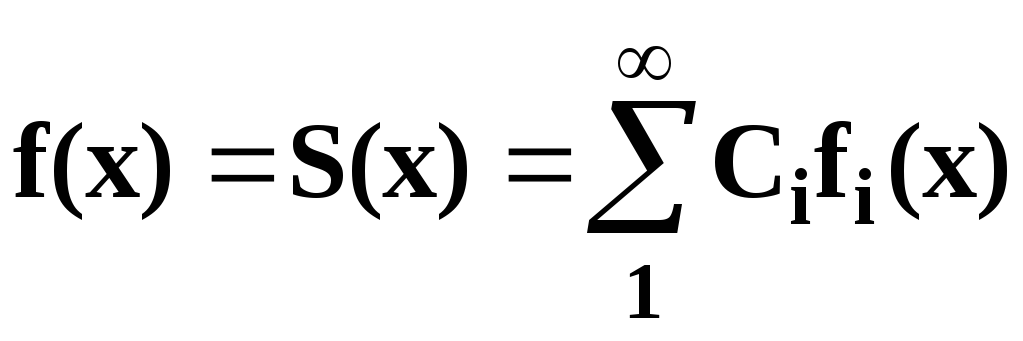Найдем коэффициенты последнего ряда. Для этого : (а) домножим равенство на функцию f_k(x) и (б) проинтегрируем по промежутку [a,b] :

Определение.

Равенство 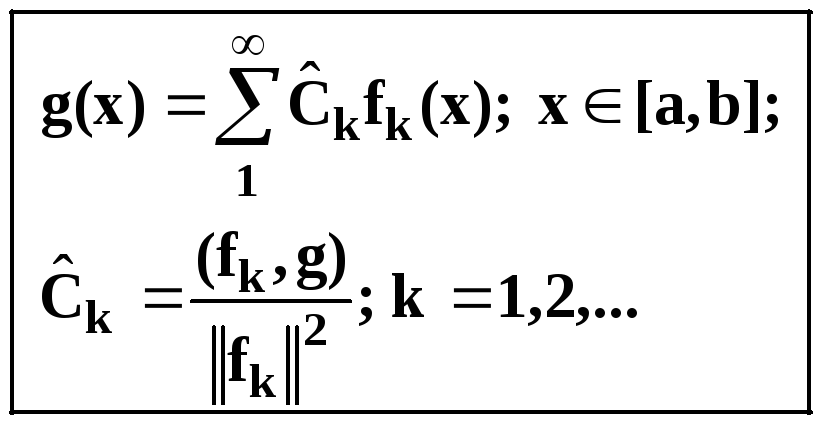называется рядом Фурье для функции g

по ортогональной системе функций F={f₁(x), f₂(x),..,f_k(x),…}. Коэффициенты называются коэффициентами Фурье для функции g по ортогональной системе функций F={f₁(x), f₂(x),..,f_k(x),…}.

Теорию рядов Фурье, примеры ортогональных систем функций, свойства коэффициентов Фурье см., например, в книге «П.К.Суэтин, Классические ортогональные многочлены».

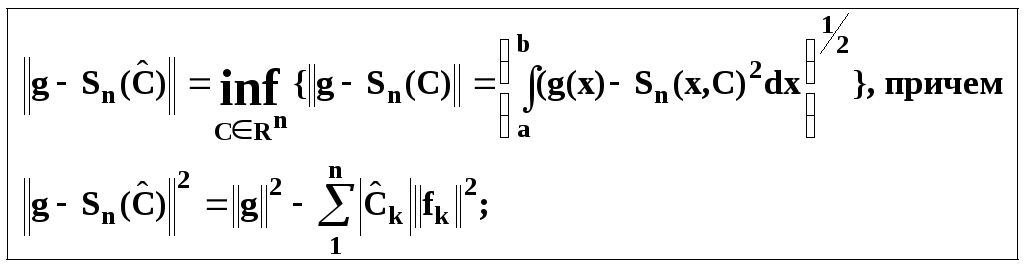
В заключение отметим одно из важных свойств коэффициентов Фурье.

«Многочлен с коэффициентами Фурье (частичная сумма ряда Фурье)

является многочленом наилучшего среднеквадратического приближения функции g по системе функций F={f₁(x), f₂(x),..,f_k(x),…} – этот многочлен минимизирует норму разности