§4 Теорема Дирихле.

Пусть задана функция G: [0;2L]R; G(x) и построен тригонометрический ряд Фурье:

Условия сходимости тригонометрического ряда Фурье и свойства его суммы определяются следующей теоремой, приводимой без док-ва.

Теорема (Дирихле).

«Если функция G(x) кусочно непрерывна на [0;2L], то тригонометрический ряд с коэффициентами Фурье :

[i] сходится на всей числовой оси и определяет на R периодическую функцию S(x) (сумму ряда) с периодом Т=2L: S(x+2Lk)=S(x);

[II] на промежутке [0;2L] ряд сходится к функции G(x) «в среднем» - его сумма S(x)

равна «среднему значению» функции G в точке “x” – полусумме левого и правого пределов функции в точке:

[III] Частичная сумма ряда Фурье является тригонометрическим многочленом наилучшего среднеквадратического приближения функции G(x) на промежутке [0;2L], причем СКО= определяется соотношениями :

В качестве примера построим тригонометрический ряд Фурье для функции g(x)=x²

===========================================================

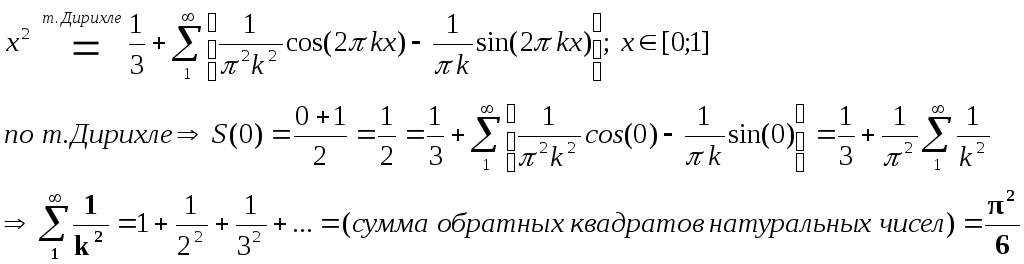
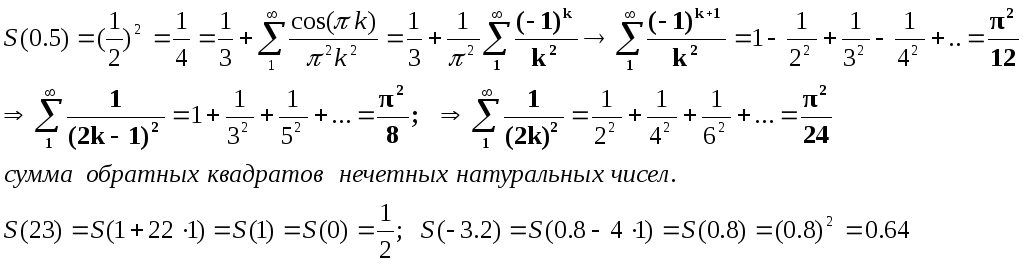
Тр по теме «Ряды Фурье».

Задание.

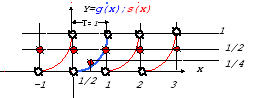
Для заданной графически кусочно-непрерывной на промежутке [0,T] функции G(x)

[I] 1.1Записать «явный вид» функции G(x);

2. Записать тригонометрический ряд Фурье S(x) и изобразить его график на промежутке [-2L;4L].

3. Записать явный вид формул для коэффициентов Фурье А₀,В_0, А _к,В _к.

4. Вычислить с 3 в.з.ц. коэффициенты Фурье для k=0,1,2,3.

5. Записать явный вид тригонометрических многочленов S _k(x);k=0,1,2,3 и вычислить соответствующие им СКО.

[II] 2.1 «Доопределить» функцию G(x) на [-2L;0] как четную или нечетную и выполнить для нее пп.(1.2-1.5)

§5 «Неполные ряды Фурье «по косинусам» и «по синусам».

Пусть функция G: [0,2L]R; G(x) удовлетворяет условиям т. Дирихле.

Ряд Фурье для этой функции имеет вид:

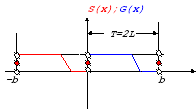
Определим на симметричном промежутке [-2L,2L]R четную и нечетную функции

совпадающие с функцией G(x) на [0,2L].

Разложим эти функции в тригонометрические ряды Фурье на промежутке {-2L;2L]; T=4L,

-b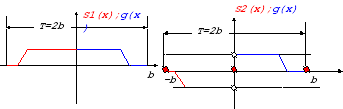

Замечание. Все три ряда Фурье сходятся "в среднем" к функции G(x) на [0,2L].

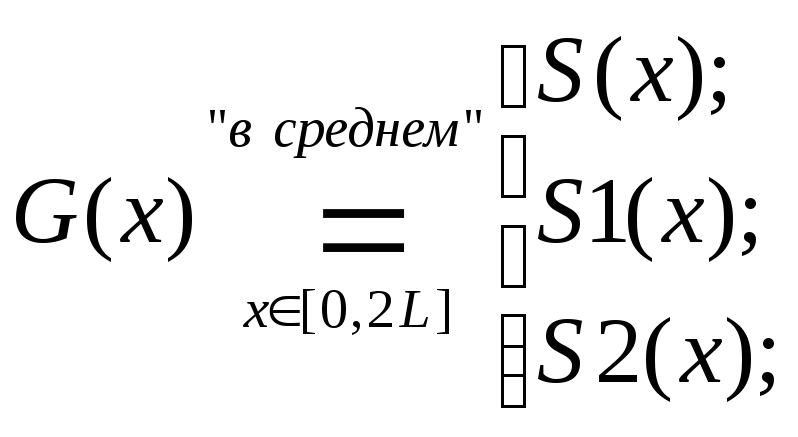
Величина среднеквадратического отклонения приближения функции G(x) соответствующими тригонометрическими многочленоми порядка “n” на промежутке [0;2L]

равны

===================================================================

=======================================================

Разложение функции g(x)=x²; в ряд "по косинусам" имеет вид

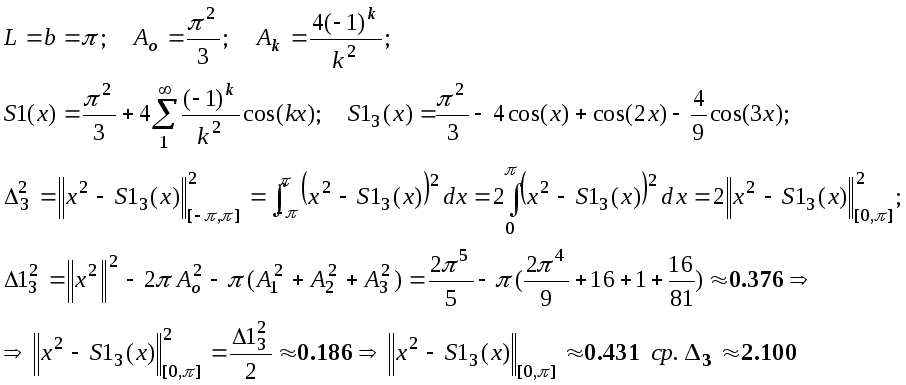
Соответствующее разложение в ряд по синусам имеет вид

===============================================================

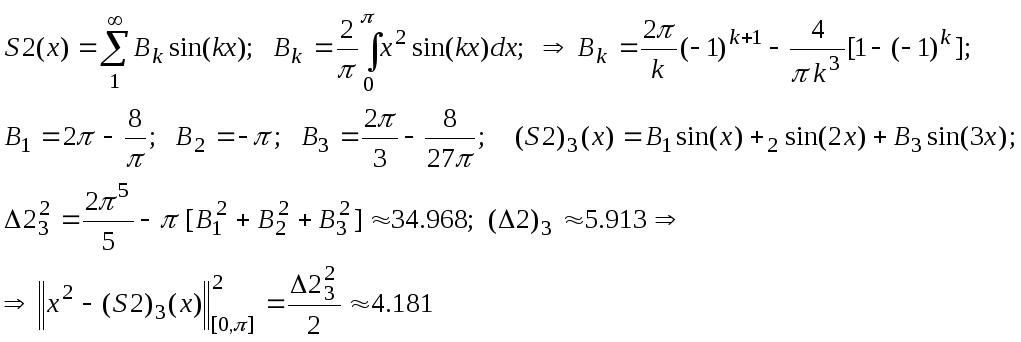
_{Matcad; файл РФ-х^2.mcd}

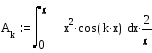
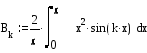
_Bk=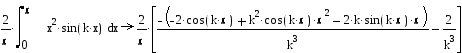

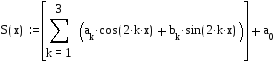
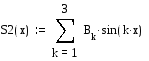
_D3=5.913

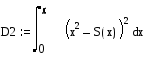
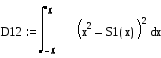
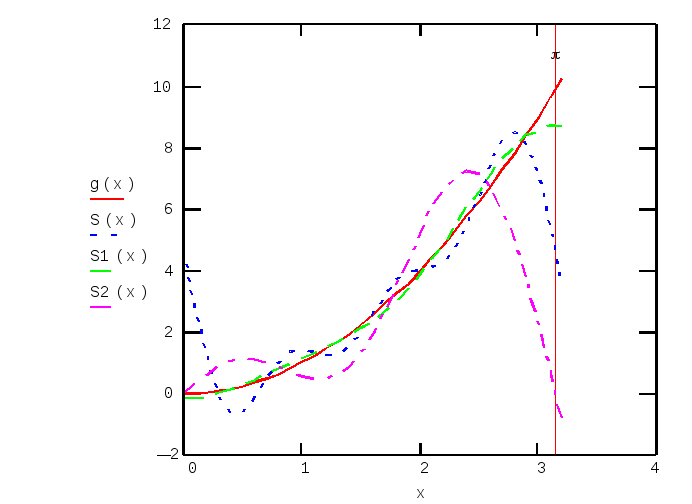
_{Приближение g(x)=x}² _{: полный ряд Фурье  СКО=}

_{Ряд по синусам  СКО= 4.181}

_{Ряд по косинусам  СКО= 0.434}