17

ГЛАВА «Ряды Фурье», ВМ-4 1

§1 Скалярное произведение, норма функций; ортогональная система функций, коэффициенты Фурье. 1

§2 Понятие о ряде Фурье. Многочлен наилучшего среднеквадратического приближения функции. 2

§3 Тригонометрическая система функций. Тригонометрический ряд Фурье. 4

§4 Теорема Дирихле. 6

ТР по теме «Ряды Фурье». 9

§5 «Неполные ряды Фурье «по косинусам» и «по синусам». 9

§5 Постановка задачи приближения функций. Равномерное и среднеквадратическое приближение. 14

Глава «Ряды Фурье», вм-4

«Воспоминания из прошлого и …наводящие соображения».

1)

2)

§1 Скалярное произведение, норма функций; ортогональная система функций, коэффициенты Фурье.

Пусть на промежтке [a,b] задано множество квадратично интегрируемых функций

Опр.1 Скалярным произведением функций называется число, равное интегралу от произведения функций:

Очевидны свойства СП:

1. (f_i,f_k)=(f_k,f_i); 2. (cf_i,f_k)=c(fi_,f_k); 3. (c1f₁+с2f₂,f₃)=c1(f₁,f₃)+c2(f₂,f₃) – скалярное произведение линейной комбинации функций равно линейной комбинации скалярных произведений;

Пример.

Опр.2 Нормой функции, порожденной СП, называется неотрицательное число, равное квадратному корню из интеграла



Свойства нормы.

Опр.3 Две функции называется ортогональными на промежутке, если их СП равно нулю (f_i,f_k)=o. Множество функций F={f_i(x); i=1,2,…} называется ортогональным на промужутке, если его элементы попарно ортогональны : .

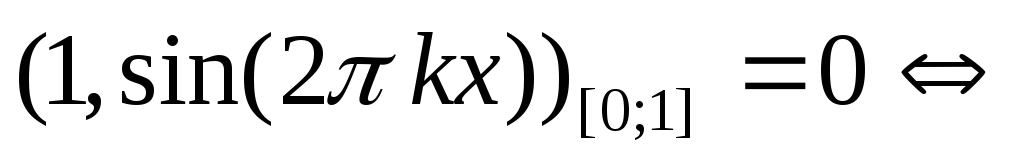• функции ортогональны на [0;1].

• ЭКЗ. : Доказать, что множество функций ортогонально на [0;1].

Пусть функция g: [a,b]R; g(x) квадратично интегрируема на промежутке и множество F={f_i(x); i=1,2,…} – ортогонально на нем.

Опр.4 Числа

(1)

называются коэффициентами Фурье функции g по ортогональной на промежутке системе функций F.



§2 Понятие о ряде Фурье. Многочлен наилучшего среднеквадратического приближения функции.

Рассмотрим бесконечный функциональный ряд с коэффициентами Фурье

Если этот ряд сходится на [a,b], он определяет функцию-сумму ряда

(2)

и называется рядом Фурье для функции g по системе функций F, ортогональной на промежутке.

Системы ортогональных функций, условия сходимости соответствующих рядов Фурье, свойства коэффициентов Фурье рассматриваются в общей теории рядов Фурье, например, И.К.Суэтин, Классические ортогональные полиномы,М., Наука, 1976.

Рассмотрим частичную сумму ряда Фурье и аналогичный многочлен порядка “n” с произвольными коэффициентами :

Теорема (свойство коэффициентов Фурье).

«Во множестве многочленов порядка n с произвольными коэффициентами

}

многочлен с коэффициентами Фурье является многочленом наилучшего среднеквадратического приближения функции g на [a,b], минимизирующим среднее квадратическое отклонение (СКО) многочлена от функции g(x) на промежутке [a;b] – норму разности

==========================================================

ЭКЗ; +1; Доказать теорему, используя :(а)определения нормы функции и коэффициентов Фурье; (б) ортогональность функций (f_i,f_k)=; (в) свойства скалярного произведения и (г) тождество

§3 Тригонометрическая система функций. Тригонометрический ряд Фурье.

Рассмотрим бесконечную систему периодических (Т=1) и попапрно ортогональных на промежутке [0;1] функций

, (1)

квадраты норм которых равны:

Ряд Фурье и его частичная сумма по системе функций F имеют вид:

т (2)

Коэффициенты Фурье для функции g(у); определяются формулами :

(3)

Сренеквадратическое отклонение тригонометрического многочлена S_n(x) от функции g(y) на промежутке [0;1] удовлетворяеет соотношениям:

Замечание.

Если в формулах (1-4) сделать замену переменной , система F отобразится в систему тригонометрических функций

, (1.1),

ортогональных на промежутке [0;2L] и периодических с периодом T=2L :

Квадраты норм этих функций равны:

Ряд Фурье и его частичная сумма для функции G: [0;2L]R; G(x) имеют вид:

Если обозначить то нетрудно показать (выполните это самостоятельно), что коэффициенты рядов (2) и (2.1) равны:

A₀=a₀; A_k=a_k; B_k=b_k; k=1,2,…. (3.1)

Например,

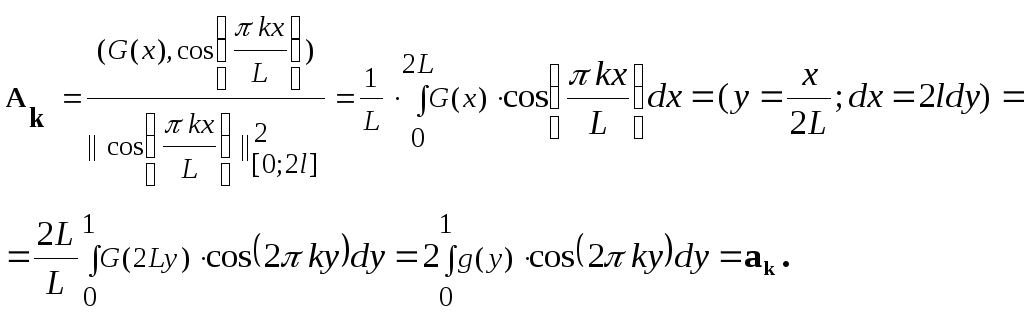
(4.1)