
Методы численного анализа (гэк 2012)
1 Интерполирование функций
Постановка задачи интерполирования
Рассмотрим
на отрезке
![]() некоторую m
– кратно
дифференцируемую функцию
некоторую m
– кратно
дифференцируемую функцию
![]() .
Пусть в
.
Пусть в
![]() точках
точках
![]() известны ее значения
известны ее значения
![]() ,
в
,
в
![]() точках
точках
![]() известны значения первой производной
известны значения первой производной
![]() и в
и в
![]() точках известны значения m
–ой производной
точках известны значения m
–ой производной
![]() .
Значения функции и ее производных
называются данными
интерполирования,
а точки
.
Значения функции и ее производных
называются данными
интерполирования,
а точки
![]() – узлами
интерполирования.
– узлами
интерполирования.
Задача
интерполирования
заключается в отыскании функции
![]() из некоторого класса
из некоторого класса
![]() такой, что выполняется условие
такой, что выполняется условие
![]() .
(1.1)
.
(1.1)
Пусть
![]() .
Рассмотрим на отрезке
последовательность линейно независимых
m
– кратно
дифференцируемых функций:
.
Рассмотрим на отрезке
последовательность линейно независимых
m
– кратно
дифференцируемых функций:
![]() .
В качестве семейства
возьмем всевозможные линейные комбинации
первых
.
В качестве семейства
возьмем всевозможные линейные комбинации
первых
![]() функций с произвольными коэффициентами
функций с произвольными коэффициентами
![]() .
.
Из условия (1.1)
получим систему линейных алгебраических
уравнений для определения коэффициентов
![]()
![]() . (1.2)
. (1.2)
Система (1.2) будет иметь единственное решение в том случае, если ее определитель отличен от нуля.
Примеры интерполяционных функций
Приведем примеры интерполяционных функций.
1. Рассмотрим
следующую систему линейно независимых
функций:
![]() .
Тогда семейством
является совокупность алгебраических
многочленов вида
.
Тогда семейством
является совокупность алгебраических
многочленов вида
![]() .
(1.3)
.
(1.3)
Геометрически
это означает, что нужно найти алгебраическую
кривую
![]() ,
проходящую через систему точек
,
проходящую через систему точек
![]() (Рисунок 1.1).
(Рисунок 1.1).
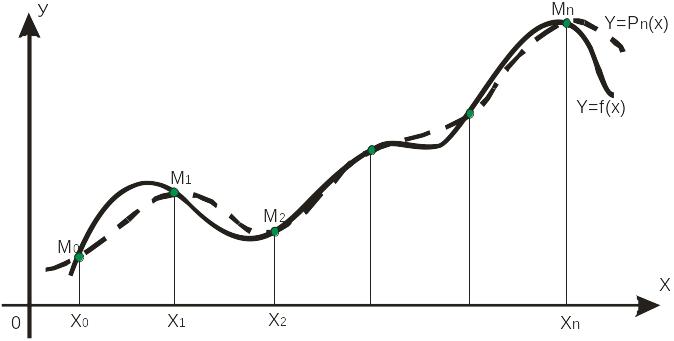
Рисунок 1.1 – Интерполяционный многочлен
Система уравнений,
из которой определяются коэффициенты
![]() из (1.3), будет
из (1.3), будет
![]() .
(1.4)
.
(1.4)
Ее определитель
является определителем Вандермонда, и
он отличен от нуля для различных между
собой значениях
![]() .
.
Интерполирование полиномами вида (1.3) называется алгебраическим.
2. Для интерполирования
периодических функций с периодом
![]() применяется система тригонометрических
функций:
применяется система тригонометрических
функций:
![]() .
Линейная комбинация первых
.
Линейная комбинация первых
![]() функций является тригонометрическим
многочленом степени
функций является тригонометрическим
многочленом степени
![]() . (1.5)
. (1.5)
Интерполирование с помощью полиномов (1.5) называется тригонометрическим.
Пусть для функции
построена интерполирующая функция
.
Тогда, если определяется значение
в точке
![]() ,
лежащей внутри отрезка
интерполирования, то такое восстановление
функции называется интерполяцией.
Если же точка
лежит вне отрезка
,
то такое восстановление функции
называется экстраполяцией.
,
лежащей внутри отрезка
интерполирования, то такое восстановление
функции называется интерполяцией.
Если же точка
лежит вне отрезка
,
то такое восстановление функции
называется экстраполяцией.
Конечные разности и их свойства
Конечные разности в вычислительной математике имеют значение, аналогичное дифференциалам в анализе бесконечно малых величин.
Пусть даны
равноотстоящие друг от друга узлы
![]() и известны соответствующие значения
функции
и известны соответствующие значения
функции
![]() .
Здесь
.
Здесь
![]() – некоторое фиксированное значение
аргумента.
– некоторое фиксированное значение
аргумента.
Конечными
разностями
нулевого
порядка
называются величины
![]() равные
значениям функции
равные
значениям функции
![]() в узлах
в узлах
![]() .
Конечными разностями первого
порядка называются величины
.
Конечными разностями первого
порядка называются величины
![]() (1.6)
(1.6)
Конечные разности второго порядка определяются равенствами по отношению к разностям первого порядка
![]()
Разности n-го порядка определяются по формуле
![]() .
(1.7)
.
(1.7)
Конечные разности любого порядка легко выражаются через значения функции
![]() (1.8)
(1.8)
Доказательство
проведем по индукции. Пусть эта формула
верна для
![]() .
Покажем, что она будет верна и при
.
Покажем, что она будет верна и при
![]() .
.
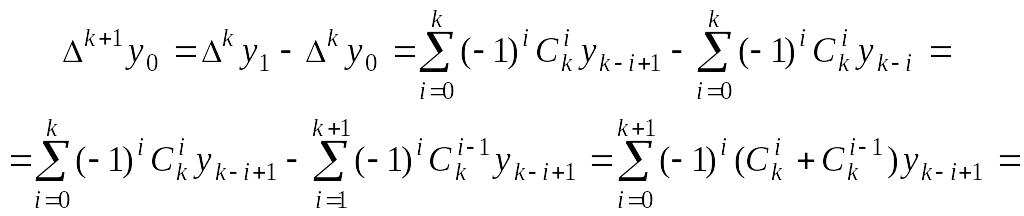
![]()
![]()
![]() .
.
Аналогично доказывается формула
![]() (1.9)
(1.9)
Из определения конечных разностей вытекают следующие свойства
если
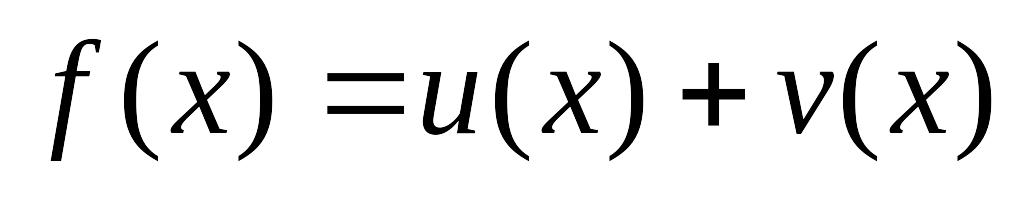 ,
то
,
то
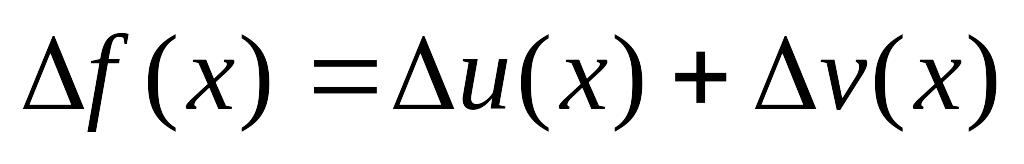 ;
;если
 ,
,
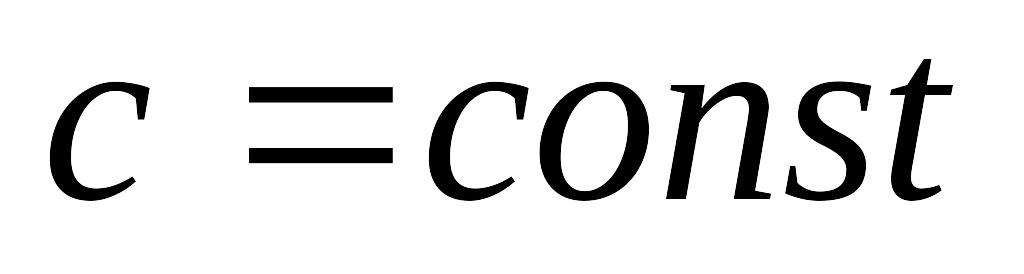 ,
то
,
то
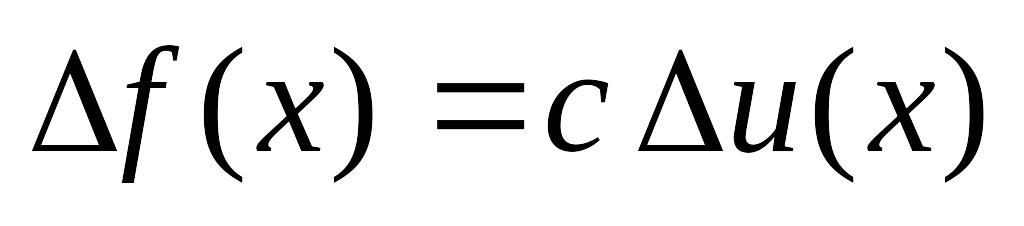 ;
;конечные разности n –го порядка от многочлена степени n постоянны
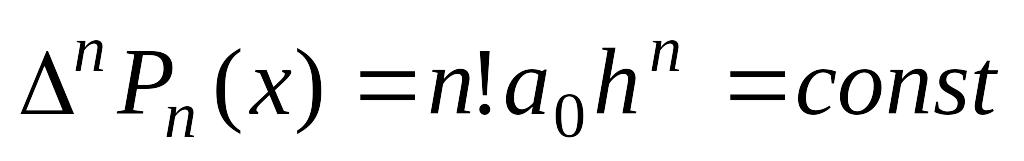 ,
а
,
а
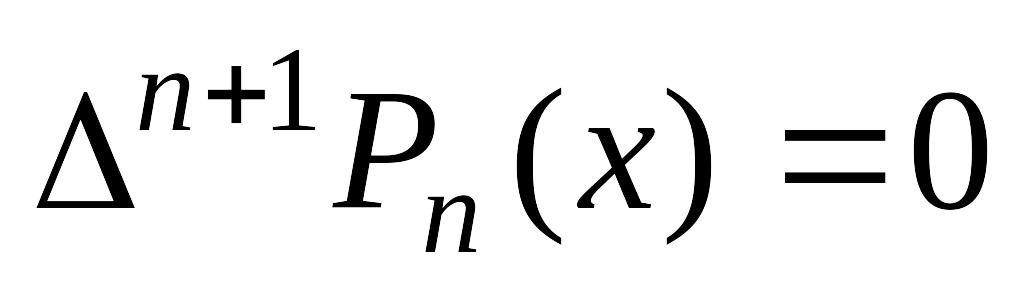 ;
;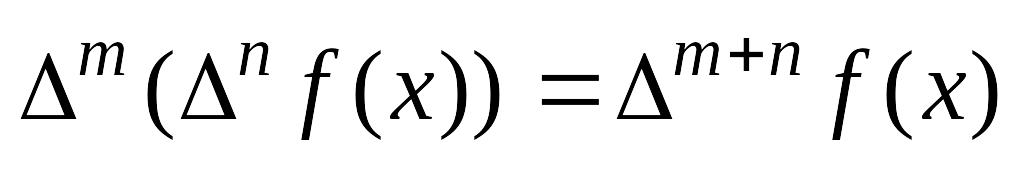 .
.
Таблицу конечных разностей обычно располагают следующим образом:
Таблица 1.1 – Конечные разности
x |
|
|
|
|
|
|
|
x0 |
f0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
f1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
f2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
f3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 |
f4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x5 |
f5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x6 |
f6 |
|
|
|
|
|
|
Теорема о существовании интерполяционного многочлена
Пусть
на отрезке
![]() в
в
![]() узле
узле
![]() заданы значения ограниченной функции
:
заданы значения ограниченной функции
:
![]() .
Поставим задачу нахождения полинома
.
Поставим задачу нахождения полинома
![]() степени не выше
такого, чтобы выполнялось условие
степени не выше
такого, чтобы выполнялось условие
![]() .
(1.10)
.
(1.10)
Теорема 1.
Существует и притом единственный
многочлен степени не выше
![]() ,
для которого выполняется условие (1.10).
,
для которого выполняется условие (1.10).
Доказательство.
Пусть многочлен
имеет вид (1.3). Используя (1.10), для
определения коэффициентов
![]() ,
получим систему (1.4) линейных алгебраических
уравнений, которую запишем в виде
,
получим систему (1.4) линейных алгебраических
уравнений, которую запишем в виде
![]()
![]()
. . . . . . . . . . . . . . . . . . . . . . . . (1.11)
![]()
Определитель системы (1.11) является определителем Вандермонда и имеет вид
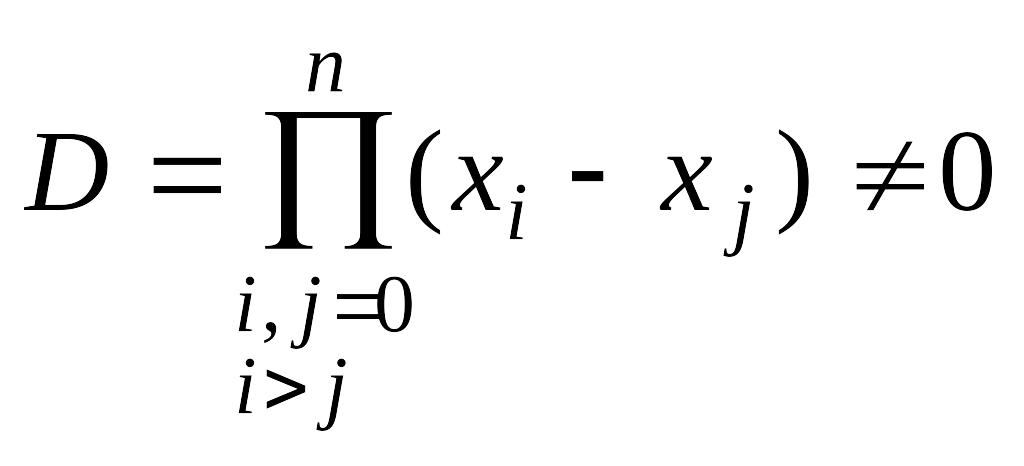 .
.
Следовательно, для системы различных между собой узлов система (1.11) имеет единственное решение. Теорема доказана.
