Лабораторная работа 6 / Lab6

Кафедра МО ЭВМ

ОТЧЕТ

по лабораторной работе № 6 по дисциплине

"Методы оптимизации"

“ Задача о коммивояжере ”

Выполнили: Воробьёв А.В.

Ламеров Д.Ю.

Швецов М.Н.

Шефер Е.В.

Факультет КТИ

Группа № 4352

Проверил Балтрашевич В.Э.

«Выполнено» «____» _______ ____

Подпись преподавателя __ _

Санкт-Петербург

2006

Цель работы

Изучение метода ветвей и границ на примере реше­ния задачи коммивояжера.

Постановка задачи

Коммивояжер должен побывать в каждом из n городов в точности по одному разу и закончить свое путешествие в том городе, откуда он его начал. Задача коммивояжера состоит в минимизации суммарных дорожных расходов.

Формально она может быть поставлена так:

Минимизировать

при условиях

(6.1)

(6.2)

перестановка

(6.3)

где (i₁, j₁), ..., (i_n, j_n) - индексы ненулевых переменных X_ij

не содержит внутренних циклов.

Здесь

C_ij - стоимость переезда из i-го города в j-й,

1, если путь из i-го города j-й включается в марш-

X_ij = ­рут коммивояжера,

О, иначе.

Краткие общие сведения

Поставленная задача очень напоминает задачу о назначениях и отличается от последней лишь наличием дополнительного условия (6.3). Это обстоятельство, однако, делает ее нелинейной и не позволяет применить к ее решению методы линейного программирования (служащие, в частности, базой классического "венгерского" метода решения за­дачи о назначениях). Тем не менее, задача коммивояжера может ус­пешно решаться с помощью весьма общего метода решения переборных задач - метода ветвей и границ.

Напомним здесь основную идею метода. Конечное множество реше­ний задачи последовательно разбивается на подмножества, на каждом из которых вычисляется оценка снизу минимизируемой функции.

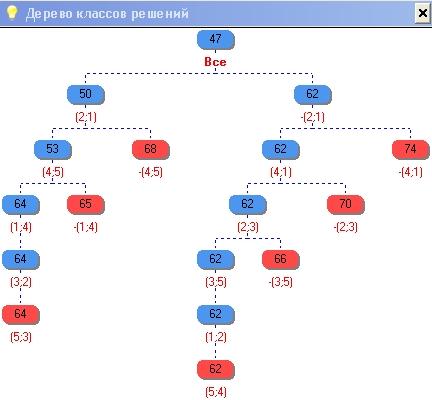
Процесс последовательного деления через конечное число шагов приводит к появлению подмножества, содержащего всего одно решение. Для такого подмножества оценка снизу целевой функции может быть заменена ее точным значением, которое объявляется так называемым "рекордом". С момента появления "рекорда" появляется возможность сравнивать с ним "потенциальные возможности", заложенные в каждом из получившихся подмножеств:

а) если оценка снизу целевой функции на каком-либо подмножест­ве больше, чем "рекорд", то соответствующее подмножество можно ис­ключить из дальнейшего рассмотрения;

б) если в процессе разобщения выявляется одноточечное подмно­жество (решение), для которого значение целевой дикции меньше, чем "рекорд", то старое "рекордное" решение заменяется новым.

Процесс разбиения на подмножества удобно фиксировать в виде дерева, вершины которого соответствуют подмножествам.

Описанная выше общая схема будет работоспособной только в том случае, если конкретизировать в ней два ключевых момента:

а) способ выбора очередного подмножества, подлежащего разбие­нию, и правило, по которому оно осуществляется.

б) метод получения оценки.

1. Правило разбиения:

а) любое подмножество разбивается на две части;

б) одна из частей содержит все маршруты, входящие в разбивае­мое подмножество и включающие путь, связывающий два конкретных го­рода; вторая часть является дополнением первой и соответственно содержит маршруты, в которых движение по выбранному пути запрещено;

в) правило выбора упомянутого пути будет приведено ниже.

2. Способ получения оценки снизу стоимости маршрутов, входящих в подмножество.

Подмножество маршрутов удобно кодировать с помощью пары:

а) (i⁽¹⁾,j⁽¹⁾), ..., (i^(l),j^(l)) - набора путей, включаемых во все маршруты подмножества;

б) матрицы вида:

	j1		jn-l+1
i1	C'i1,j1		C'i1,jn-l+1
...	...
in-l+1	C'in-l+1,j1	...	C'in-l+1,jn-l+1

Здесь {i₁,i₂,...,i_n-l+1} = {1,2,...,n} \ {i⁽¹⁾,i⁽²⁾,...,i^(l)} - номера городов, для которых в рамках данного подмножества остается откры­тым вопрос о том, куда из них двигаться; аналогичный смысл имеет множество {j₁,j₂,...,j_n-l+1}. Числа C'_ip,jq - это модифицированные стоимости переездов (см.ниже). Некоторые из них могут быть равны бесконечности, что означает запрет движения по соответствующим путям.

Способ получения оценки стоимости, а заодно и выбора пути, по которому проводится разбиение, поясним на примере разбиения исход­ного (полного) множества маршрутов.

1. Редуцировать матрицу стоимостей, т.е. последовательно вы­честь из каждой строки ее минимальный элемент, после чего осущест­вить ту же процедуру применительно к столбцам. Сумма вычитаемых в процессе редукции чисел Х – редукционная сумма - даст искомую оценку.

2. Для каждого из нулевых элементов редуцированной матрицы С'_ij вычислить

3. Осуществить разбиение по тому пути, для которого величина Δ_ij максимальна.

4. В подмножестве маршрутов, исключающих путь (i, j), соответствующую стоимость положить равной бесконечности и провести редукцию по i-й строке и j-му столбцу. Сумма X + Δ_ij даст оценку снизу.

5. В подмножестве маршрутов, включающих путь (i, j), осуществить следующую последовательность действий:

а) вычеркнуть элементы i -й строки и j -го столбца;

б) найти путь, движение по которому может привести к образова­нию внутреннего цикла, и положить его стоимость равной бесконечности (в простейшем случае, в частности, при разбиении исходного мно­жества, - это путь (j, i));

в) провести редукцию получившейся матрицы;

г) добавить редукционную сумму к X и получить оценку снизу для рассматриваемого подмножества.

Отметим, что разбиение любого подмножества, кроме исходного, выполняется по приведенному выше алгоритму, начиная со 2-го пункта.

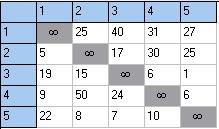
Вариант

	1	2	3	4	5
1		25	40	31	27
2	5		17	30	25
3	19	15		6	1
4	9	50	24		6
5	22	8	7	10	

Испытание метода

Исходная матрица:

Сокращённая матрица расстояний с оценкой нулей:

Выбираем дугу: (2, 1); штраф: 15; исключаем дугу: (1, 2). Результаты исследований:

Выбираем дугу: (4, 5); штраф: 18; исключаем дугу: (5, 4). Результаты исследований:

Выбираем дугу: (1, 4); штраф: 12; исключаем дугу: (5, 2). Результаты исследований:

Выбираем дугу: (3, 2); штраф: ; исключаем дугу: (5, 3). Результаты исследований:

Матрица показывающая текущий маршрут:

Вернёмся на второй уровень дерева классов решений:

Выбираем дугу: (4, 1); штраф: 12; исключаем дугу: (1, 4). Результаты исследований:

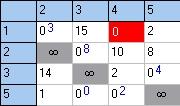
Выбираем дугу: (2, 3); штраф: 8; исключаем дугу: (3, 2). Результаты исследований:

Выбираем дугу: (3, 5); штраф: 4; исключаем дугу: (5, 2). Результаты исследований:

Выбираем дугу: (1, 2); штраф: ; исключаем дугу: (5, 4). Результаты исследований:

Матрица показывающая текущий маршрут:

Текущая оценка стоимости является минимальной среди альтернативных, следовательно, текущий маршрут является оптимальным, то есть решением данной задачи:

Дерево классов решений: