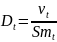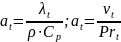- •1. Понятие об основных и производных, первичных и вторичных единицах измерения. Формула размерности.
- •3. Жидкости и газы. Ньютоновская и неньютоновская жидкости. Закон реологической связи напряжений и скоростей деформаций.
- •4. Понятие о физических свойствах сплошных сред. Изотропия и анизотропия.
- •7. Уравнение подобия. Определяемые и определяющие критерии и числа подобия.
- •16. Определение вихревой диффузии и вихревой теплопроводности в рамках статистического метода.
- •17. Метод преобразования координат в решении задач гидродинамики (роль пристеночных эффектов и точность их расчета)
- •18. Понятие о диффузионных задачах Дирихле и Неймана.
- •19. Понятие о численных и аналитических решениях задач гидродинамики, сравнительный анализ и погрешности расчета интегральных параметров течения и теплообмена.
16. Определение вихревой диффузии и вихревой теплопроводности в рамках статистического метода.
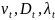 - турбулентные
(вихревые) коэффициенты переноса:
коэффициент турбулентной кинематической
вязкости, коэффициент турбулентной
диффузии, коэффициент турбулентной
теплопроводности.
- турбулентные
(вихревые) коэффициенты переноса:
коэффициент турбулентной кинематической
вязкости, коэффициент турбулентной
диффузии, коэффициент турбулентной
теплопроводности.
При осреднении уравнений Навье-Стокса по Рейнольдсу появляется дополнительный член вида u’v’, который принято называть Рейнольдсовым напряжением и который отличает ламинарное движение от турбулентного (в ламинарном этого члена нет). Величину данной двойной корреляции пульсационных величин принято искать в рамках различных гипотез, одной из которых является гипотеза Буссинеска о турбулентной вязкости:
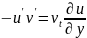 в которой одна
неизвестная величина u’v’,
по сути, заменяется другой неизвестной
величиной, турбулентной вязкостью. То
есть введение этих коэффициентов в
рамках феноменологического метода и
представлений о сдвиговом течении среды
переносит проблему определения
турбулентных пульсаций на проблему
определения коэффициента vt.
в которой одна
неизвестная величина u’v’,
по сути, заменяется другой неизвестной
величиной, турбулентной вязкостью. То
есть введение этих коэффициентов в
рамках феноменологического метода и
представлений о сдвиговом течении среды
переносит проблему определения
турбулентных пульсаций на проблему
определения коэффициента vt.
Аналогично, записывают соотношения для коэффициентов турбулентной диффузии и теплопроводности:
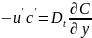 и
и
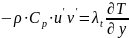 .
.
В
соответствие с современными представлениями
и гипотезами, точность определения
турбулентных коэффициентов связана
только с точностью определения поля
скоростей. Турбулентную вязкость
выражают с помощью модифицированной
формулы Колмогорова-Прандля:
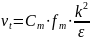 .
.
Остальные турбулентные коэффициенты выражают с помощью аналогии процессов переноса импульса и тепла, импульса и массы, следующим образом:
|
|
Smt и Prt - константы, их значение составляет 0,9. Однако они являются константой только в ядре потока. В пограничном слое их значение резко меняется. |
17. Метод преобразования координат в решении задач гидродинамики (роль пристеночных эффектов и точность их расчета)
В пристеночном слое для различных величин (скорость, температура, концентрация) всегда наблюдается область высоких градиентов, оказывающая значительное влияние на закономерности течения по всему сечению канала.
В задачах о сложном сдвиговом течении при движении в каналах с переменной формой поперечного сечения (например, конфузоры / диффузоры), при движении химически реагирующих смесей, вращающихся потоков активизируются процессы диффузии (импульса, тепла, массы) - усиливаются мелкомасштабные эффекты, увеличиваются градиенты параметров.
Для их точного определения необходимо использовать априорную и апостериорную (то есть до и после опыта) информацию о всех вихревых движениях - и с этой целью в определяющих уравнениях, описываюзих течение и тепломассоперенос, вводиться ЗАМЕНА ПЕРЕМЕННЫХ, которая обеспечивает сгущение координатных линий в особых областях сгущения - например, в зоне стенки, входа, рециркуляции, отрыва, присоединения потока. Таким образом, так как мы сгущаем сетку в нужных нам местах, мы гарантированно «захватываем» расчетной сеткой мелкомасштабные эффекты и не теряем их в расчете.
Сама замена переменных представляет собой переход от, например, системы координат {X; Y} в систему координат {X’; η} следующей заменой:
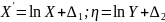
 где
Δ1 и Δ2 называются «параметрами сгущения».
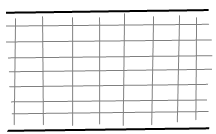
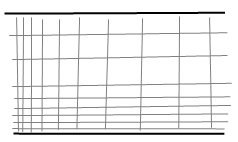
Таким образом, обеспечивается следующий
переход (рис ниже). Использование сгущения
по логарифмическому закону наиболее
удачно, поскольку распределение скоростей
при турбулентном течении в трубопроводе
также подчиняется логарифмическому
закону.
где
Δ1 и Δ2 называются «параметрами сгущения».
Таким образом, обеспечивается следующий
переход (рис ниже). Использование сгущения
по логарифмическому закону наиболее
удачно, поскольку распределение скоростей
при турбулентном течении в трубопроводе
также подчиняется логарифмическому
закону.
|
|
Равномерная сетка. |
Сетка со сгущением на входе и на нижней стенке. |