
- •1. Понятие об основных и производных, первичных и вторичных единицах измерения. Формула размерности.
- •3. Жидкости и газы. Ньютоновская и неньютоновская жидкости. Закон реологической связи напряжений и скоростей деформаций.
- •4. Понятие о физических свойствах сплошных сред. Изотропия и анизотропия.
- •7. Уравнение подобия. Определяемые и определяющие критерии и числа подобия.
- •16. Определение вихревой диффузии и вихревой теплопроводности в рамках статистического метода.
- •17. Метод преобразования координат в решении задач гидродинамики (роль пристеночных эффектов и точность их расчета)
- •18. Понятие о диффузионных задачах Дирихле и Неймана.
- •19. Понятие о численных и аналитических решениях задач гидродинамики, сравнительный анализ и погрешности расчета интегральных параметров течения и теплообмена.
1. Понятие об основных и производных, первичных и вторичных единицах измерения. Формула размерности.
Единицы измерения, вводимые с помощью эталонов, которым, по определению, присваивается числовое значение, равное единице, называются основными единицами измерения.
Единицы измерения величин, которые получаются из основных единиц измерения с помощью соответствующих физических законов или из определений этих величин, называются производными единицами измерения.
Основные единицы системы СИ: метр – единица длины, килограмм – единица массы, кельвин – единица температуры,
|
кандела – единица сила света, ампер – единица силы тока, секунда – единица времени, моль – количество вещества.
|
Дополнительные единицы: радиан- единица плоского угла, стерадиан - единица телесного угла.
Под внесистемными единицами понимают единицы, которые не входят в какую-либо систему единиц. Примерами таких единиц могут быть ангстрем, центнер, литр, калория и др
Исходным пунктом для вывода формулы размерности является утверждение, что внутри заданного класса все системы единиц измерения равноправны. Отсюда следует, что отношение двух численных значений какой-либо производной величины не зависит от выбора масштабов основных единиц измерения внутри данного класса систем единиц измерения. Например:

Т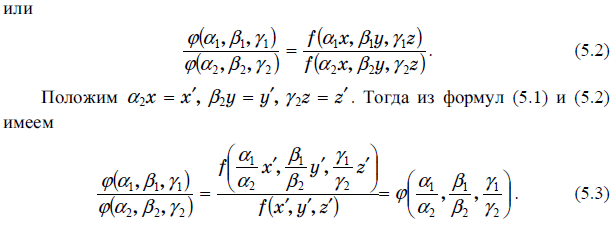
 аким
образом,
доказано,
что
формула размерности физической величины
имеет вид степенного одночлена.
аким
образом,
доказано,
что
формула размерности физической величины
имеет вид степенного одночлена.
Из формулы (5.7) следует, что для безразмерных величин m = n = l = 0, ϕ=1.
2. Понятие о сжимаемых и несжимаемых сплошных средах.
Сжимаемость - свойство жидкости изменять свой объем под действием давления. Сжимаемость жидкостей характеризуется коэффициентом объемного сжатия βр, который выражает относительное изменение объема жидкости V0, отнесенное к единице давления p и определяется по формуле
βр=(-dV/V0)·(1/dp),
Знак минус в формуле обусловлен тем, что положительному приращению давления соответствует отрицательное приращение (уменьшение) объема. Единицы измерения βр в системе МКГСС — м2/кгс, в системе СИ - 1/Па. Часто βр выражается в см2/кгс.
Если принять, что приращение давления dp=p-р0, а изменение объема dV=V-V0, то
V= V0·(1- βр·dp), ρ=ρ0/(1- βр·dp),
где V и V0 - объемы, а ρ и ρ0 - плотности соответственно при давлениях p и р0
Жидкость
называется несжимаемой,
если плотность любой ее частицы есть
величина постоянная, то есть если
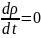 .
.
Вследствие малости изменения объема под действием давления (для воды коэф. сжимаемости = 0,000049), при решении дифференциальных уравнений капельные жидкости принято считать несжимаемыми, а для газов используют специальных критерий - число Маха, связанный со скоростью звука в данной среде.
Ч![]() исло
Маха, где
исло
Маха, где
![]() —
скорость потока, а
—
скорость потока, а
![]() —
местная скорость звука,
—
местная скорость звука,
является мерой влияния сжимаемости среды в потоке данной скорости на его поведение: из уравнения состояния идеального газа следует, что относительное изменение плотности (при постоянной температуре) пропорционально изменению давления:
![]()
из
закона Бернулли разность давлений в
потоке
![]() ,
то есть относительное изменение
плотности:
,
то есть относительное изменение
плотности:
![]()
Поскольку
скорость звука
![]() ,
то относительное изменение плотности
в газовом потоке пропорционально
квадрату числа Маха:
,
то относительное изменение плотности
в газовом потоке пропорционально
квадрату числа Маха:
![]()
Таким образом, если число Маха порядка единицы, то сжимаемость газообразных сред необходимо учитывать.
