
3. Единственность решения.
Пусть
существует два решения
 и
и
 задачи (2) – (7). Тогда их разность
задачи (2) – (7). Тогда их разность
 удовлетворяет тому же уравнению (1), но
с правой частью
удовлетворяет тому же уравнению (1), но
с правой частью
 ,
и однородным граничным условиям:
,
и однородным граничным условиям:
 ,
,
 .
(76)
.
(76)
Введем в рассмотрение функции:
 ,
(77)
,
(77)
 ,
(78)
,
(78)
 .
(79)
.
(79)
Продифференцируем равенства (77)–(79) по переменной получим


 ,
(80)
,
(80)

 ,
(81)
,
(81)
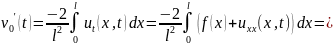
 .
(82)
.
(82)
Проинтегрируем дважды по частям в равенствах (80)–(82) получим

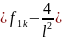


 ,
,



 ,
,
 ,
,
где
 ,
,
 ,
,
 .
(83)
.
(83)
Итак, равенства (73)–(75) равносильны следующим дифференциальным уравнениям
 ,
(84)
,
(84)
 ,
(85)
,
(85)
 ,
(86)
,
(86)
Для функций (70) –(72) на основании (69) имеем граничные условия:
 ,
,
 ,
(87)
,
(87)
 ,
,
 ,
(88)
,
(88)

 .
(89)
.
(89)
Проинтегрируем уравнение (84) по переменной , получим
 ,
,
где
 произвольная постоянная.
произвольная постоянная.
Функция
 должна удовлетворять граничным условиям
(89) т.е.
должна удовлетворять граничным условиям
(89) т.е.


Итак, получили, что
 .
(90)
.
(90)
Решение
дифференциального уравнения (85) будем
искать методом Бернулли. Пусть
 .
Тогда
.
Тогда
 Подставив выражение функции, и ее
производной в уравнение (85) получим:
Подставив выражение функции, и ее
производной в уравнение (85) получим:

 (91)
(91)
Будем
считать, что функция
такова, что
 Решим полученное дифференциальное
уравнение первого порядка с разделяющимися
переменными. Разделим переменные
Решим полученное дифференциальное
уравнение первого порядка с разделяющимися
переменными. Разделим переменные
 ,
,
 .
.
Получили дифференциальное уравнение с разделенными переменными. Продифференцируем полученное равенство, получим
 ,
,
 ,
,

где
 – произвольная постоянная.
– произвольная постоянная.
Полученная
функция
является общим решением уравнения.
Положим
 ,
тогда функция
примет вид
,
тогда функция
примет вид
 .
.
Тогда уравнение (91) примет вид:

Так как при любых , то разделим левую и правую часть уравнения на выражение . Получим уравнение
 .
.
Отсюда получаем

Из
предположения, а так же из равенств для
 и
и
 получаем, что искомая функция имеет
вид:
получаем, что искомая функция имеет
вид:
 (92)
(92)
где произвольная постоянная.
Функции
вида (92) должны удовлетворять граничному
условию (88). Следовательно, коэффициенты
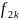 и
определяются из системы
и
определяются из системы


Определитель полученной системы равен
 ,
.
,
.
Итак,
у не однородной системы определитель
отличен от
 ,
следовательно, система имеет единственное
нулевое решение. То есть
,
следовательно, система имеет единственное
нулевое решение. То есть
 ,
,
 ,
а следовательно
,
а следовательно
 .
(93)
.
(93)
С учетом равенства (93) дифференциальное уравнение (86) принимает вид
. (94)
Аналогично получаем, что дифференциальное уравнение второго порядка (94) с граничными условиями (80) имеет решение вида
. (95)
Из равенств (77)–(79) и (83) имеем:
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
.
,
.
Отсюда
в силу полноты системы функций (39) в
пространстве
следует, что
 почти всюду на
почти всюду на
 при любом
при любом
 и
и
 почти всюду на
почти всюду на
 .
В силу (2), (3) функция
.
В силу (2), (3) функция
 непрерывна в
непрерывна в
 и
и
 ,
поэтому
,
поэтому
 в
и
в
и
 на
.
на
.
Итак, получаем


Следовательно, наше предположение не верно.
Теорема 1. Если существует решение задачи (2)–(7), то оно единственно.
