2.2. Построение квазиоптимального фильтра

Построение оптимального фильтра не всегда возможно, поэтому строят фильтр, близкий по отношению сигнал/помеха к оптимальному, называемый квазиоптимальным.

Ухудшение отношения сигнал/помеха на выходе квазиоптимального фильтра по сравнению с оптимальным равно:

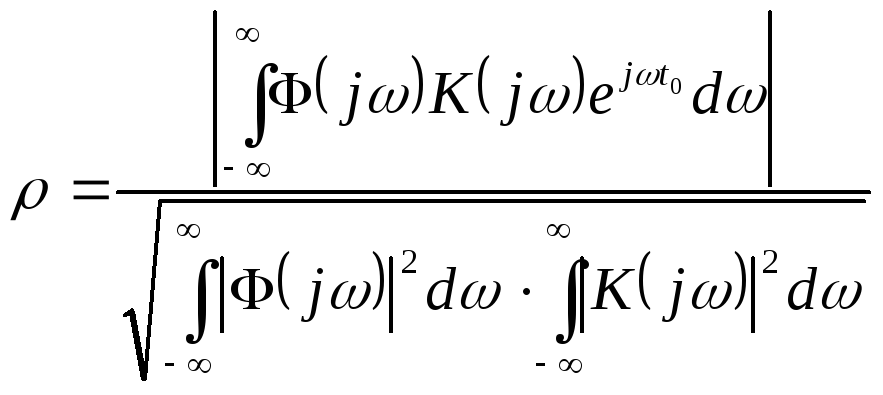
По условию квазиоптимальный фильтр состоит из 4 несвязанных колебательных контуров. Тогда его передаточная функция равна:

Обозначим – полуширина спектра сигнала, – полуширина полосы пропускания фильтра.

Найдем полосу пропускания из условия, что , а ширину спектра из условия

Преобразуя функцию для , получим числитель:

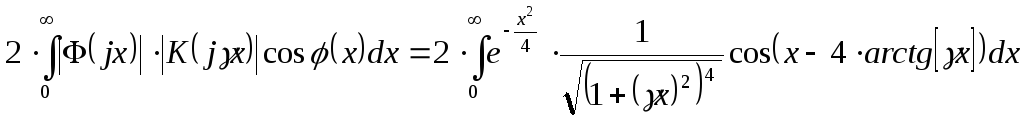
Знаменатель равен:

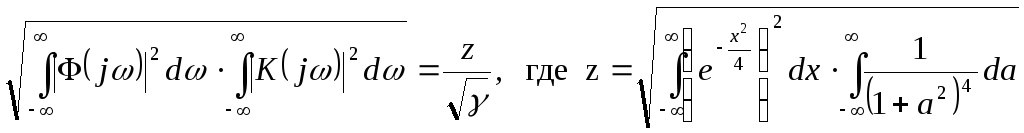
Отношение сигнал/помеха на выходе квазиоптимального фильтра выражается через отношение сигнал/помеха на его вхо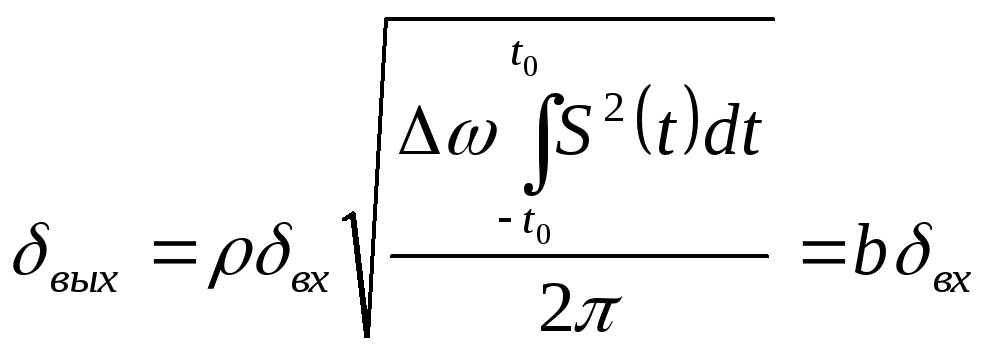де:

, где

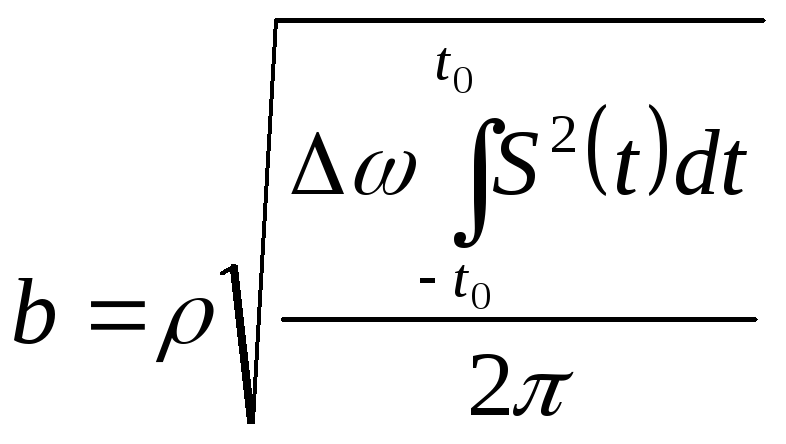
С учетом выше сказанного произведем расчет в MathCad данных характеристик

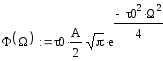
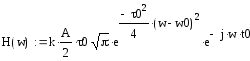
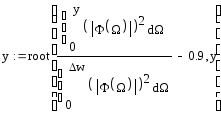
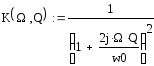
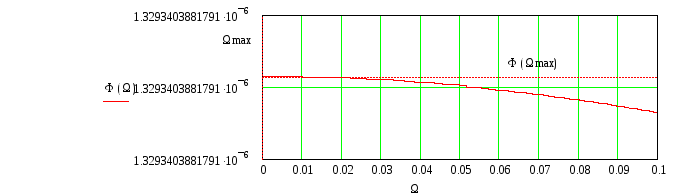
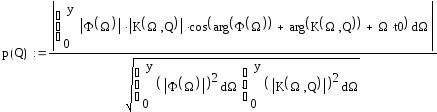
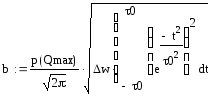
3. Определение характеристик обнаружения Обнаружитель состоит из следующих блоков:

1. Согласованный фильтр

2. Линейный детектор

3. И нтегратор

4. Пороговое устройство

Вероятность правильного обнаружения сигнала для простейшего обнаружителя Неймана–Пирсона равна: ,где – отношение дисперсий сигнала и шума.

Вероятность перебраковки , где в числителе стоит среднее количество ложных регистраций, а в знаменателе – число независимых точек контроля.

Среднее количество ложных регистраций определяется из трансцендентного уравнения: , где в нашем случае .

Для обнаружителя выполненного по данной схеме справедливо выражение:

.

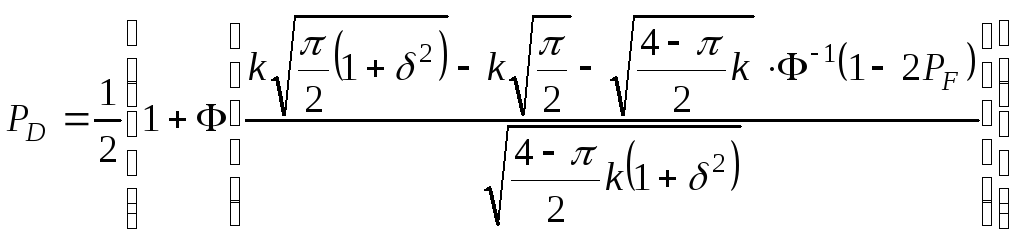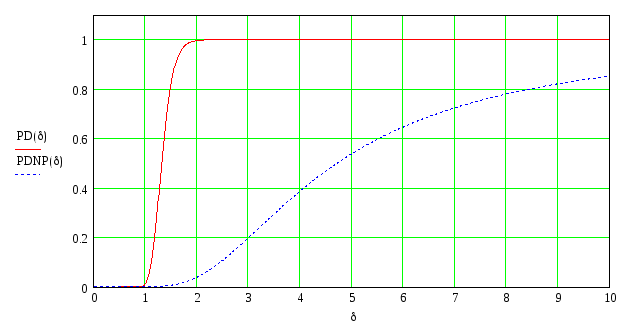
Кривая для данного фильтра и простейшего фильтра Неймана – Пирсона

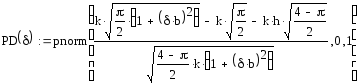
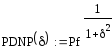
3. Выводы

В результате выполнения курсовой работы было выполнено:

1. Определена частотная характеристика и на основании принципа практической реализуемости построен оптимальный фильтр.

2. Определены параметры квазиоптимального фильтра: ширина полосы пропускания фильтра 1.095МГц и отношение сигнал/помеха на его выходе по сравнению с входом .

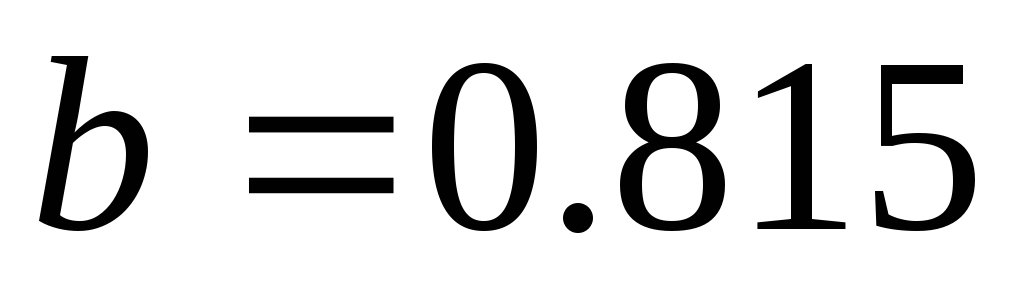3. Получена зависимость вероятности правильного обнаружения от отношения сигнал/помеха на входе приемного тракта. Для сравнения приведена аналогичная зависимость для работы простейшего обнаружителя Неймана – Пирсона.