Определение точки пересечения прямой и плоскости

Пусть прямая L задана каноническими уравнениями:

,

плоскость P – общим уравнением

.

 . Найти точку .

Чтобы найти точку необходимо решить систему уравнений

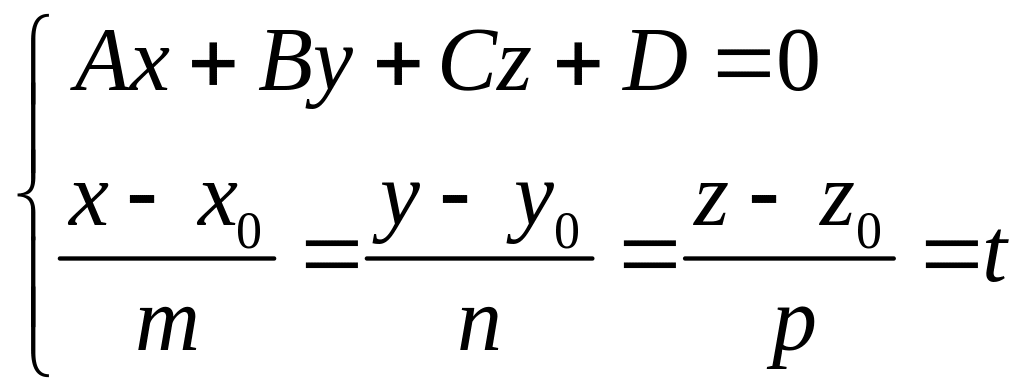. (6.8)

Точку пересечения прямой и плоскости удобнее находить, если прямая задана параметрическими уравнениями. Тогда параметр t для точки легко определяется из системы линейных уравнений:

.

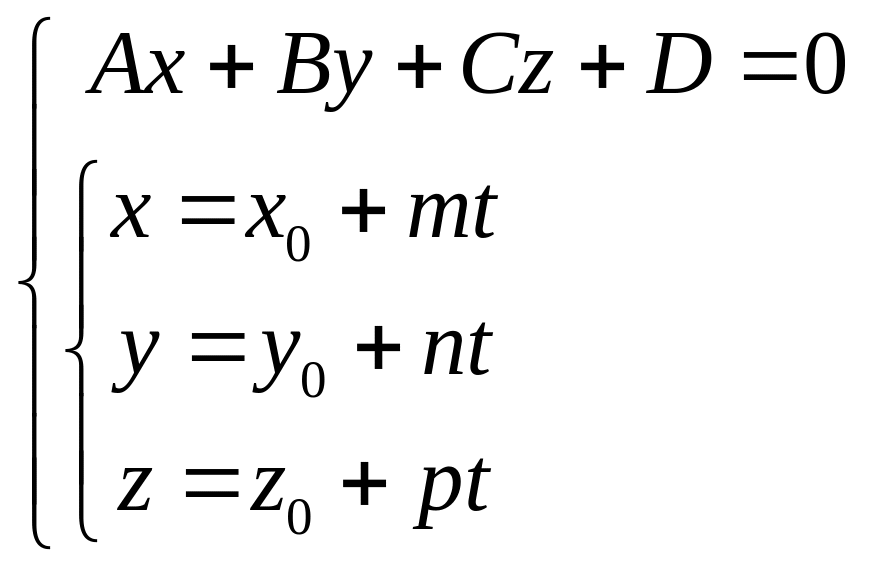Угол между прямой и плоскостью

Таким образом, углом между прямой L и плоскостью P можно найти по следующей формуле

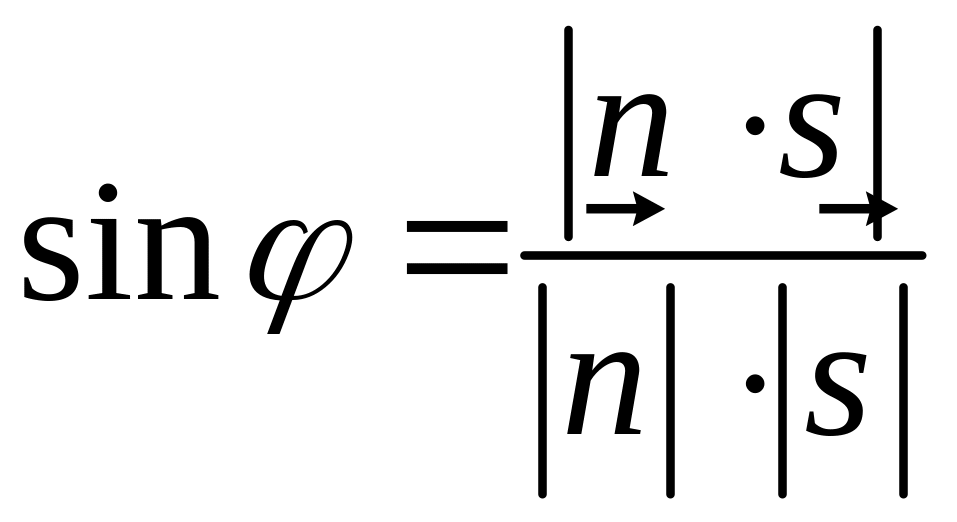. (6.9)

7. Поверхности второго порядка

Определение 7.1. Поверхностью второго порядка называют поверхность, которая задана алгебраическим уравнением второй степени

, (7.1)

где не все коэффициенты при членах второго порядка одновременно равны нулю.

Может оказаться, что уравнение (7.1) определяет так называемую вырожденную поверхность (пустое множество, точку, плоскость, пару плоскостей, прямую). Если же поверхность невырожденная, то преобразованием декартовой прямоугольной системы координат ее уравнение может быть приведено к одному из указанных ниже видов, называемых каноническими и определяющих тип поверхности.

Прежде чем перейти к каноническим уравнениям поверхностей второго порядка, остановимся на типах поверхностей, которые характеризуются способом построения. По способу построения поверхностей в пространстве выделяют три основных типа:

1) цилиндрические поверхности;

2) поверхности вращения;

3) конические поверхности.

Поверхность, образованная движением прямой L, которая перемещается в пространстве, сохраняя постоянное направление и пересекая каждый раз некоторую кривую K, называется цилиндрической поверхностью или цилиндром.

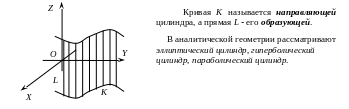
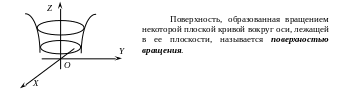
7.1. Канонические уравнения и поверхности второго порядка

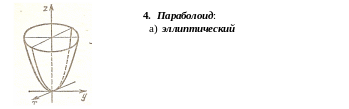
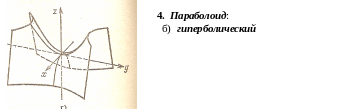
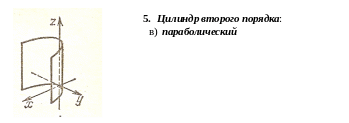
Форма и свойства всех перечисленных выше поверхностей второго порядка устанавливаются с помощью метода параллельных сечений. Суть метода состоит в том, что поверхности пересекаются плоскостями, параллельными координатным плоскостям, а затем по виду и свойствам получаемых в сечениях линий делается вывод о форме и свойствах самой поверхности.